一种二阶常系数非齐次线性微分方程特解的设定方法
倪臣敏,管典安
(华侨大学厦门工学院数学教研室,福建厦门 361021)
二阶常系数线性微分(差分)方程的内容,在现行的高等数学或者经济数学(微积分)中主要介绍了两种类型的求解,即齐次的(1)和非齐次的(2),

这两种类型的方程无论在工程应用模型还是经济分析模型的建立中都有非常重要的基础性作用。根据线性微分方程解的结构定理[1],二阶常系数非齐次线性微分方程(2)的解为y=Y+y*。其中Y为其对应的齐次方程(1)的通解,y*为(2)的一个特解。Y易用特征方程法,快速而简便地求解。特解y*的求法较为复杂,一般是采用待定系数法[1],即先设出y*的形式,再将其代入原方程(2),根据等式两边同类项前的系数对应相等,解出待定系数。
在众多高等数学或者微积分教材中,特解y*的设定都是经过简单推导后,分类给出设定公式,如高等数学[1]中,对于于f(x)=eλxPm(x)(其中Pm(x)为m次多项式)的情形,给出(2)的特解形式y*是:
y*=xkQm(x)eλx,其中Qm(x)为m次多项式,

y*=xkeλx,其中为m次多项式。

如何用统一的方法,给出特解的形式,有很积极的研究意义。本文就常见高等数学教材中f(x)的两种类型f(x)=eλxPm(x)及f(x)=eλx,根据其导数的特点,给出了新的特解y*的设定法,此方法统一了(3)和(4)两个结论,亦适用于一二阶常系数非齐次线性差分方程特解的设定求解。
1 主要内容
1.1 对非齐次项的分析
考察f(x)的两种类型,各阶导数的特点。
(i)若f(x)=eλxPm(x),则
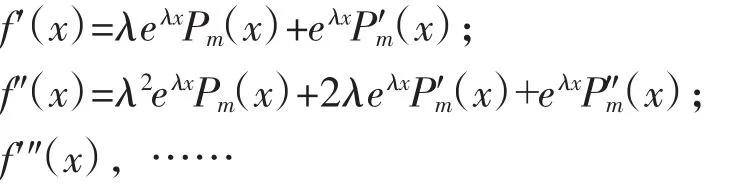
因Pm(x)的m+1阶导数为0,且(eλx)(n)=λneλx,故f(x)的各阶导数展开式中,所含同类项为有限项。如f(x)=(x2+1)e2x,f′(x)=2xe2x+2(x2+1)e2x=2(x2e2x+xe2x+e2x),继续求f″(x),f′″(x),…。f(x)的各阶导数所含同类只有三项x2e2x,xe2x和e2x,而f(x)是其中两个同类项的线性组合f(x)=x2e2x+e2x。
(ii)若f(x)=eλx[P1l(x)cosωx+P2n(x)sinωx],由于正弦和余弦函数导数的交互性,不难推导出f(x)的各阶导数中所含同类项的个数也是有限的。事实上,应用欧拉公式,亦可以将此f(x)化为指数和多项式相乘的类型。
1.2 特解的设定方法
定理 设二阶常系数非齐次线性微分方程
y″+py′+qy=f(x)(f(x)=eλxPm(x)或f(x)=eλx对应的齐次方程的通解为Y=C1g1(x)+C2g2(x)且f(x),f′(x),f″(x)…所含同类项为有限项,则上述非齐次方程特解的待定形式为

证明仅就f(x)=eλxPm(x)且m=2时,作简要证明,其他情况略。设此时对应齐次方程的通解为Y。
当m=2时,f(x)=eλx(a2x2+a1x+a0),容易求出f(x),f′(x),f″(x)…所含同类项为x2eλx,xeλx,eλx三项,故原方程的特解初步设定为y*=ax2eλx+bxeλx+ceλx=(ax2+bx+c)eλx。
(i)若y*与Y中无相同的同类项,则说明λ不是特征方程的特征根,由(3)y*的待定形式为:y*=ax2eλx+bxeλx+ceλx=(ax2+bx+c)eλx。
(ii)若y*与Y中有相同的同类项,则说明λ是特征方程的特征根,若为单根,则y*x与Y无相同的同类项,故特解的待定形式为x(ax2+bx+c)eλx;若为重根,则y*x与Y中仍有相同的同类项,y*x2与Y中无相同的同类项,故原方程特解的待定形式为:x2(ax2+bx+c)eλx。
显然,上述特解形式等同于引言中(3)式给出的结论。
需要注意的是,本定理中特解形式的设定是基于非齐次项f(x)及其各阶导数所含的同类项的有限性,其假设的关键是保证特解形式和对应齐次方程的通解不含相同的同类项。
例1 写出下列微分方程特解的待定形式。
(i)y″-3y′+2y=2x+3;(ii)y″-3y′+2y=xe2x;(iii)y″-3y′+2y=excos2x.
解:容易看出(i)~(iii)对应的齐次方程的通解均为Y=C1ex+C2e2x,Y中所含同类项为ex,e2x.
对于(i),f(x)=2x+3,f′(x)=2,f″(x)=f′″(x)=…=0,f(x)及其各阶导数所含同类项为x和常数项,他们都和Y中所含的同类项不同,故(i)方程的特解的待定形式为y*=ax+b(其中a,b为任意常数)。利用引言中(3)式结论验证之,因f(x)=2x+3=e0x(2x+3),0不是特征方程r2-3r+2=0的根,故(i)特解的待定形式为y*=ax+b(其中a,b为任意常数)。
对于(ii),非齐次项f(x)=xe2x,f(x)及其各阶导数所含同类项为xe2x和e2x,有与Y中所含的同类项相同的项e2x,故原方程的特解待定形式初步设定为(axe2x+be2x)x,此特解形式中所含同类项为x2e2x和xe2x,它们与Y中所含的同类项均不相同,故方程(ii)特解的待定形式设为y*=(axe2x+be2x)x(其中a,b为任意常数)。同理可用(3)式结论验证之。
对于(iii),非齐次项f(x)=excos2x,f(x)及其各阶导数所含同类项为有限项excos2x和exsin2x,且均与ex,e2x不相同,故其特解的待定形式为y*=aexcos2x+bexsin2x(其中a,b为任意常数)。利用引言(4)式容易验证此结论的正确性。
从以上解题过程可以看出,本文介绍的方法使得两种非齐次项的类型特解的设定得到了统一,而且简单直观,为后续的方程求解提供了很大的方便。
对于非齐次项为定理中的两种情况相加的情形,需根据叠加原理[1]来获得微分方程的特解形式。
例2 求y″+y=ex+cosx的特解的待定形式。
解 考虑方程y″+y=ex和y″+y=cosx,分别求出其对应的特解的待定形式y*1=aex和y*2=bcosx+csinx,由叠加原理,所求方程的特解待定形式为y*=aex+bcosx+csinx。
事实上,对于例2方程的求解,较简便的方法是:先将y*1,y*2分别代入其对应的方程,解出待定系数a,b,c,获得非齐次方程的一个特解,再根据解的结构定理写出其通解。
2 结论的拓展
可以验证文中的定理所介绍的方法同样适用于对一二阶常系数非齐次线性差分方程特解的求解。例3 求下列方程的一个特解。
(i)yx+1+yx=x·2x;(ii)yx+2+3yx+1-4yx=-2.
解(i)对应齐次方程的通解[2]为Yx=C(-1)x。非齐次项为f(x)=x·2x,f(x)及其各阶导数所含同类项为2x,x·2x,且均与Yx所含的同类项(-1)x不同,故方程(i)特解的待定形式可设为,从而b(x+1)·2x+1,将,代入方程(i)得,这就求得方程(i)的一个特解
(ii)对应齐次方程的通解为Yx=C1(1)x+C2(-4)x=C1+C2(-4)x,所含同类项为(-4)x和常数项。非齐次项为f(x)=-2,f(x)及其各阶导数所含同类项为常数项,与Yx中所含的一个同类项相同,故其特解形式设为(此时所含同类项x与Yx中所含的两个均不相同),将(x+1)代入方程(ii)得,即得方程(ii)的一个特解
[1]同济大学数学系.高等数学[M].6版.北京:高等教育出版社,2007.
[2]吴传生.经济数学——微积分[M].2版.北京:高等教育出版社,2009.
[3]朱德刚.二阶常系数线性微分方程的特解公式[J].高等数学研究,2010,13(3):15-16.

