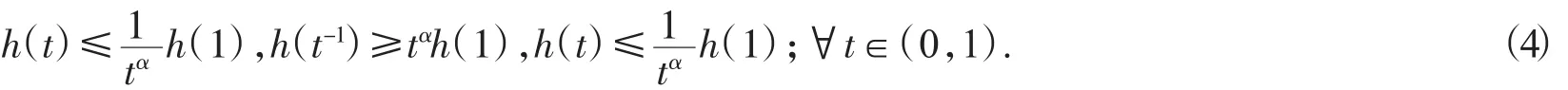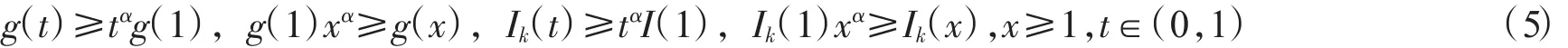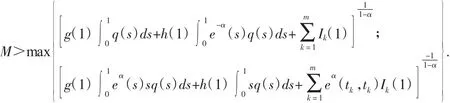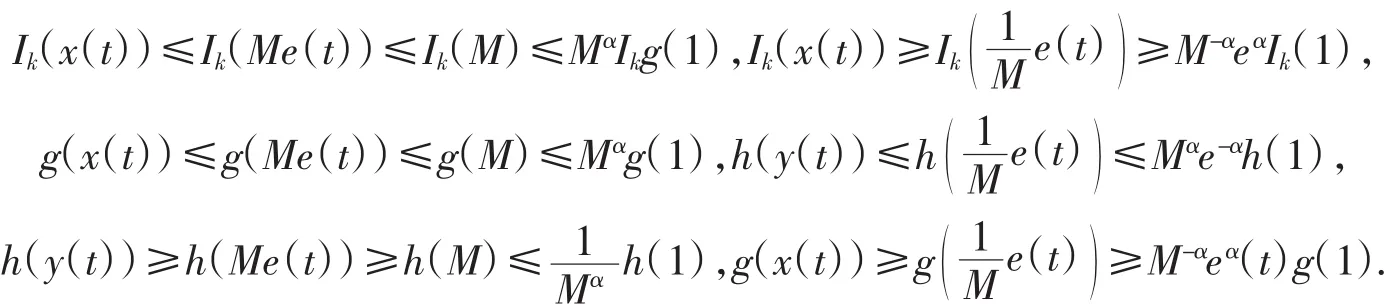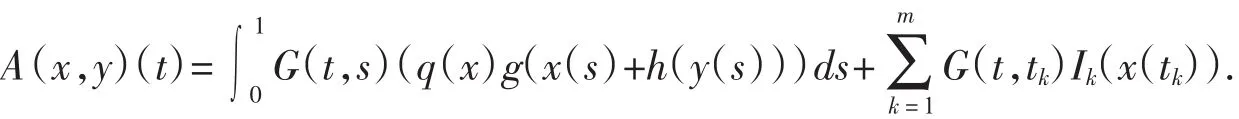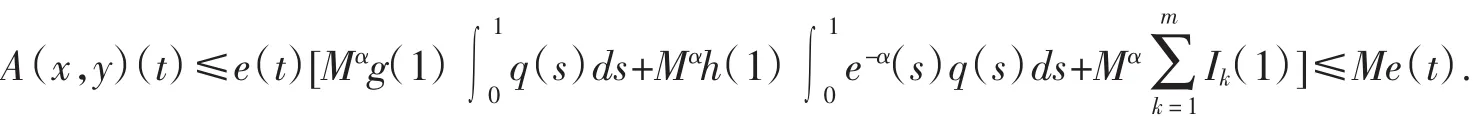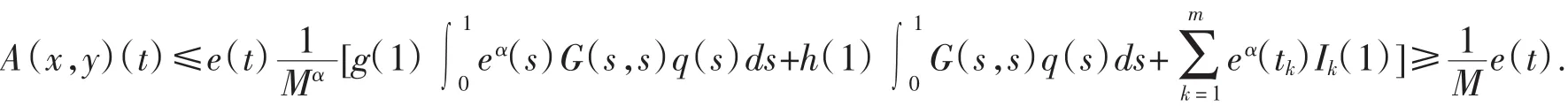二阶脉冲微分方程混合边值正解的存在唯一性
汤 宇
(吉林工商学院基础部,吉林长春 130062)
本文利用格林函数,将微分方程转化成等阶解的积分方程,研究奇异脉冲微分方程二点混合边值问题

这里0 本文根据混合单调算子的不动点定理,考虑奇异脉冲微分方程(1),约定f(t,u)=q(t)(g(u)+h(u)),t∈(0,1),并且g∶[0,∞)→[0,∞),g(y)是连续递增的函数,h∶(0,∞)→(0,∞),h(y)是连续递减的函数。 令P是Bananch空间E的一个正规锥,并且e∈P,||e||≤1,e≠θ,定义 定义1.1[4]假定A:Qe×Qe→Qe。称A是混合单调算子,如果A对于x是递增的,而对于y是递减的,即对任何y∈Qe,如果x1≤x2,((x1,x2)∈Qe),则 A(x1,y)≤A(x2,y),对任何x∈Qe,如果y1≤y2,((y1,y2)≤Qe),则A(x,y1)≥A(x,y2),称y*是 A 的一个不动点,如果A(y*,y*)=y*. 定理1.1[4]假定A:Qe×Qe→Qe是混合单调算子,并且存在一个常数α∈(0,1),使得坌x,y∈Qe,t∈(0,1)成立,则A存在唯一不动点 x*∈Qe,此外,对坌(x0,y0)∈Qe×Qe,xn=A(xn-1,yn-1),yn=A(yn-1,x n-1),xn→x*,yn→x*,其中||xn-x*||=莓(1-ra),||yn-x*||=莓(1-ra),r是一个与(x0,y0)有关的常数。 用 G(t,s)表示边值问题,-u″(t)=0,u(0)=0,0 容易验证 G(t,s)有不等式 G(t,s)≤t,G(t,s)≤s,ts≤G(t,s)成立。 引理2.1 方程(1)有正解当且仅当积分方程 定理2.1 假如存在0<α<1,使得 对任意的t∈(0,1),y>0都成立,并且 q∈C((0,1),(0,∞)),满足则方程(1)存在唯一的正解y*λ。 证明 根据条件(2)令 t-1y=x,则 h(x)≥tαh(tx),因此令 x=1,则有 同理,根据条件(3)可以得到结论 从条件(7)~(8),对任意的x,y∈Qe,有 对任意 x,y∈Qe,t∈[0,1],定义 首先说明A:Qe×Qe→Qe,对任何 x,y∈Qe,由(6)有 再由(6)有 因此A是一个好的定义,并且 A(Qe×Qe)∈Qe。另外,对任何 I∈(0,1),x,y∈Qe,有 所以根据定理1.1,方程(1)存在唯一解y*∈Qe使得A(y*,y*)=y*,并且y*是方程的唯一正解。类似地,可以证明下面定理。 定理2.2假如存在0<ɑ<1,使得h(t-1y)≥tαh(y),Ik(t-1y)≥tαIk(y),g(ty)≥tαg(y)对任意的t∈(0,1),y>0都成立,并且 q∈C((0,1),(0,∞))满足则方程(1)存在唯一的正解y*。 [1]LakshmikanthamV,BainovDD,SimeonovP S.Theoryofimpulsive differential equations[M].Singapore:World Scientific,1989. [2]苑成军,文香丹.奇异二阶连续和离散边值问题正解的存在唯一性[J].数学的实践与认识,2008(19):173-180. [3]苑成军,文香丹.奇异四阶P-Lapacian微分方程边值正解的存在唯一性[J].黑龙江大学自然科学学报,2009,26(2):173-180. [4]郭大钧.非线性分析中的序方法[M].济南:山东科技出版社,2000.1 预备知识
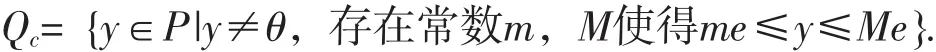
2 主要结论