Logistic回归模型分析应用

蔡俊娟

（厦门海洋职业技术学院基础部，福建厦门 361000）

广义线性模型描述一个响应变量的均值与一个自变量的关系，这个关系可以比线性模型中EYi=α+βx复杂得多。很多不同的模型可以表示为GLM，有一种非常有用的GLM就是Logistic回归模型。Logistic回归分析是一种非常有效的处理数据的方法，特别是在医学、社会调查等领域被广泛应用。但是在现有的统计教科书中，一般都只有对Logistic回归模型的简单介绍，并作为中心内容，缺乏有关该模型的详尽分析及深入的讨论。其中文献[3]只对理论部分进行分析，未结合实际应用案例进行解释说明。

1 模型推导[1]

假设响应变量Y1，Y2，…，Yn是独立的，并且Yi·Bernoulli（πi）。我们知道Bernoulli是指数分布族，再假设πi满足

从而我们建立了πi与x之间的关系。在(1)式中，左边是Yi成功胜率的对数。这个模型假定对数胜率是预测变量x的线性函数。那么Bernoulli概率密度函数可以写成如下的指数形式：

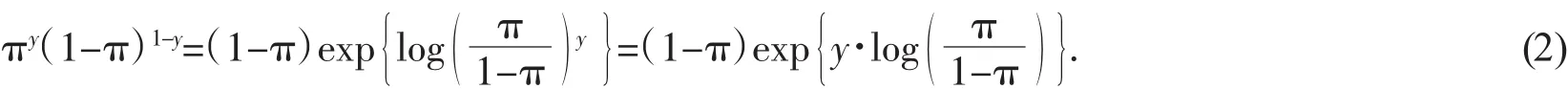
对于方程(1)式，我们可以重新写为:

或者是更一般的形式：

2 模型性质

2.1 单调性

由于

所以，从式(5)中我们可以发现，当β是正数时，π（x）严格递增函数；当β是负数时，π（x）严格递减函数；特别地，β是0时，，则为简单的线性回归模型。

2.2 对称性

2.3 优比

我们可以计算一下在x和x+1处可以得到：对于任何x，

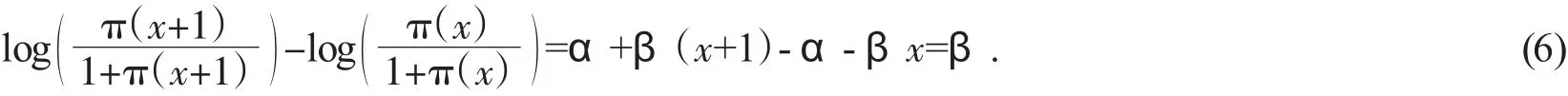
则β表示是当x增加一个单位时，成功的对数胜率的相应变化。在简单线性回归模型中，β是当x增加一个单位时，Y的均值的相能变化。接下来，将式(5)两边取指数可以得到：，也就是说，eβ是指x+1处成功的胜率相对于x处成功的胜率的优比，也可以理解为相应于x的单位增量的成功胜率的变化倍数。

3 抢救急性心肌梗死病人能否成功的危险案例

3.1 案例描述

在研究医院抢救急性心肌梗死(AMI)病人能否成功的危险因素调查中，某医院收集了5年里该院所有AMI病人的抢救病史，共190例。其中Y=0表示抢救成功，Y=1表示抢救未能成功而死亡；x1=1表示抢救前已发生休克，x1=0表示抢救前未发生过休克；x2=1表示抢救前发生心力衰竭，x2=0表示抢救前未发生心力衰竭；x3=1表示病人从开始AMI症状到抢救时已超过12小时（即未能及时把病人送往医院），x3=0表示病人从有AMI症状到抢救时未超过12小时。

表1 抢救急性心肌梗死病人能否成功数据表

3.2 本案例的Logistic回归分析结果

利用SPSS软件，对于上述数据进行分析。

3.2.1 模型系数的综合检验

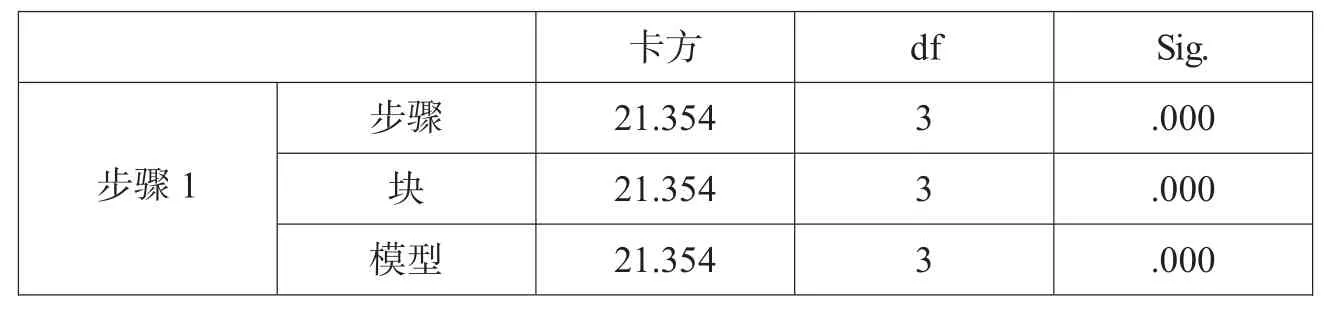
表2 模型系数的综合检验

从表2中，可以发现：模型χ2=21，354，p=0.000＜0.1,按α=0.05水准，认为自变量x1(抢救前是否发生休克)，x2(抢救前是否心力衰竭)，与因变量P(是否抢救成功)的Logistic回归方程有统计学意义。

2.2.2 分类表从表3可以得到，结局为“0”，即抢救成功的患者正确率为90.7%，结局为“1”，即抢救不成功的患者判断正确率为25%。对建模数据总的回判正确率真为69.8%，这说明模型的预测效果是相当不错的，说明该模型较为稳定，尤其是对抢救成功的患者的预测。

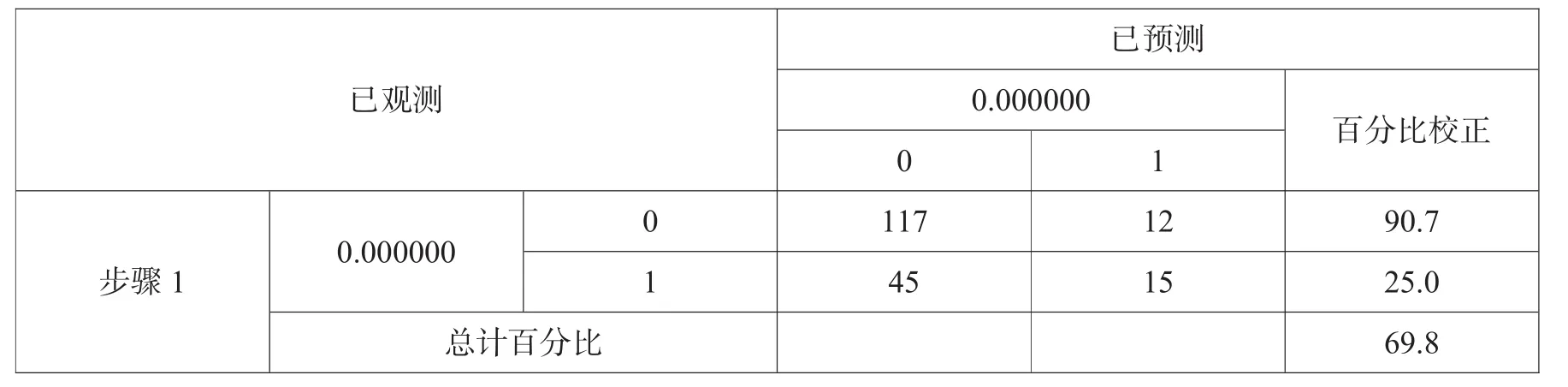
表3 分类表a

2.2.3 方程中的变量

表4 方程中的变量

从表4可以发现：x1、x2、x3的Wald值分别为13.356、2.764、5.180，但是再观察这3个变量的P值，x1的P值为0.000(P<0.01)，从而可以得到，按水准α=0.05水准，x1与Y有显著性关系；x2的P值为0.096(P>0.05)，从而可以得到，按α=0.05水准，x2与Y有无显著性关系；x3的P值为0.023(P<0.05)，从而可以得到，按α=0.05水准，x3与Y有显著性关系。3个因素所建立的Logistic回归方程如下：

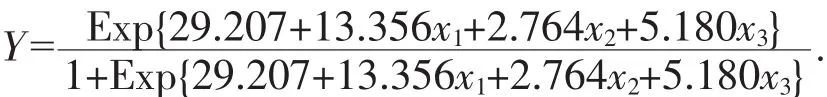
3 结语

通过二项Logistic回归分析可以得到结论，医院抢救急性心肌梗死(AMI)患者能否成功与该患者抢救前是否发生休克以及该患者在抢救时是否已超过12小时是显著相关的。从而，在今后的AMI抢救中，要及时将患者送往医院，这是影响抢救效果的重要因素。

[1]George,Casella.统计推断[M].2版.北京:机械工业出版社,2010:548-553.

[2]李志辉,罗平等.统计分析教程[M].北京:电子工业出版社,2010:380-381.

[3]施朝健,张明铭.Logtistic回归模型分析[J].计算机辅助工程,2005,14(3):74-78.