一种生成残局数据库的倒推算法

梅 险，陈泳吉，何 哲，潘子翔，陈姝含，周 霖

(哈尔滨理工大学 a.计算机科学与技术学院;b.测控技术与通信工程学院，哈尔滨 150080)

爱恩斯坦棋[1]是一个以随机性为主要特征的博弈项目，对于所有参与者具有信息对称的特性。建立棋局数据库是一种能够静态保存棋局状态及对应棋局胜率的方法。对于爱恩斯坦棋的棋局数据库如何调用倒推逆向分析算法来有效“穷尽”棋局的状况，取其中部分局面生成残局库，是本文主要的研究方向。

在博弈对局中随着对局的进行，棋盘棋子数量逐渐减少的相关棋类最终不存在平局的情况，我们称这些棋种是收敛的。将爱恩斯坦棋作为这类棋种实现残局数据库的标志性代表。

“残局”是对双方棋子均已行动但双方仍然处于对峙状态的一种描述，我们可以在有限的内存中存储残局数据构建成为残局数据库。对于完全信息博弈项目在博弈双方完全理性的情况下，一个局面最终的胜负是确定的，残局数据库仅需存储每个局面使用搜索算法与逆向分析之后最终的胜负情况[2-3]，而对于爱恩斯坦棋的特性，必须存储一个局面的胜率，通过比较不同局面的胜率去选择最优走法[4]。

残局数据库的存在能够大大降低胜率评估时的计算复杂度。此外，由残局数据库得到的胜率是真实的胜率，其精确度远高于通过算法对胜率的估计，因此，可以将搜索算法同残局数据库进行有效结合，从而提高对局的最终胜率[5]。

在本文中，通过推导逆向分析代码，实现在各方棋子数量均不超过3的情况下的倒推计算，建立残局数据库。最终通过实验证明，倒推算法生成的残局数据库能够有效提高搜索算法效率[6-7]。

1 局面胜率的倒推公式

局面胜率分为“已走胜率”和“未走胜率”，对局双方均有此概念定义，以下概念描述以己方为例。

“己方已走胜率”指己方落子后形成局面的胜率。“己方已走胜率”对应的局面为己方达成胜利条件的局面。

“己方未走胜率”指对方刚走完，己方尚未行动时己方的胜率。“己方未走胜率”对应的局面为对方达成胜利条件的局面(为了理论上的对应，认为对方达成胜利条件的情况下，存在己方处于未走且己方胜率为0的状态)。同时，“己方未走胜率”所描述的局面是己方尚未掷骰子时的状态，已经掷骰子的状态另有概念。

为了区分玩家未走时骰子的情况，将掷骰子后的胜率称为“掷后胜率”。玩家对局时要在此状态下做出决策。“掷后胜率”的计算除了须知局面信息外，还须结合骰子的点数。

对于一方“掷前未走”的状态，另一方就是“已走”状态，2种状态相互对应，因此将“掷前未走”状态下的胜率称为“未走胜率”，而“掷后未走”是便于整体计算的一种中间状态。双方胜率的相关计算同理。状态的转换关系如图1所示。

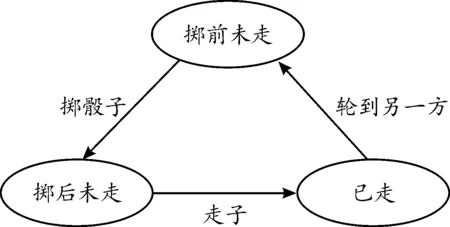
图1 状态的转换关系

爱恩斯坦棋属于零和博弈，且不存在平局的情况，因此在同一局面下双方胜率之和为1。对应一方的“已走”状态下就是另一方的“掷前未走”状态，那么已走状态下胜率为“已走胜率”，对应对方的“未走胜率”。即在某一局面B下，设已走状态为a，未走状态为b，己方为W，对方为W′，则己方已走胜率等于1减去对方未走胜率的差：

(1)

在本文中，等于骰子数的己方棋子存活时，该棋子称为上子，当棋子已不存在时，大于骰子数的最接近存活己方棋子称为上子；小于骰子数最接近且存在的己方棋子称为下子。对于每方可以走的棋子均有横走、竖走、斜走3种走法。

以u、d分别代表点数p对应的上子和下子，h、s、x分别代表横走、竖走、斜走(对于红方为向右、向下、向右下；对于蓝方为向左，向上，向左上)，那么对于集合B(1)(p)元素最多为B(1)(p)={Bpuh，Bpus，Bpux，Bpdh，Bpds，Bpdx}(如Bpuh代表在B局面下点数p的上子横走所形成的局面)，且其中一些元素可能由于无下子、走法越过棋盘边界等情况导致其不存在于场上。

掷后胜率：符号设为Wr，为当前局面B与骰子数p下每种可行走法后形成新局面的已走胜率Wa的最大值，即Wr(B，p)=maxWa(B(1)(p))；对方同理，Wr′(B，p)=maxWa′(B(1)(p))。

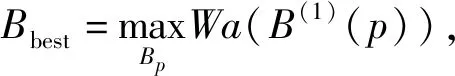
“掷前未走”状态下对应“未走胜率”，掷得每个骰子点数的概率相同，掷出骰子后转换“掷后未走”状态，“掷后胜率”对应“未走胜率”，那么未走胜率的数学期望就是当前局面点数1到6掷后胜率的平均值，设当前局面B下的未走胜率为Wb，则

(2)

式(2)建立了在某一局面B下“已走胜率Wa”“未走胜率Wb”“掷后胜率Wr”这三者中任意两者之间的互化关系，其中“已走胜率Wa”和“未走胜率Wb”两者的互化包含了敌我双方的胜率互化(图2)。

图2 各胜率的互化关系

对于3种胜率互化的式子联立可得：

(3)

式中，可视B为B(0)，即走0步后形成局面的单个元素的集合。B(0)若设定为己方为“未走”状态，对方为“已走”状态，则B(1)(p)为双方走了1步后对B(0)的双方状态进行交换后的状态，即B(1)(p)的状态变为己方为“已走”，对方变为“未走”的状态，以此类推，每步后的局面集合都对上一步的双方状态进行交换。

为了表述方便，将红方作为己方，蓝方作为对方。

在进行胜率推算时，可以保持以其中一方作为己方计算胜率，将双方“局面互换”。“局面互换”也包括“位置互换”和“颜色互换”。此时双方的“已走胜率”“未走胜率”“掷后胜率”也都交换，这时计算互换后红方的各胜率其实是计算蓝方的各胜率。将局面B进行局面互换后形成的新局面记作B′，则：

(4)

为了方便运算，用B′(i)(pi)来表示红方走了i步且每走一步都执行局面互换时所形成局面集合。当i为偶数，B′(i)(pi)=B(i)(pi)，当i为奇数，B′(i)(pi)等于B(i)(pi)每个元素都进行局面互换形成的集合。

在局面互换的条件下，根据式(3)，可得局面倒推的公式：

(5)

一方棋子对应的点数集合为p={1，2，3，4，5，6}，将B1(p)展开成集合，可以发现，对于一方连续的被移除棋子其对应点数集合PN={p1，p2,…,pn}，每个元素的上子相同，下子也相同。上子对应点数pu的可行走法为集合pN共有的上子可行走法{Bpuuh，Bpuus，Bpuux}，下子对应点数pd对应点数的可行走法为集合PN共有的下子可行走法{Bpuuh，Bpdus，Bpdux}，由此集合PN共有可行走法的集合为{Bpuuh，Bpuus，Bpuux，Bpduh，Bpdus，Bpdux}

可知对于集合PN中任意一个元素px都有B(1)(pu)∪B(1)(pd)=B(1)(px)，那么：

maxWb(B(1)(px))=maxWb(B(1)(pu)∪B(1)(pd))

(6)

因此不需要对被移除棋子的胜率进行单独计算，将之转化为棋上子或下子中最大未走胜率的倍率即可。于是设置未乘概率和倍率2个概念：当一个己方棋子存活时，其未乘概率等于对应的掷后胜率Wr(B，p)，否则等于0；初始每个棋子对应倍率为0，若该棋子存活则其倍率+1，否则其上子和下子中未乘概率最大的棋子对应的倍率+1，于是式子(2)可以化成以下伪代码：

2 倒推的架构

局面的数据以如下形式进行组织：以一个12位的26进制数代表一个局面，每一位分别代表双方每个棋子{1，2，3，4，5，6，-1，-2，-3，-4，-5，-6}的位置，数字0～24代表对应棋子在5*5棋盘上的位置，数字25代表对应棋子已从棋盘上移除(图3)。局面的情况对应一个特定的26进制数，该数可以作为胜率数组的下标。

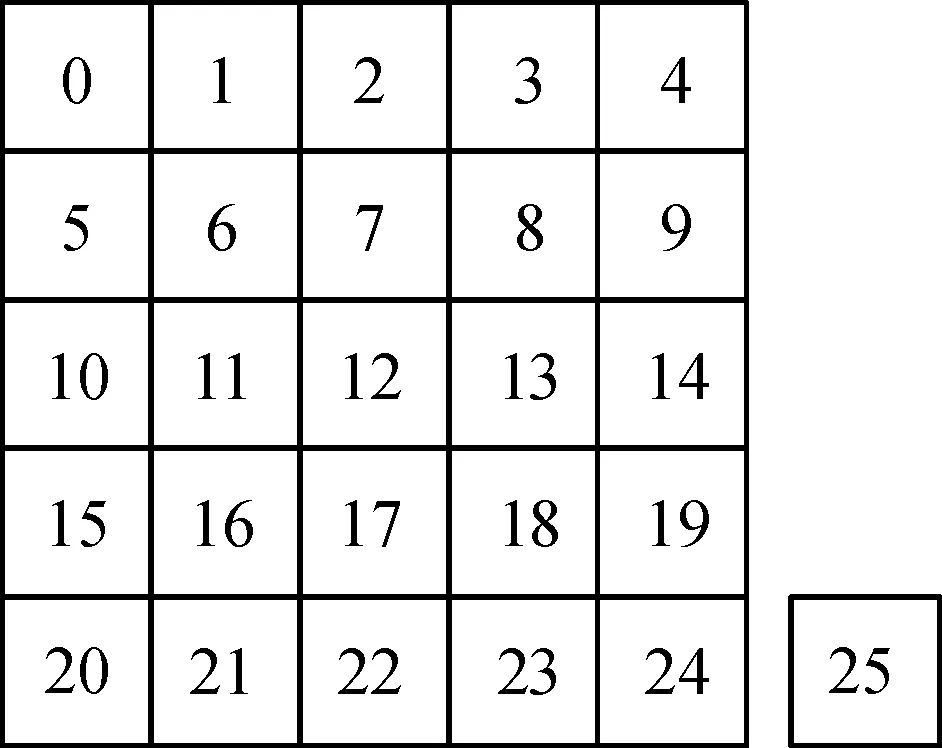
图3 棋盘位置编号示意图

“路径”指当前局面不断行棋直到游戏结束的具体走法。在一个路径所代表的走法中，双方移动的总步数就是该路径的步数。“路径经过该局面”指代路径行棋中形成的局面；“路径指向该局面”指代到游戏结束形成的局面。

“局面复杂度C”：指在某一局面下，所有路径的最大步数。路径上经过的每一个局面复杂度均比上一个局面对应的复杂度低。如图4所示。

图4 复杂度行棋推进示意图

3 倒推的过程

Wa({B′(1)(p)|1≤p≤6，p∈Z})均已生成是生成Wa(B)的充分条件，将以下函数称为对局面或局面集合B的正推展开，其中已胜局面是指达成胜利条件之一的局面：

(7)

即取B局面互换条件下所有路径中下一步所经过的全部局面的集合。经过正推展开得到的局面复杂度至少比原局面低1。当一个局面正推展开所得到的局面集合中所有局面已走胜率均已得知时，则可根据式(5)算出原局面的对应局面胜率。对于已知Wa({B′(1)(p)|1≤p≤6，p∈Z})，根据式(4)可计算Wa(B)，称局面B为{B′(1)(p)|1≤p≤6，p∈Z}的倒推收敛，为正推展开的逆过程：

g-1({B′(1)(p)|1≤p≤6，p∈Z})=B

(8)

对当前局面进行正推展开得到的末节点进行估值后，进行倒推收敛得到当前局面的估计胜率，这是爱恩斯坦棋使用极大极小值[8]算法构建博弈树的过程[9]。而对于UCT算法则是选择性的正推展开与倒推收敛[10]。

当对一个局面进行多次正推展开，直至完全展开到每一条路径的终点，最终会完全展开为一个已胜局面集合，而所有已胜局面对应局面胜率均为1，即已知。因此，任意存在的局面均可从已胜局面集合中倒推收敛，生成其对应胜率。

要生成Wa(B)，则需可倒推收敛于Wa(B)的局面先生成。这些所需局面相对于所收敛的局面来说，其对应的局面复杂度更低。将达成胜利条件的己方已走局面的局面复杂度定为0，先生成所有局面复杂度的局面，再依次生成C=1的局面、C=2的局面、C=3的局面，以此类推[11]。如图5所示。

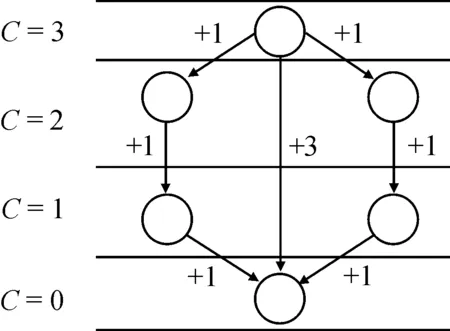
图5 倒推局面节点示意图

局面复杂度最高的局面为开局局面(任意排列的开局局面复杂度是相同的)。局面复杂度与棋子点数、摇到的随机数无关。在复杂度的视角里，局面只留下了己对方、位置2种属性。将已胜局面用复杂度0标记，把不存在局面用-1标记，未生成局面用-2标记。则局面复杂度标记集合为{-2，-1，0，1，…，i}，其中i为开局的局面复杂度。

将得到的所有正推展开包含局面B的局面集合，称为对B的倒推展开r(B)。这些局面包括了对于己方每个存活棋子在任意方向后退且不越过边界、不与其他棋子重叠所得到的局面，以及在每种情况都有在原位置重新放置任一已被吃的棋子，然后经过局面互换后得到的局面[12]。通过倒推展开局面B能够找出所有局面复杂度可能比B对应局面复杂度高1的局面。

r(B)={B1|B∈g(B1)}

(9)

在局面互换条件下的倒推过程中，将会以“临时局面复杂度c”对每个局面进行标记，以方便计算。总体局面为有存储、计算框架规定的所有存在局面与不存在局面的总和，在倒推前将总体局面标记为c=-2。在对某个局面的临时局面复杂度进行重新标记时，c=-1和c=0的局面不可被重新标记。图6为倒推时局面的生成流程。

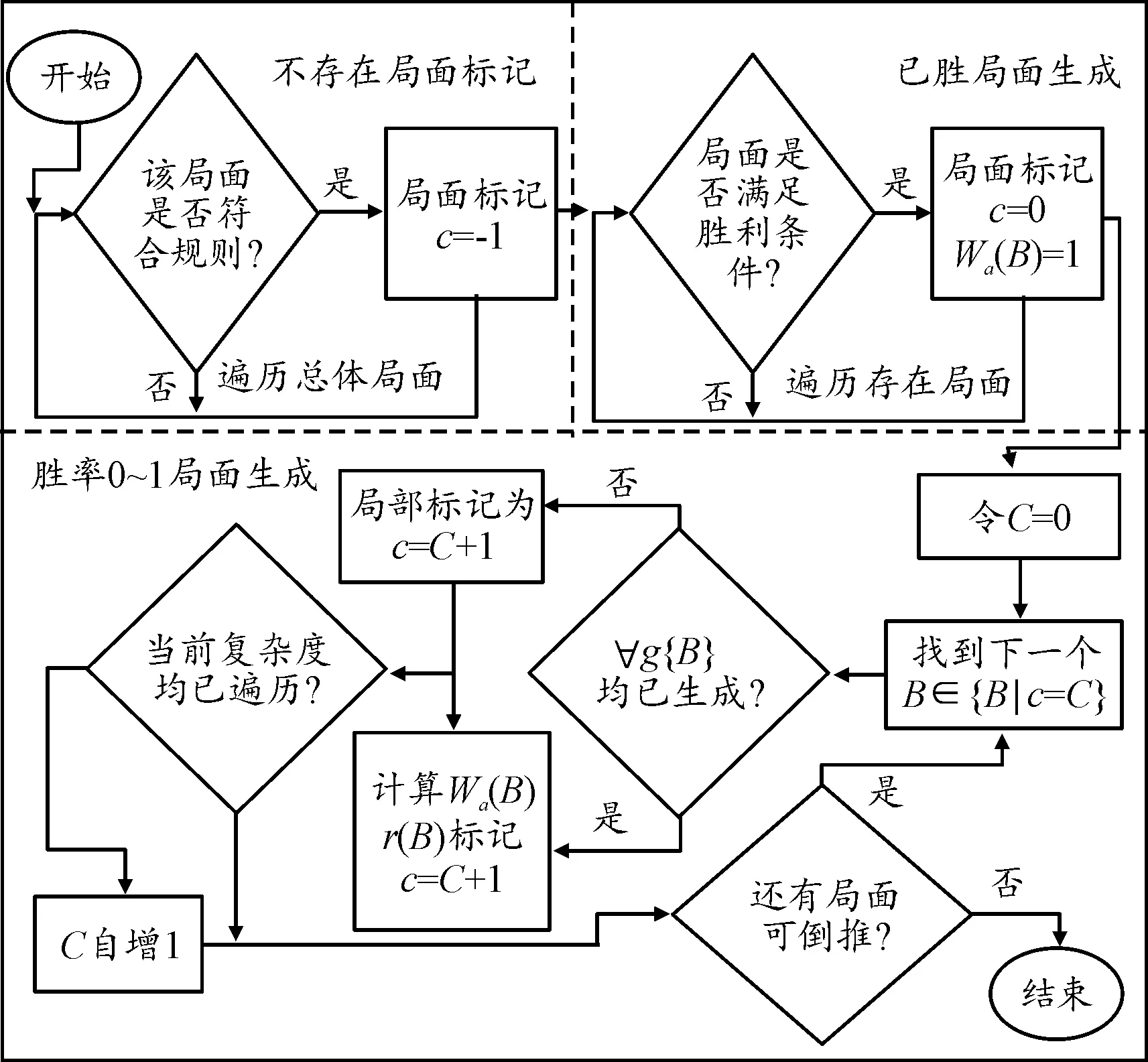
图6 倒推局面生成流程

这是一个由复杂度倒推生成局面复杂度的过程。当以上过程完成后，所有定义的局面都计算得到其准确胜率。

4 针对残局库的倒推

在当前生成如此庞大的数据量不现实，将只生成和存储部分已胜局面胜率数据作为残局库，利用存储的部分数据提高算法搜索效率与准确性，只生成和存储除指定的几个棋子外其他棋子都已被吃的局面的胜率。在进行倒推展开时，去除包含非局面组织棋子的局面，超出存储范围内的局面将不会被生成[13-14]。

爱恩斯坦棋残局数据库的局面数量仅与各方的棋子数有关，当残局数据库存储每方3个棋子时，局面复杂度分布如表1所示。

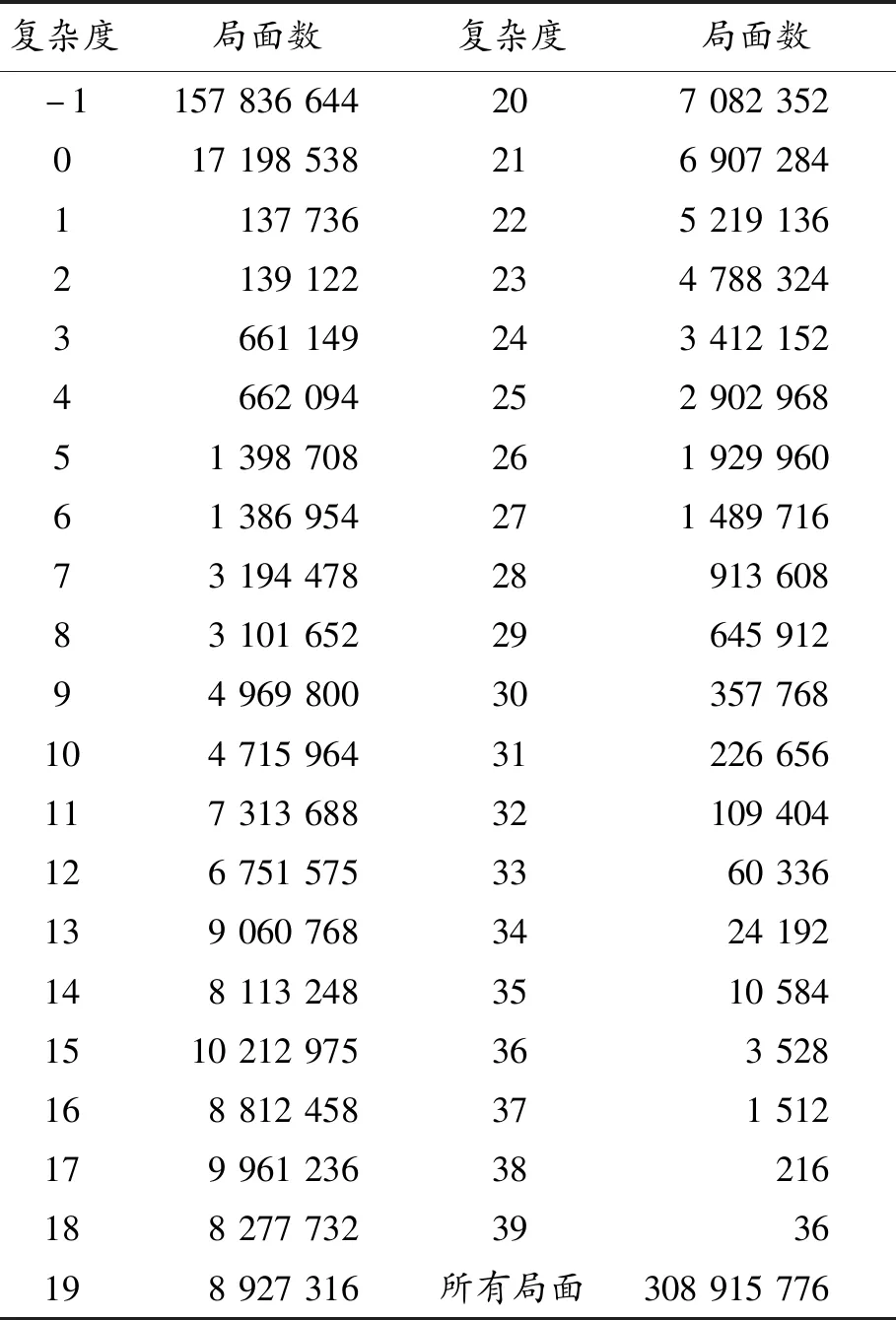
表1 局面复杂度分布

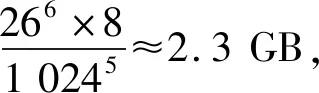
5 残局库的有效性验证

为了证实残局库的有效性与正确性，任意选取对局中的可穷举残局进行测试，从残局库中提取对应局面的已走胜率，与穷举搜索算法结果对比，验证残局库数据的准确性。例如在对局测试里，红1向3个方向移动后的形成局面的已走胜率如图7所示。

图7 局面胜率测试结果

在任意搜索算法可穷举局面中，残局库中保存的局面数据与穷举搜索算法得到的局面已走胜率数据完全相同，说明在可测试范围内。

将爱恩斯坦棋极大极小值α-β剪枝算法程序引入倒推算法获取残局库设为实验组，并将原程序设为对照组，比较实验组和对照组在对抗其他程序时的获胜概率。经过实验得到如图8所示的柱状图。

图8 引入残局库前后获胜概率

引入残局库后程序获胜概率显著增加，可知倒推算法生成的残局数据库能够帮助局面评估算法提升获胜概率。

6 结论

不仅是爱恩斯坦棋，对于任意收敛的信息对称博弈项目(包括随机棋类博弈)，都能倒推生成残局库，甚至在存储容量足够的情况下生成全部局面。但受到数据存储结构和容量的限制，爱恩斯坦棋倒推生成的残局库体量仍然不足。过去的研究中有使用逆向分析的方法获取完全博弈项目局面情况的，但由于其博弈项目不具有随机性，得到的局面情况若以胜率表示则非0即1，且推知胜率不需要计算。首次在随机博弈项目中详细研究了倒推生成局面胜率的方法，设计了按照局面复杂度逐步推知局面胜率的计算过程。通过该研究发现，生成的爱恩斯坦棋残局库可帮助其他搜索算法减少搜索量、提高准确性，以此提升算法的胜率。