基于EMD-LSTM模型的股指收盘价预测

刘 铭，单玉莹

(长春工业大学 数学与统计学院，长春 130012)

随着经济水平的提高，人民的物质生活极大丰富，越来越多的人选择投资股票进行理财。由于股票价格走势复杂，没有明确的规律，因此如何预测股指的走势成为投资者的一大难题，能够更好地预测股指的走势非常重要。

鉴于股价指数的波动性，如何透过复杂的现象了解股市的走势和资产价格的变动，从而使投资者获得理想的投资收益，是股票投资者特别是机构投资者非常关心的一个重要课题，也是一个需要深入研究的课题。要想选择合适的买入卖出期货的时机来产生超额收益，就必须选择一个合适的模型来有效地预测股价走势或预测未来价值。股市受很多经济和社会因素的影响，是一个复杂的非线性系统。传统的股票投资模型一般假设预测序列是线性或近似线性的，难以高效、准确地预测股指的价格走势，难以提供足够的信息支持股票预测优化投资决策。众所周知，深度学习算法能够从大量的原始时间序列数据中提取特征，无需依赖先验知识，非常适合金融时间序列预测，尤其是LSTM网络由于其循环性结构，具有长期记忆性。但股市是一个随着外部环境变化而变化的环境，随机性强，不同现象之间存在复杂的内在非线性关系，而目前的时间序列预测模型依靠单一的方法直接识别序列，不能充分提取复杂的序列变化信息，所以组合预测方法被提出。

通过现有文献发现国内外学者们较为关注股指金融问题[1-4]，传统预测金融数据的模型有例如ARMA模型、ARIMA模型和GARCH模型[5-10]，随着机器学习的兴起，研究者们发现对于时序数据的预测LSTM模型具有较好的效果[11-14]，后来对于单模型的不足，学者们发现可以在机器学习模型中加入优化算法使预测效果变好[15-18]。贺毅岳等[19]对沪深300的5个具有代表性股指用CEEMDAN与LSTM模型进行组合预测，结果表明模型具有较低的误差和滞后性。闫洪举[20]对于上证指数运用CNN与GRU模型进行组合预测，结果表明模型预测结果高于深度学习、机器学习算法。于家斌等[21]用GF优化算法搭建GF-LSTM网络的蓝藻水华预测模型，预测了水华发生。崔昊杨等[22]利用对遗忘门加权的方式改进LSTM模型，运用ARIMA模型和改进的LSTM对2018年国内某市区历史负荷电力数据进行预测，在数据缺失情况下的预测准确率分别提高了44%和57%。而经验模态分解(EMD)与机器学习模型相结合具有较好的预测效果[23-26]：Bao等[27]主要贡献在于首次尝试引入SAEs方法提取金融时间序列的深度不变日特征，构建WSAEs-LSTM、WLSTM、LSTM、RNN，其中WSAEs-LSTM具有最好的可预测性。Wang等[28]对纽约证券交易所、纽约证券交易所、富时指数和恒生指数构建了EMD-STNN模型，与STNN、BPNN和SVM摸型相比，EMD-STNN模型对训练集和测试集的预测具有明显的优势。

梳理已有文献发现：对于股指预测方面国内外学者已有一定研究成果，但鲜有提出股指波动对模型预测效果影响的文章。基于此本文提出了金融时序数据波动大小对于EMD-LSTM模型与LSTM模型预测效果的对应关系。数据波动越大，EMD-LSTM模型的预测效果越好。本文主要研究EMD-LSTM模型、EEMD-LSTM模型、LSTM模型和传统的时间序列模型在沪深300、上证指数和深证成指的收盘价预测中的应用并对其预测效果进行对比，然后在股指波动性不同的情形下分析EMD-LSTM模型和LSTM模型的适用情形。

1 研究方法

在构建EMD-LSTM模型对股指数据进行预测研究之前，需对模型组合的各组成部分：EMD分解技术及LSTM长短期记忆神经网络进行简要介绍。

1.1 LSTM深度神经网络

长短期记忆网络(long short term memory，LSTM)，最早由Hochreiter和Schmidhuber(1997)引入，发展到后期有许多学者进行了改进。LSTM的结构如图1。

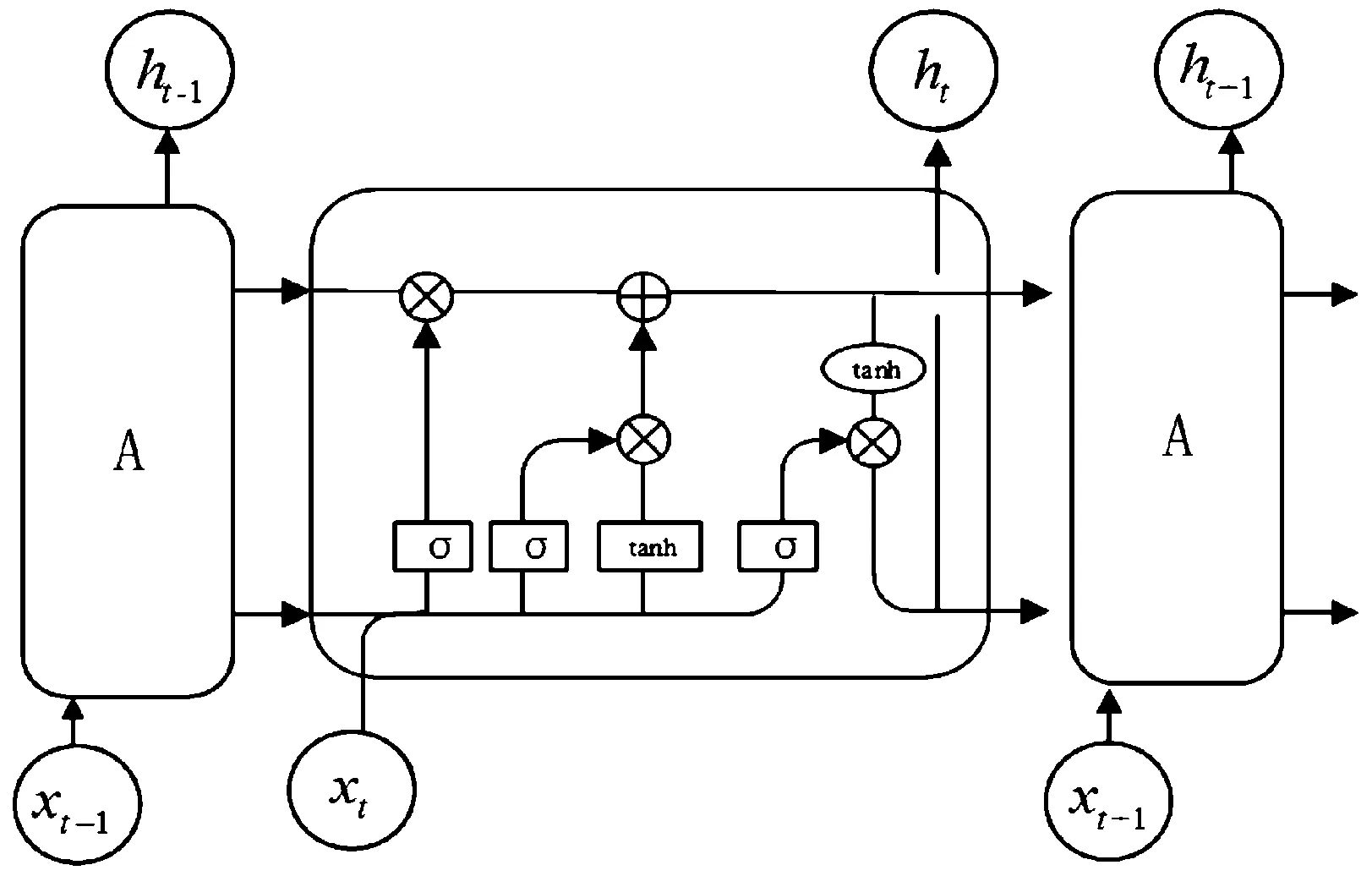
图1 LSTM结构示意图

LSTM具有链式结构，典型的LSTM网络由输入门、遗忘门和输出门构成。在t时刻时，输入数据xt以及之前时间步传递下来的更新，得到新的隐藏状态和记忆状态，并继续传递下去，利用这样的方式完成长期记忆。具体的数学描述如下：

输入数据xt和隐层输出ht-1经过“忘记门”，得到状态ft，表达式为：

ft=σ[Wf·(ht-1，xt)+bf]

(1)

其中：σ为sigmod函数，Wf为“忘记门”的权值向量，bf为“忘记门”的偏置值。

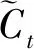
(2)

it=σ[Wi·(ht-1，xt)+bi]

(3)

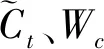
输入数据xt和隐藏状态ht-1经过输出门，计算出待输出结果ot，再经过t时刻的细胞状态Ct筛选ot中的信息作为最后输出ht，表达式为：

ot=σ[Wo·(ht-1，xt)+bo]

(4)

ht=ot*tanh(Ct)

(5)

ot、Wo和bo分别为输出向量、权值向量和偏置值。ht为t时刻LSTM模型的输出值。

1.2 经验模态分解

经验模态分解(empirical mode decomposition，EMD)，是由黄锷与其他学者提出的一种自适应信号时频处理方法。

对于任意的时间序列数据x(t)，EMD分解的计算流程如下：

步骤1 找出x(t)中所有局部极大值与极小值的大小和位置。

步骤2 极大值和极小值用上和下包络线进行拟合，并分别设U(t)和L(t)。

步骤3 计算上下两条包络线在每个时间点的均值：

m(t)=[U(t)+L(t)]/2

(6)

步骤4 令h1(t)=x(t)-m(t)，如果h1(t)满足IMF的判断条件，则得到了一条IMF。否则，令x(t)=h1(t)，将以上的步骤重复进行。

步骤5 上述步骤的运算可以逐步分解出第1，2，…，n个本特征模量即IMFi(t)，i=1，…，n，和一个残差r(t)。

此时，原始信号x(t)可以表示为：

(7)

同一个模量态函数包含多个周期特征。

2 实证分析

2.1 模型假设

在以上的讨论基础上，本文提出了基于EMD-LSTM算法的中国3个主要股指预测模型。该模型由2个部分组成，第一个部分是EMD算法，目的是将股指的日收盘价分解成IMF序列和残差序列。接着将IMF序列和残差序列分别构建LSTM模型，最后相加求和。EMD-LSTM模型结构如图2。

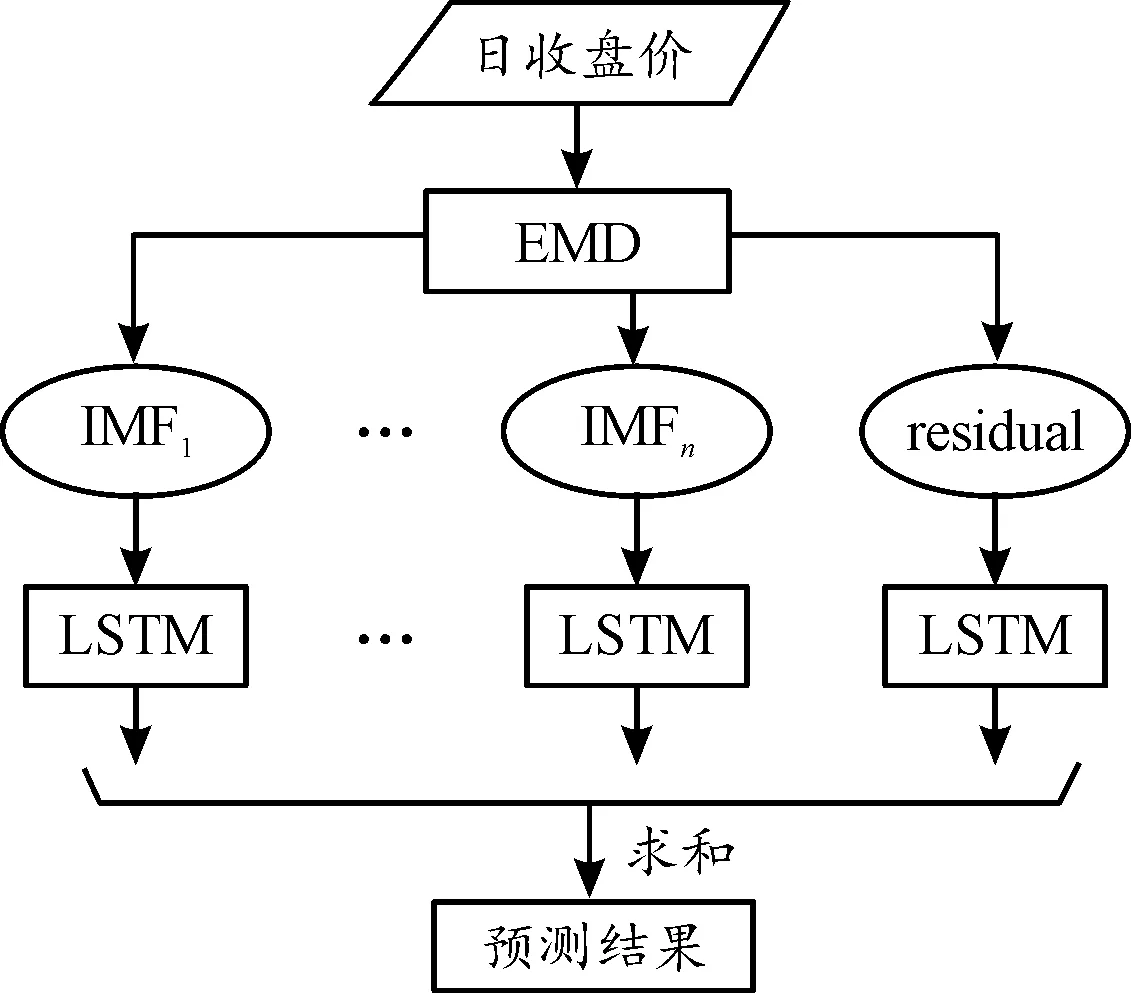
图2 EMD-LSTM模型结构框图

从图2可以看出，EMD-LSTM预测模型所采用的EMD分解算法可以满足金融数据的非线性、非平稳的特征。经过EMD分解后的数据输入LSTM模型训练。EMD算法和LSTM模型的优点在EMD-LSTM模型中体现。

本文神经网络模型采用滑动时间窗来构建样本，滑动窗口的宽度为50，预测未来一天的收盘价。通过不断后移，每次移动一个数据单位长度，形成一系列相互覆盖的样本数据，这样的方法在有效利用数据时序信息的同时降低了时变性。输入数据t与预测数据t+1的滑动窗口结构如图3。

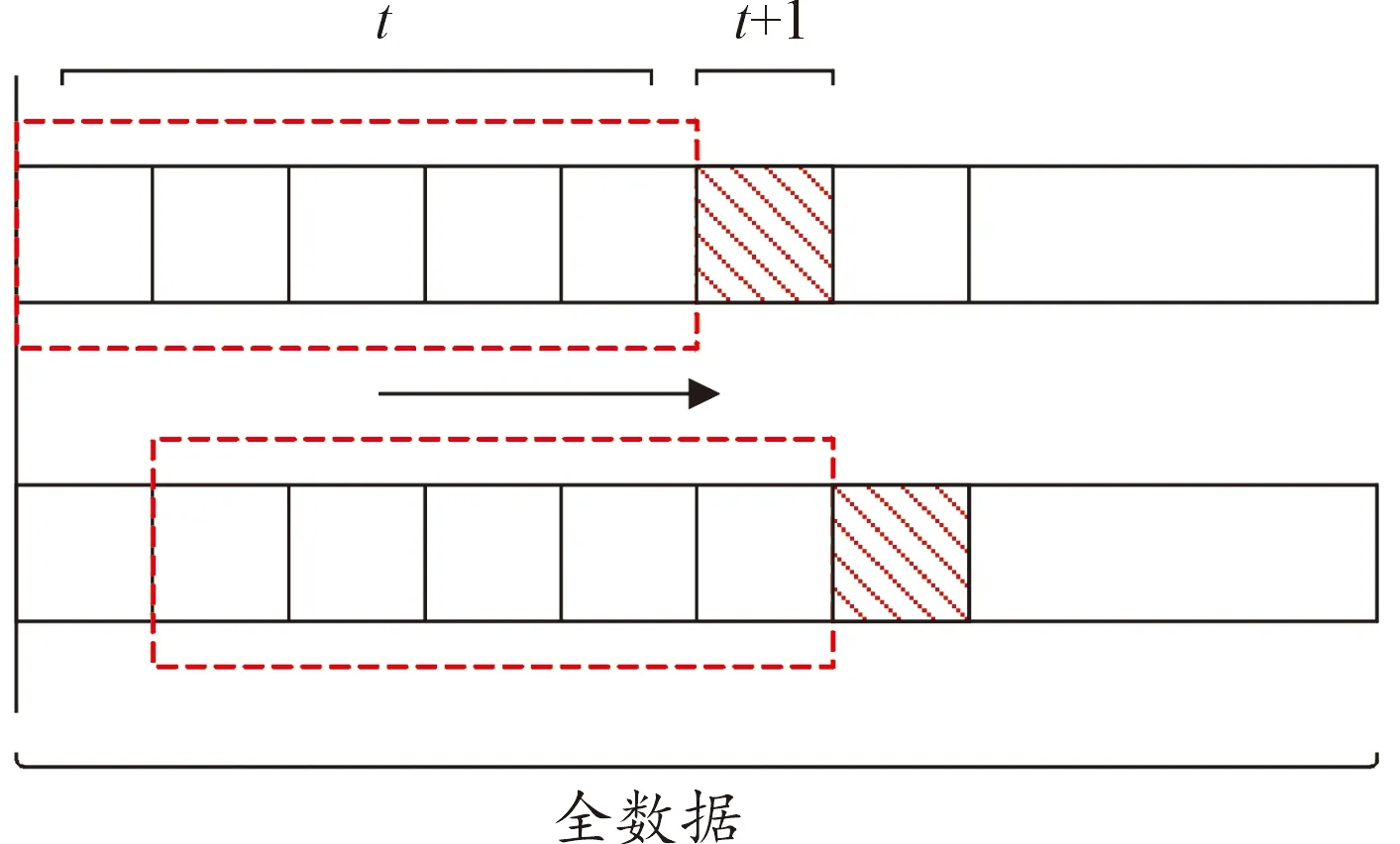
图3 滑动窗口结构示意图

2.2 数据获取与处理

2.2.1数据获取

本文主要研究对象为中国具有代表性的3支股票：沪深300股指期货、上证指数和深证成指2015年1月5日至2019年3月14日的日收盘价数据，共1 022个数据。来自Market Point。选取的中国3个股指收盘价数据如图4所示(其中横轴为时间，纵轴为股指收盘价价格)，收盘价数据的描述性统计如表1所示。

图4 股指收盘价数据

表1 3个股指收盘价的描述性统计

对3个股指的ADF检验得到的结果是序列不平稳，因此不能直接使用多元线性回归的方法。本文使用EMD算法可以去除收盘价数据的不平稳性，从而可以将不平稳数据分解为一些平稳时间序列和趋势项后，再将其作为输入。其中3个股指的方差相差较大，而方差是衡量数据波动性大小的指标，由表1可以看出上证指数的波动性远小于沪深300和深证成指的波动性。

2.2.2应用EMD算法对数据进行分解

从图5～7中可以看出：应用EMD算法将不同的股指，分别按其波动的数据类型划分为不同多个IMF序列和一个残差序列。

图5 沪深300EMD分解结果，IMF1-5序列和残差序列

2.2.3数据归一化

图6 上证指数EMD分解结果，IMF1-6序列和残差序列

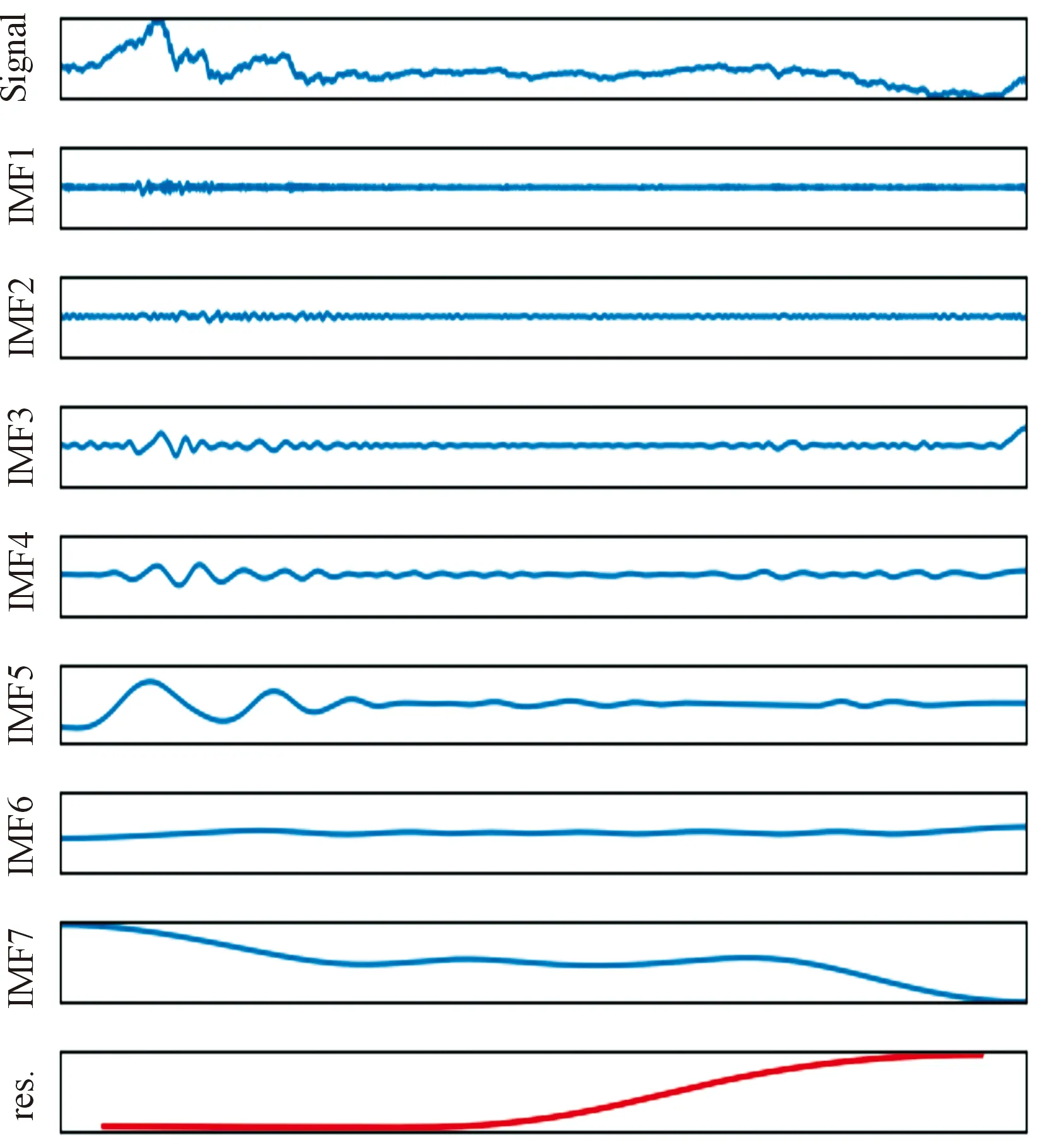
图7 深证成指EMD分解结果，IMF1-7序列和残差序列

在经EMD算法分解后的数据首先需要进行归一化处理，公式如下：

xnew=(xold-min(xi))/(max(xi)-min(xi))

(8)

式(8)中，xold为原始数据，xnew为归一化后的数据。

为了还原数据，还需要对预测的输出进行反归一化处理，公式为：

(9)

2.3 模型评价指标

本文选取的评价指标为均方根误差(RMSE)、平均绝对百分比误差(MAPE)、平均绝对误差(MAE)和确定系数(R2)。计算公式如下：

(10)

(11)

(12)

(13)

2.4 传统时序模型和EMD-LSTM模型对比实验

本章采用沪深300、上证指数和深证成指的收盘价数据，通过ARIMA、SVR、LSTM、EMD-LSTM、EMD-ARIMA、EMD-SVR和EEMD-LSTM这7种模型来测试股票收盘价的预测效果。

本文的预测方式是利用前50 d的数据预测第51 d的收盘价数据。训练的方式主要是取前67%作为训练集，后33%为测试集。

本文使用的软件为Python，本文的其他对比模型：在SVR模型中，选取的是sklearn库，核函数为rbf以及其他默认参数；在ARIMA模型中，选取的是statsmodels库，选取模型为ARIMA(1，1，1)；而LSTM模型中，选取的是keras库，LSTM的神经元个数为100，优化算法为adam，误差的计算方式使用均方误差，模型训练的epoch为650，batch size为100，Dropout为0.4；在EEMD-LSTM模型中，EEMD为集成经验模态分解，是将正态分布的白噪声加入原始数据后，再进行EMD分解，分解后的数据输入LSTM模型训练。

接着本文通过以上几种传统时序模型和EMD-LSTM模型对股指收盘价数据进行实证分析。

2.5 传统时序模型和EMD-LSTM模型收盘价预测结果

2.5.1沪深300股指基于各模型的预测结果

通过比较7种模型中的RMSE、MAPE、MAE和R2值可以看出：EMD-LSTM模型的RMSE、MAPE和MAE值最小，R2值最大，可以认为EMD-LSTM模型预测效果最好(表2)。预测结果如图8所示。

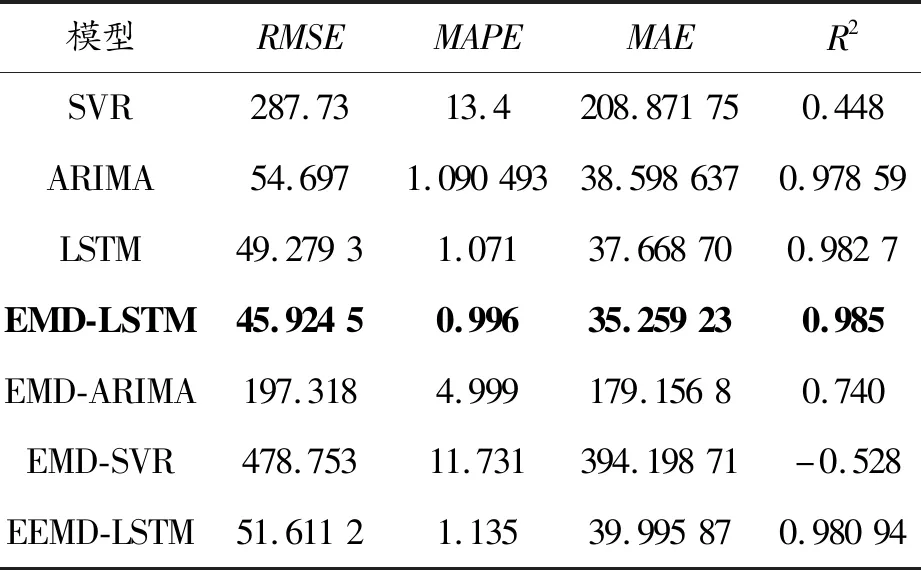
表2 沪深300基于各模型预测结果

图8 沪深300收盘价-EMD-LSTM模型预测曲线

数据波动的大小对于模型的预测效果有一定的影响，沪深300的方差相对较大，波动较大，EMD-LSTM的预测效果最好，这也能体现出EMD对非平稳波动大的数据预测效果良好。

2.5.2上证指数基于各模型的预测结果

通过比较7种模型的RMSE、MAPE、MAE和R2值可以看出，LSTM模型的RMSE、MAPE和MAE值最小，R2值最大，可以认为LSTM模型预测效果最好(见表3)。预测结果如图9所示。

图9 上证指数收盘价-LSTM模型预测曲线

基于上述，上证指数的方差相对较小，波动较小，LSTM的预测效果最好，这也能体现出LSTM对于非平稳波动小的数据预测效果良好(表3)。

表3 上证指数基于各模型预测结果

2.5.3深证成指基于各模型的预测结果

通过比较7种模型的RMSE、MAPE、MAE和R2值可以看出，EMD-LSTM模型的RMSE和MAE值最小，R2值最大，只有MAPE值比ARIMA模型稍大，以多数服从少数原则可以认为EMD-LSTM模型预测效果最好(见表4)。预测结果如图10所示。

图10 深证成指收盘价-EMD-LSTM模型预测曲线

基于上述，深证成指的方差相对较大，波动较大，EMD-LSTM的预测效果最好(表4)。

表4 深证成指基于各模型预测结果

3 结论

金融时间序列所具有的不平稳特性对其预测效果造成了极大的影响。为了缓解这种不利影响，本研究采用了EMD与LSTM相结合的模型。本文以历史50 d数据预测第51 d的数据，在沪深300股指和深证成指的预测中，数据波动较大，EMD-LSTM神经网络具有较好的效果；在上证指数的预测中，数据波动较小，LSTM模型具有较好的效果。可以看出数据波动的大小对于模型的预测效果有一定的影响，在非平稳序列中方差越大，波动越大，方差大的数据EMD-LSTM的预测效果最好，而方差相对较小的数据LSTM的预测效果最好，这也能体现出EMD对非平稳数据的处理的效果良好。该研究针对方差所体现的波动性，为未来深入研究找到确定的临界值去选择更合适的模型，从而进一步对国内外股指进行有效预测提供了思路。