多主体干预下的三分意见群体网络舆情传播模型研究

张 静，王筱莉，3，4，赵来军，刘 璐，王美华

(1.上海工程技术大学 管理学院，上海 201620；2.上海理工大学 管理学院,上海 200093；3.上海交通大学 安泰经济与管理学院，上海 200030；4.上海交通大学 中美物流研究院，上海 200030)

随着新媒体平台的不断涌现，舆情传播方式发生了巨大的转变，从口口相传转变为随机性裂变式的网络传播。网络舆情的传播对社会安全、秩序稳定、经济形势等产生重要影响，越来越多的人开始注重网络舆情传播问题。各领域专家从社会学、心理学、传播学、管理学等多学科研究范式对舆情传播进行了研究[1]。许多舆情平台也开始建立，如新浪微博推出针对企业和政府的新浪舆情通服务、人民网推出舆情频道等。网络舆情传播问题已成为当今研究的热点。

由于社交网络中信息传播的过程与传染性疾病在人群中的扩散过程相似，为了解决信息在网络中的传播和控制问题，众多学者将传染病模型应用到在线社交网络中[2]。1927年Kermack等[3]提出经典的SIR模型，将模型中的人划分为3类：S(易感染者)、I(传播者)、R(免疫者)。1964年Daley等[4]借鉴传染病模型思想提出DK模型，进一步，Maki等[5]提出对DK模型修正后的MK模型。随着复杂网络的发展，Zanette[6]首次将谣言模型应用在小世界网络中对传播过程进行分析。之后，不少学者开始在复杂网络中考虑人类社会属性对传播过程的影响，Nekovee等[7]将遗忘机制加入谣言传播模型，Jiao等[8]在谣言传播中考虑遗忘和记忆机制，并得出遗忘机制和记忆机制在一定条件下会终止谣言的传播，Wang等[9]、王筱莉等[10]和赵来军等[11]分别考虑信任机制、怀疑机制、传播率和移出率对谣言传播过程的影响，使模型更加符合实际情况。

随着互联网的发展，网络信息传播中不断出现新的主体，已有不少学者对主体干预下的舆情传播进行研究。在媒体干预方面，陈波等[12]首次将传统的传染病模型推广到泛在媒体环境中的开放系统，结合网络舆论场和外部舆论场建立SEIR舆情传播控制模型；朱恒民等[13]在考虑媒体数量、报道力度和可信度的基础上建立舆情话题传播模型；张立凡等[14]将媒体对网民的影响抽象为强化度和分歧度构建SIaIbR模型；狄岚等[15]将意见群体划分为支持者、中立者和反对者，构建SI3R模型分析媒体干预的作用。在政府干预方面，王治莹等[16]界定政府干预作用，针对政府的应急决策设定参数对舆情传播模型进行分析；张亚明等[17]将政府干预和媒体干预结合建立SHIaIbR模型；王佳敏等[18]提出政府对舆情事件的干预是在负面情感比例达到某一特定值时才会进行。在意见领袖方面，意见领袖的概念于20世纪40年代由Lazarsfeld等[19](拉扎斯菲尔德)基于“两级传播”理论提出；王佳敏等[18]提出融合网民个体情感、意见领袖和政府调节等因素的突发事件应急响应模型；马宁等[20]将舆论传播分为2个阶段，分析舆论领袖在舆情爆发阶段和平息阶段发挥的2个不同作用的干预。

以上研究虽然已经充分考虑了舆情在不同主体干预下的传播过程，但研究这些主体共同干预对舆情传播的影响尚少。张亚明等[17]的多主体干预研究仅考虑了媒体和政府的共同干预；王佳敏等[18]考虑了意见领袖和政府对网民情感的影响，并未考虑媒体的干预。网络舆情传播过程是极其复杂的，为了使传播模型更加切合实际，考虑媒体、政府和意见领袖的共同干预对舆情传播的影响是十分有必要的。因此，本文综合考虑媒体、政府、意见领袖共同干预对网络舆情传播的影响，将媒体对网民的干预影响抽象为强化度、分歧度和渗透率3类，将政府对网民的干预影响抽象为震慑度和免疫度两类，将意见领袖对网民的干预影响划分为政府干预前和政府干预后2种不同的干预效果，同时将舆情传播者划分为支持者、中立者和反对者，以此构建多主体干预下的三分意见群体网络舆情传播模型。

1 多主体干预下三分意见群体舆情传播模型构建

1.1 模型描述

本文中网络媒体是指除去官方背景的，在微博、博客和论坛等网络平台上发布信息的新闻媒体和自媒体。政府是指在各网络平台上进行官方认证并对网络舆情进行管控的社交账号。意见领袖是指舆情事件中在网络平台上进行发声引导，影响力(转发、点赞、评论、粉丝数)在前10名，不包含官方背景的相关领域名人、专家等。

当舆情开始传播时，首先是媒体在平台上散发消息传递给网民，引导其转化为犹豫者并进入舆情事件参与讨论，媒体增加网民对舆情传播的作用称为强化度，用ε表示。媒体在平台上发表不同观点引导网民进行传播，导致网民从一个观点转化为另一个观点的作用称为分歧度，用η表示。网民在平台上接触并传播舆情事件时受不同媒体观点的导向作用，媒体影响传播者观点之间相互转化的作用称为媒体渗透率，用γ表示。

舆情初始传播时人数较少，政府不会进行干预，当舆情支持者传播人数达到阈值时政府才会介入舆情事件进行干预，其干预表现为震慑作用和免疫作用。政府采取相关措施对舆情传播做出惩罚达到减少舆情传播的作用称为政府震慑度，σ1、σ3、σ4、σ5分别表示政府对未知者转化为犹豫者、犹豫者转化为支持者、中立者和反对者的震慑作用。政府对群体进行知识科普、事件描述等措施提高群体对舆情事件的认知，进而达到对舆情事件免疫的作用称为政府免疫度，σ2、σ6、σ7、σ8、σ9分别表示政府对未知者、犹豫者、支持者、中立者、反对者转化为免疫者的免疫作用。

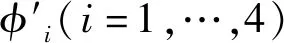
根据网络舆情传播特点，将群体划分为S(未知者)、H(犹豫者)、Ia(支持者)、Ib(中立者)、Ic(反对者)、R(免疫者)6类，构建多主体干预下的三分意见群体网络舆情传播模型(简称SHIaIbIcR模型)，具体如图1所示。其中，S(未知者)是指尚未接触到舆情的群体；H(犹豫者)是指未知者接触舆情事件后对舆情进行思考，并不直接发表观点进行传播的群体；Ia(支持者)、Ic(反对者)分别是指对舆情事件持支持、反对意见并进行传播的人群；Ib(中立者)是指由于舆情多发且反转较多造成一部分人对舆情的态度是中立的，并不直接进行支持或反驳的传播人群，目前此类人群在网络中是逐渐增多的；R(免疫者)是指已经传播过舆情或对舆情失去兴趣不再进行传播的人群。

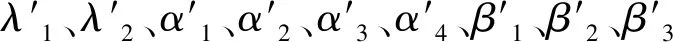
图1 SHIaIbIcR舆情传播模型示意图

图2 媒体干预下舆情传播模型示意图

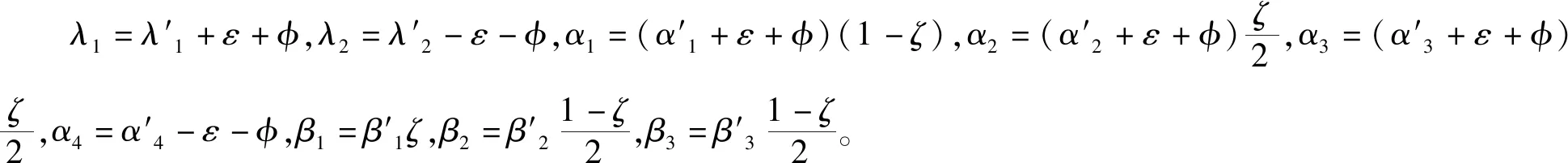
图3 媒体、意见领袖干预下舆情传播模型示意图

图4 媒体、政府、意见领袖干预下舆情传播模型示意图

1.2 动力学方程

舆情传播过程中6类群体在t时刻所占比例分别为S(t)、H(t)、Ia(t)、Ib(t)、Ic(t)、R(t)，网络社交平台作为一个开放性的平台，其用户数量随着时间不断变化，用常数A表示社交平台变化率，N表示社交网络平台中总人数，则A+S(t)+H(t)+Ia(t)+Ib(t)+Ic(t)+R(t)=N。根据图1不同群体相互转化关系，可知动力学方程为：

(1)

α3H-α4H

(2)

(γca-γac)IaIc

(3)

(γcb-γbc)IbIc

(4)

(γbc-γcb)IbIc

(5)

(6)

其中，S=S(t)、H=H(t)、Ia=Ia(t)、Ib=Ib(t)、Ic=Ic(t)、R=R(t)均为连续可微函数。

2 SHIaIbIcR舆情传播模型分析

2.1 平衡点求解

使用Matlab的solve符号演算可知式(1)～(6)微分方程不存在精确解，即无法得到该方程的精确平衡点。根据参考文献[14]，式(1)～(5)中不包含R(t)，通过简化方程组(1)～(5)得到方程组的4个平衡点：

(7)

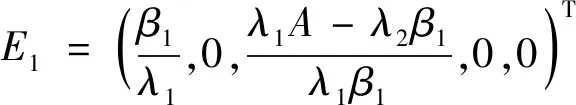
(8)

(9)

(10)

其中E0为无病平衡点，E1、E2、E3为地方病平衡点，通过计算可得E0点处的Jacobi矩阵如下：

(11)

(12)

2.2 基本再生数求解

在传染病动力学模型中基本再生数Ro是一个非常重要的参数，其代表在无干预情景下引入一个传染者在传染周期内可以传染的人数[21]。Ro的大小可以衡量舆情是否可以在网络平台上传播开，当Ro<1时网络舆情不会进行大规模传播；当Ro>1时网络舆情呈现大规模扩散趋势[22-23]。因此，本文基于传染病动力学理论利用下一代矩阵法求取式(1)～(6)的基本再生数。

令X=(H，Ia，Ib，S，R)T，根据文献[24]可构造出F(x)和V(x)，其中F(x)表示新增的网络舆情传播者，V(x)表示其他群体的密度变化，式(1)～(6)可表示为：dx=F(x)-V(x)，若将犹豫者转化为传播者而不看作新的感染，则

(13)

(14)

当系统中舆情不存在时，网络中仅有未知者，此时存在无疾病平衡点，E0=(0，0，0，S0，0)T则

(15)

(16)

不妨，令α1+α2+α3+α4=1，由A=FV-1可得

(17)

(18)

从R0表达式可知，基本再生数与网民移入率、未知者转化为犹豫者、免疫者及传播者转化为免疫者的比率有密切关系。当网民移入率和未知者转化为犹豫者比例增大会导致基本再生数增大，当基本再生数由小于1变为大于1时舆情传播规模逐渐变大，而增大未知者和传播者的免疫率会减少基本再生数。因此，对于舆情规模的管控可以集中在增加政府对未知者和传播者的免疫上(如增大λ2、β1、β2、β3)。

3 SHIaIbIcR舆情传播仿真模拟

舆情产生时，在媒体和意见领袖的导向作用下，网民对舆情的看法逐渐演变为3种不同的观点，不同观点之间相互影响并对舆情传播规则产生作用。政府干预系数正向或负向影响着舆情传播规律。政府干预后，意见领袖导向作用逐渐与政府干预方向一致，使网络舆情传播更快速地趋于稳定状态。为更好地说明网络媒体、意见领袖与政府多主体干预下的网络舆情传播规律，本节对不同主体干预情景进行了仿真模拟，分析不同主体干预时舆情传播变化。其中，初始值设置和仿真参数取值参考了张亚明等的文献[14,16]，通过控制变量等方法，对不同主体干预下的具体参数变化进行仿真模拟，并与无主体干预及主体干预基准进行比较分析，深入分析不同主体的干预系数对舆情传播的影响。

3.1 不同主体干预情景仿真模拟

本节使用Matlab R2020a软件进行仿真模拟，采用Runge-Kutta方法求解式(1)～(6)微分方程，对媒体、政府、意见领袖等主体不同干预的情景进行仿真模拟以验证理论分析。初始值设置为A=0.000 001，S(t)=0.5，H(t)=0.4，Ia(t)=0.04，Ib(t)=0.03，Ic(t)=0.03，R(t)=0。

图5 无主体干预下各群体密度变化曲线

图6 媒体干预下各群体密度变化曲线

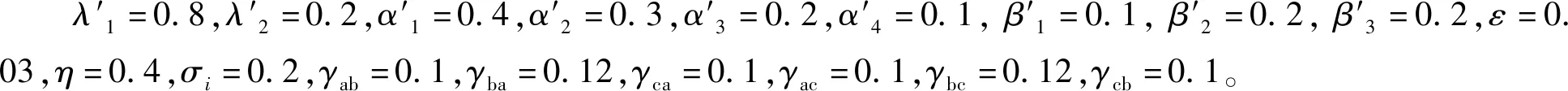
图7 媒体、政府干预下各群体密度变化曲线

图8 媒体、意见领袖干预下各群体密度变化曲线

图9 媒体、政府、意见领袖干预下各群体密度变化曲线

图5～9展示了5种情景下各群体的密度变化，其中图6为仅媒体干预下各群体密度变化。图7、8分别为媒体、政府与媒体、意见领袖共同干预下各群体密度变化。图9为媒体、政府、意见领袖干预下各群体密度变化。通过对比图5～9不同主体干预情况人群密度变化可知，图9所示的媒体、意见领袖和政府共同干预的舆情传播过程更加符合现实情况，舆情出现后首先是媒体和意见领袖对舆情进行散播和引导，舆情传播达到一定规模时政府进行干预，意见领袖受政府干预的影响改变自己的观点，进而在意见领袖和政府的作用下，舆情得到控制和弱化直至消失。

3.2 不同主体干预参数分析

3.2.1媒体干预下情景设置

1)强化度和分歧度对网络舆情传播的影响

为了探究媒体强化度和分歧度对各群体密度变化的影响，设置对照组和实验组进行模拟分析。图10(a)展示了2种强化度下各群体密度变化，其中实线表示强化度为0.02，虚线表示强化度为0.04，其他参数保持在无主体干预下的数值。图10(b)展示了2种分歧度下各群体密度变化，实线表示分歧度为0.4，虚线表示分歧度为0.6，其他参数保持在无主体干预下的数值。由图10可知，媒体强化度和分歧度均促进了传播者人数增长，且分歧度的影响大于强化度，所得结果与文献[13]和文献[17]一致。可知政府借助媒体进行舆情疏导时，需注意网民对媒体不同观点的接受度，若政府借助媒体宣传与主流观点相差较大的“官方观点”时，很有可能会增大网民之间的分歧讨论，使舆情在短时间内波及更大的范围。

图10 媒体强化度、分歧度对舆情传播的影响

2)渗透率对网络舆情传播的影响

图11(a)展示了中立者、反对者向支持者渗透时各群体密度变化，设置γba=0.6，γcb=0.3，γab=γbc=γac=γba=0.1，可知支持者人数明显增加。图11(b)展示了支持者、反对者向中立者渗透时各群体密度变化，设置γab=γcb=0.6，γba=γbc=γac=γca=0.1，可知中立者人数明显增加。图11(c)展示了支持者、中立者向反对者渗透时各群体密度变化，设置γac=0.3，γbc=0.6，γab=γcb=γca=γba=0.1，可知反对者的人数明显增加。由图11可知，渗透率促进了传播者观点之间的相互转化，增加了网民对舆情的话题讨论，舆情持续时间增长且不易消失，因此在控制网络舆情时，应减少传播观点之间的相互转化，疏导媒体在弱化话题讨论方向上保持一致。

图11 媒体渗透率对舆情传播的影响

3.2.2政府干预下情景设置

1)政府不同干预对舆情传播的影响

设置无主体干预和政府干预基准两个对照组，在政府干预基准上增加政府对不同群体的干预值，增加值为0.05，考察σ1、σ2、σ3、σ4、σ5、σ6、σ7、σ8、σ9的大小对各群体密度的变化影响。无干预对照组参数设置为：λ1=0.8，λ2=0.2，α1=0.4，α2=0.3，α3=0.2，α4=0.1，β1=0.1，β2=0.2，β3=0.2，政府干预基准参数设置为：λ1=0.7，λ2=0.3，α1=0.3，α2=0.2，α3=0.1，α4=0.4，β1=0.2，β2=0.3，β3=0.3。实验组参数设置为：λ1=0.65，λ2=0.35，α1=0.25，α2=0.15，α3=0.05，α4=0.45，β1=0.25，β2=0.35，β3=0.35。

图12(a)～(f)展示了政府不同干预下6种群体的密度变化。

图12 政府干预对舆情传播的影响

由图12(a)可知，与无干预情况相比，政府进行干预后仅有改变λ2的干预使未知者的人数有所减少，其他情景的干预效果均低于无干预情景下，且改变λ1的干预效果最差，说明政府若想减少未知者人数应重点采取措施干预未知者直接转化为免疫者。从图12(b)～(f)可知，政府不同干预下犹豫者、支持者、中立者和反对者人数相比未干预情况下都有所减少，免疫者人数有所增加。图12(b)中改变α4干预效果最好，而改变α1、α2、α3效果最差。图12(c)中改变α1干预效果最好，改变α2、α3效果最差，改变β1下降速度最快，因此政府在采取干预措施时，也可以重点考虑干预支持者转化为免疫者。图12(d)中改变α2干预效果最好，改变α1、α3效果最差，改变β2下降速度最快。图12(e)中改变α3干预效果最好，改变α1、α2效果最差，改变β3下降速度最快。图12(f)中改变λ2干预效果最好，改变λ1效果最差。网络舆情的治理体现在管控每类人群的数量，政府在控制舆情时首先要控制网络舆情的波及范围与所影响的人群数量[17]，即降低未知者、犹豫者和传播者人数数量，增加免疫者人群数量。对于不同人群的增加和减少，政府可以通过不同干预进行实现，如增加免疫者数量的最优措施是干预未知者转化为免疫者，减少犹豫者和传播者数量。

2)政府进行震慑干预和免疫干预的区别

政府只进行震慑作用下设置λ1=0.7，α1=0.3，α2=0.2，α3=0.1，政府只进行免疫作用情景下设置λ2=0.3，α4=0.4，β1=0.3，β2=0.3，β3=0.3，其他参数保持在无主体干预下的数值，将2种不同干预与无干预情景对比见图13(a)～(c)。由图13可知，对比无干预情况下，政府免疫作用起到了明显的干预效果，3种传播观点人数都得到了下降，但政府震慑作用对支持者和中立者的人数下降并未取得较好效果，说明政府对舆情事件进行管理时，应当重点将干预放在免疫作用上，以增加舆情信息的透明度，提高网民对舆情的认知，减少盲目跟风的传播行为。

图13 政府干预对传播者的影响

3.2.3意见领袖干预下情景设置

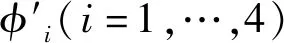
图14(a)～(f)展示了意见领袖不同干预下6种群体密度变化。在政府干预的影响下，意见领袖的干预使免疫者人数相比于未干预情况下有所增加，犹豫者、支持者、中立者、反对者有所减少。由图14(a)可知，对于未知者改变α1效果最差；由图14(b)可知，对于犹豫者改变α3效果最差；由图14(c)可知，对于支持者改变α1干预效果最好，而改变α2、α3效果最差；由图14(d)可知，对于中立者改变α2干预效果最好，改变α1、α3效果最差；由图14(e)可知，对于反对者改变α2干预效果最好，改变α1、α2效果最差；由图14(f)可知，对于免疫者改变α4干预效果最好，改变α3效果最差。综上所述，可知在政府干预的影响下，意见领袖对传播者的干预可以有效减少传播者人数，减少舆情波及范围，同时可以通过增加免疫者人数降低舆情传播规模，并重点干预使犹豫者转化为免疫者。

图14 意见领袖干预下不同群体密度变化曲线

3.2.4政府干预时间情景设置

t1、t2、t3、t4分别表示舆情支持者传播人数达到15%、20%、25%、30%的时间点，图15展示了政府在t1、t2、t3、t4时间点干预时各群体密度变化。由图15可知，政府干预的时间越早对降低舆情传播规模越有利。说明政府若可以较早觉察出舆情的爆发并进行干预，可以对舆情管控起到更好的效果，政府应当在考虑成本和收益之间做到舆情监测的最优化。

图15 政府不同干预时间下各群体密度变化曲线

4 案例分析

为了验证本文提出的SHIaIbIcR模型的有效性和意见领袖对舆情传播影响的理论分析，本文对新《中华人民共和国民典法》涉及的“侄子侄女可继承叔伯遗产”微博话题进行实证分析，利用“新浪舆情通”平台获取该舆情事件的数据。

该事件于2020年12月15日0点开始传播，共持续432 h，微博阅读量达3.2亿。而政府在舆情消亡期才进行干预(2020年12月21日)，舆情传播时受媒体和意见领袖干预较大，利用Matlab软件该事件进行模拟，得到该案例传播时传播人数的真实数据和模拟数据如图16所示。由图16可知，本文提出的SHIaIbIcR传播模型与实际传播模型趋势相符。图17展示了该事件中不同参与用户比例，网民比例最多，媒体次之，领袖和政府比例较少。图18展示了该舆情事件中网民意见比例，中性占绝大多数，与本文构建的加入意见领袖干预的三分意见群体模型相符合。且据“新浪舆情通”平台数据可知媒体粉丝平均值为1 877 500，平均带动转发为356，意见领袖粉丝平均值为27 963 470，平均带动转发为555，可知意见领袖的影响值大于媒体对网民的影响值，与本文构建的模型相符，验证了SHIaIbIcR模型的有效性。

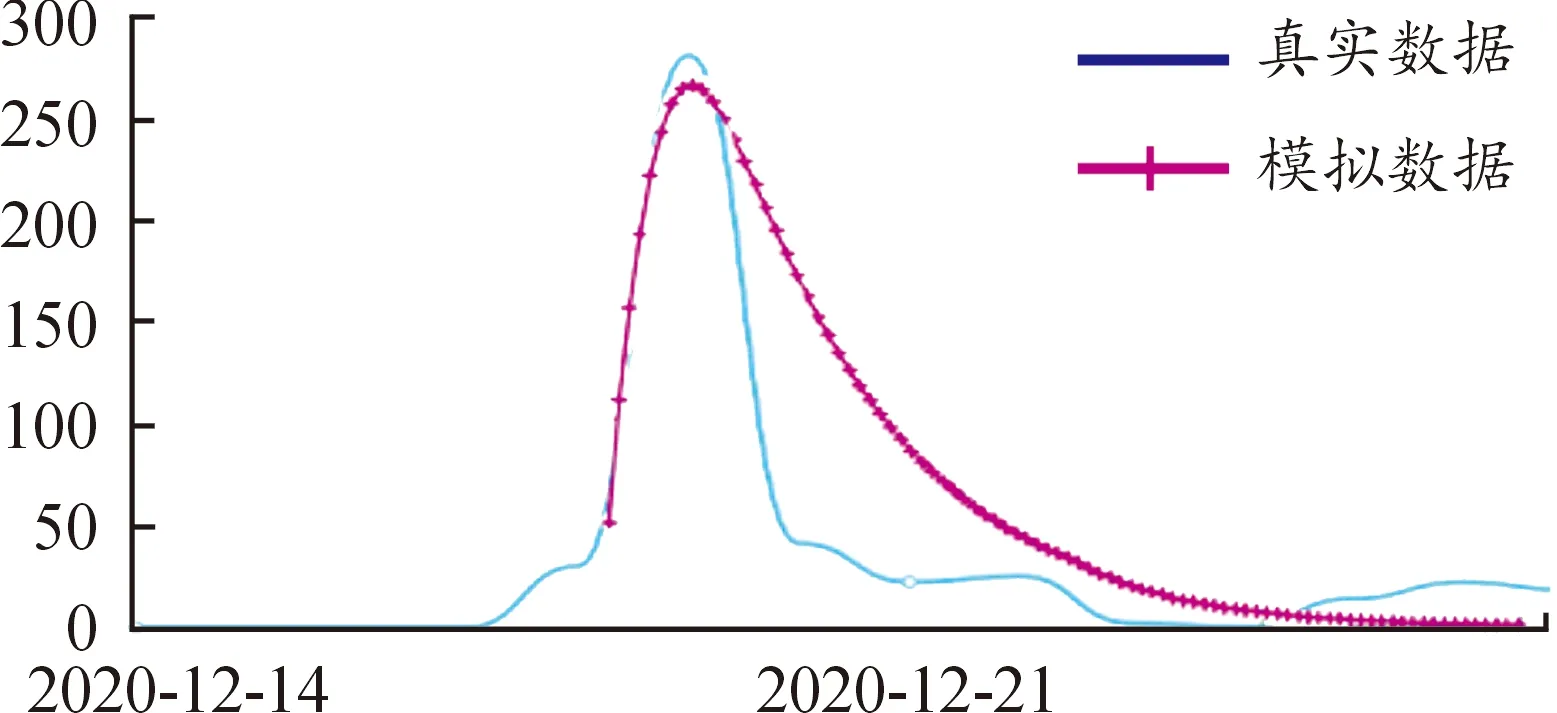
图16 “侄子侄女可继承叔伯遗产”舆情事件传播者密度变化曲线

图17 该舆情事件微博用户人群比例直方图

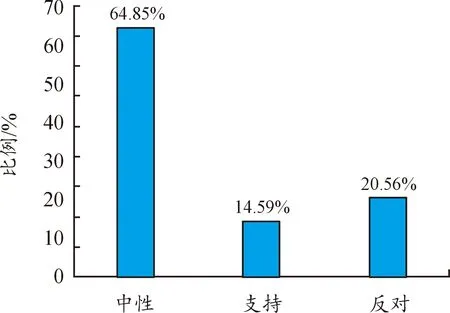
图18 该舆情事件微博用户意见比例直方图

在该舆情事件中，微博用户“021视频”为转发最多网民和评论最多网民，总转发人数达到 9 863条，总评论人数达到12 620条，其粉丝数为702 274，因此可认为微博用户“021视频”为该舆情事件的意见领袖，其观点对网民产生极大的影响。选取“021视频”用户为节点探究其对网民的影响，由图19、20可知，“021视频”用户作为“侄子侄女可继承叔伯遗产”首发用户，先直接影响“春涧生活派”、“北京全搜罗”等用户，这些用户影响较大其转发又会再次得到扩散。从图21可知，“北京全搜罗”用户在转发“021视频”用户内容后，其内容再次被“新闻晨报”、“娱乐女孩”等用户转发，观点得到3个层级的转发影响。可知在舆情事件中，意见领袖的影响是关键且不可忽视的主体，本文在多主体干预中加入意见领袖的影响使舆情传播模型更加符合实际情况。

图19 节点“021视频”微博转发云图

图20 节点“021视频”微博一级转发云图

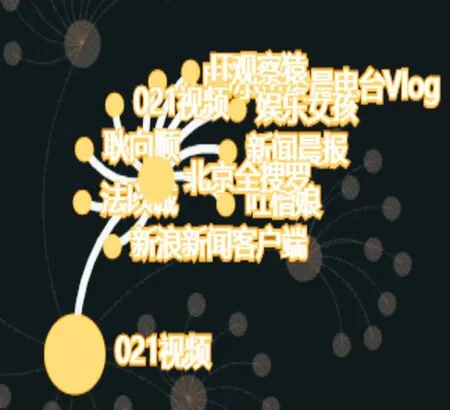
图21 节点“北京全搜罗”微博转发云图

5 结论

考虑到意见领袖对网络舆情传播的影响，提出媒体、政府和意见领袖共同干预下的三分意见群体网络舆情传播模型。依据舆情传播规则构建多主体干预下的SHIaIbIcR模型，给出各参数在多方主体影响下的定义和动力学方程，求出模型基本再生数；将媒体、政府、意见领袖的干预分别组合设置5种不同情景，利用Rung-Kutta方法对SHIaIbIcR模型进行数值模拟，并对相关参数的影响进行具体分析，利用真实案例验证了本文构建模型的有效性和合理性。结果表明：意见领袖在舆情传播中起重要作用，相比仅考虑政府和媒体干预下的舆情传播模型，考虑3个主体共同干预的舆情传播模型更加符合实际情况。但舆情事件的传播受到多方面的影响，如舆情当事人的回应对舆情发展趋势也有极大的影响，接下来会在该方面做进一步研究。