基于预期收益策略与UCT的德州扑克算法

王亚杰，丁傲冬，祁冰枝，张云博

（沈阳航空航天大学 a.工程训练中心；b.计算机学院，沈阳 110135）

机器博弈，也称计算机博弈，它既是人工智能领域的重要应用，也是研究人类思维和实现机器思维绝佳的实验载体，国内外很多学者一直进行不懈的研究［1-3］，各种国际、国内的比赛也促进了机器博弈理论和方法的快速发展［4］。机器博弈通常分为完备信息博弈与非完备信息博弈，如今完备信息博弈已经取得了重大突破，如谷歌的ALPHA GO［5］系列，通过使用深度强化学习算法在无需相关领域知识情况下实现多棋种对弈，达到了远超人类的水平。深度强化学习在电子游戏领域也取得了较好的效果，如Atari［6］。

由于对手信息的缺失，非完备信息博弈一直是机器博弈领域的难点，作为此类博弈的典型代表，德州扑克一直是人工智能领域内的难题［7］，分为有限注和无限注，玩家一般2～10人。本文以二人无限注德州扑克作为研究对象。

德州扑克常用算法有基于博弈树的搜索、虚拟遗憾最小化算法（counterfactual regret minimization，CFR）、对手建模等。2006年，Billings等提出了基于对手建模和树搜索的德州扑克算法［8］；2014年北京邮电大学的曹一鸣实现了基于上限置信区间算法（upper confidence bound apply to tree，UCT，一种基于蒙特卡罗的博弈树搜索）的德州扑克程序［9］，在结合了领域知识后取得了较好的效果。2007年，CFR被Zinkevich等提出［10］，同时证明CFR算法能够在二人零和博弈中达到近似纳什均衡，并且能够利用对手的弱点［11］；2015年，Billings等在CFR算法的基础上改进得到了CFR+算法，并证明改进后的CFR+算法能够解决二人限制性德州扑克，但是需要大量的相关领域知识［12］。2017年，来自加拿大Alberta大学、捷克Charles大学、布拉格捷克理工大学的研究人员们使用CFR算法结合深度学习实现的德州扑克人工智能系统DeepStack是世界上第一个在 “一对一无限注德州扑克”上击败了职业扑克玩家的计算机程序。2018年，浙江大学的李翔等提出基于手牌预测［7］（对手建模的一种）的算法，在结合领域知识的前提下首次在3人及以上无限注德州扑克上实现了对手手牌预测。

本文针对上述算法需要结合领域知识这一点，首先提出了预期收益策略，即每个阶段都根据每个可选动作的期望收益选择下一步动作。计算期望收益时考虑了3个指标：己方胜率、己方可选动作的下注量和损失率（下注量占己方总筹码量的比例）。己方胜率使用蒙特卡罗方法计算得到；己方可选动作的下注量代表动作执行完之后，己方在当前阶段的下注筹码总量；损失率代表己方如果输了要承担的损失。然后通过己方胜率和对手下注量评估对手胜率，得到对手胜率后把预期收益策略作为对手策略模型应用在UCT算法的模拟部分，即，将传统UCT算法用的随机模拟替换成双方都使用预期收益策略模拟。无论是计算预期收益考虑的3个指标还是评估对手胜率时用到的对手下注量都无需任何领域知识，因此改进后的UCT算法也是一种无需领域知识的算法。

1 预期收益策略

1.1 胜率的计算

在德州扑克中，游戏分为5个阶段：

Perflop（翻牌前）：每人发2张底牌，决定大小盲注，双方轮流表态（弃牌、跟注、下注）；

Flop（翻牌）：发3张公共牌，轮流表态；

Turn（转牌）：发第4张公共牌，轮流表态；

River（河牌）：发第5张公共牌，轮流表态；

比牌阶段：经过4轮的发牌和下注，双方选择最大5张牌，最大牌型的玩家赢得筹码。

上述5个阶段中前4个阶段都需要计算胜率作为表态依据，并且到一个新阶段胜率会发生变化。由于不知道对方底牌与未发的公共牌，所以采用蒙特卡罗方法进行计算。蒙特卡罗方法是通过重复随机采样来计算结果的一类概率算法。这里剩余公共牌满足均匀概率分布，对手底牌概率分布和对方策略相关，但是本文不考虑对手建模，仍然采用均匀概率分布。因此，随机地生成剩余公共牌与对方底牌，并统计双方胜负关系，将此过程重复，最终得到一个稳定的胜率作为当前阶段己方的胜率［13］。

本文采用蒙特卡罗方法计算胜率流程如图1所示。

图1 蒙特卡罗方法计算胜率流程

图2～5分别是在一次对局中Perflop、Flop、Turn和River 4个阶段模拟次数与胜率的关系，横坐标为模拟次数，纵坐标为己方胜率。

图2 Preflop阶段模拟次数与胜率关系

图3 Flop阶段模拟次数与胜率关系

图4 Turn阶段模拟次数与胜率关系

图5 River阶段模拟次数与胜率关系

在这4个阶段中，每次都随机地生成剩余公共牌与对方底牌，Perflop、Flop、Turn和River分别生成公共牌数量为：5张、2张、1张、1张；对方底牌数量为：2张。理论上，模拟次数足够多时得到的统计胜率就是真实胜率。从图像看，随着模拟次数N的增大，胜率W趋于稳定。表1统计了Preflop阶段N处于不同范围时的胜率情况。

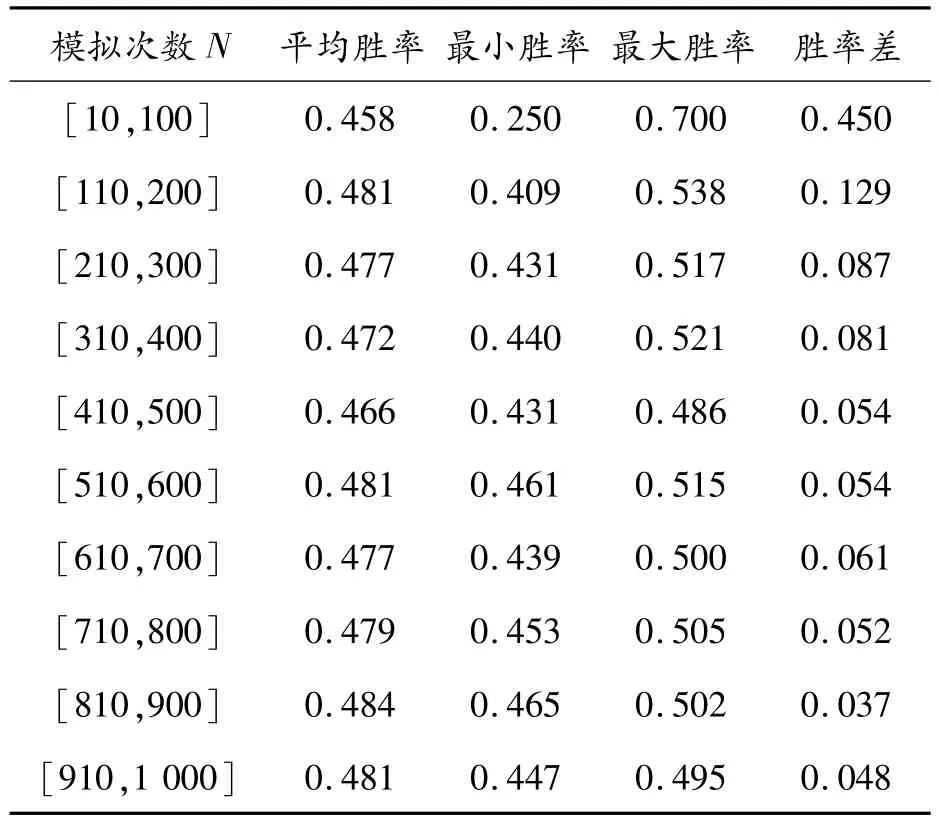
表1 模拟次数与胜率

表1的模拟次数N∈［a+10，a+100］表示N分别取值为a+10、a+20、…、a+100共10组值，得到10个胜率值，分别取最大胜率，最小胜率、平均胜率、最大与最小胜率差值。其中，平均胜率作为真实胜率的参考值，胜率差描述平均胜率的稳定性，值越小平均胜率越稳定。随着N逐渐增大，胜率差逐渐减小。当模拟次数N∈［810，1 000］时，胜率差小于0.05；当N∈［410，500］时，胜率差已经接近0.05，胜率已经非常稳定，可以代替真实胜率。同时，考虑到模拟次数越多耗时也会相应增长，实验中将模拟次数设置为500。

1.2 动作预期收益的计算

计算出当前阶段的胜率之后，根据胜率获得每个动作对应的预期收益。德州扑克中有5种动作：Fold、Call、Check、Raise、Bet、Allin。其中，Fold代表弃牌；Call代表将筹码加注到和对手一样多；Check代表不加注，看作将筹码加注到和当前一样多；Raise代表加注到指定筹码；Bet代表直接下注，可以看成直接把筹码加注到一个值；Allin代表剩余筹码全下注，可以看成直接把筹码加注到最大值，所以除了Fold之外的5种动作都可以用Raise代替，因此在程序中只有2种动作：Fold和Raise。Fold代表弃牌，执行Fold即损失所有下注筹码；对于动作Raise，需要根据胜率和对应下注量chip值计算出预期收益，用于估计动作的价值。用式（1）计算预期收益：

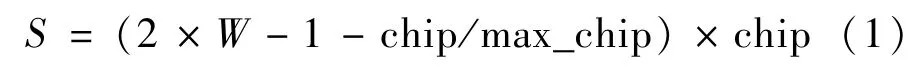
其中，S代表预期收益，W代表当前阶段己方胜率，chip代表当前动作的下注量，max_chip代表最大筹码量，即开局时己方拥有的筹码量。1-W是己方负率，W-（1-W）＝2×W-1是期望收益率。如果只考虑W则会出现期望收益率大于零时Allin总会被选为最佳策略；反之，Call或Check总会被选为最佳策略。考虑到无论选择哪种策略（除了Fold），都伴随着损失下注筹码的风险，因此引入损失率的概念，即下注筹码量占己方总筹码量的比例（chip／max_chip），比例越高，可能的损失越大。因此，在期望收益率的基础上减去损失率作为最终的预期收益率。在作出最终决策之前，先算出n个预期收益，加上选择Fold获得的收益，从n+1个收益中选择最大的收益对应的动作作为下一步动作。

图6是预期收益策略决策流程图。

图6 预期收益策略决策流程

基于预期收益策略的德州扑克程序THPZZ参加了2019届中国计算机博弈大赛2人非限制德州扑克项目，获得第3名。在实验中将作为基准程序与本文方法作对比。

2 UCT算法

2.1 传统UCT算法

UCT算法，即上限置信区间算法，是一种常见的博弈树搜索算法，该算法结合了蒙特卡罗树搜索和UCB（upper confidence bound）公式［14］，利用UCB公式进行选择。UCB公式来源于K臂强盗问题。K臂强盗问题是指一个具有K个手臂的强盗，每次用不同的手臂都可以获得具有不同分布的收益［15］。对于这个问题，首先把所有手臂尝试一次，然后根据式（2）：

蒙特卡洛树搜索有4个步骤：选择、扩展、模拟、回溯。UCT算法在选择阶段把蒙特卡罗树的每个节点看成K臂强盗问题中的强盗，把该节点的子节点作为强盗的K条手臂［15］，使用UCB公式选择下一个节点。

2.2 UCT与预期收益策略的结合

预期收益策略主要和蒙特卡洛树搜索4个步骤中的模拟结合，在蒙特卡罗树搜索中模拟是让博弈双方进行随机对弈［9］，直到终局状态。如UCT策略应用在围棋上时，当选择到一个叶子节点时，让双方随机下棋一直到结束，获得一个胜负结果，然后进行回溯更新节点信息。

这种模拟策略对于德州扑克来说虽然理论上可行，但是存在2个问题：

问题1：对于玩家来说每种动作被选择执行的概率不是均等的，牌型越好（即胜率高）的玩家平均下注量越大；反之，则越低。

问题2：模拟过程中缺少对手每个阶段的胜率信息，无法直接使用预期收益策略并且模拟到游戏结束时，不同于完全信息博弈，非完备信息博弈游戏不能得到一个精确的反馈值。例如：德州扑克中由于对方底牌不能确定，因此无法得到一个精确的胜负结果。

针对问题1，使用预期收益策略代替随机策略进行模拟。预期收益策略具有2个特点：①下注量与胜率正相关；②避免了随机策略里每种动作被选择概率都是均等的情况。在对对手风格、偏好完全不了解的情况下，预期收益策略完全可以作为一种对手平均策略模型来使用。

针对问题2，目前有2种解决方法：

①对手建模：利用对手下注信息估算出对手底牌范围，得到对手的胜率和最终的收益值；

②随机模拟：随机地给对方发底牌，得到对手的平均胜率和一个平均的收益值。

对手建模方法能够较为准确地预测特定对手的底牌［16-17］，但是比较复杂，本文主要研究了方法②，并对其做了一些改进。

对于方法②，虽然通过多次随机发牌能够计算出对方平均胜率并得到一个己方的平均收益值，但是用这种方法只能计算出对手的平均胜率，与实际情况略有差异。如果对手底牌较弱，实际胜率较低，多次随机发牌的方法相当于高估了对方的胜率，使得己方在做决策时平均下注量偏低，从而导致收益偏低。如果对手底牌较强，多次随机发牌的方法等同于低估了对方的胜率，容易误导己方加大下注量从而扩大损失。相比高估对方胜率情况，更需要避免低估对方胜率的情况，特别是在己方胜率低的情况下，低估对方胜率带来的损失更大。

基于以上分析本文提出了一种新的胜率模拟方法：通过多次随机发牌得到己方胜率Wself，把1-Wself作为对方胜率的一个基础值，同时考虑到把预期收益策略作为对手初始策略模型使用，因此把对手当前下注量chip与总筹码量chipsum的比值作为对方胜率的增量值。即使用式（3）计算对方胜率Wopponent：

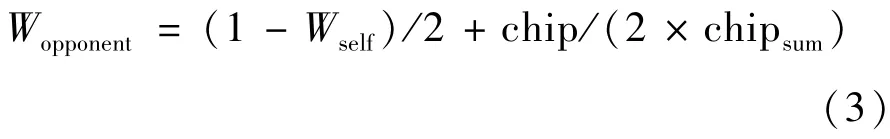
得到双方胜率估值之后，可用于预期收益策略并在结束时使用式（4）计算最终收益。

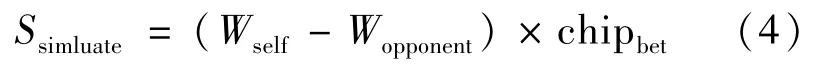
其中，Ssimluate是模拟到结束时的收益。chipbet是下注量。

对于式（3），考虑2种情况：

1）己方胜率较低。计算得到的对方胜率会一直处于较高水平。所以会出现状态1（己方胜率低，对方胜率低），此时会高估对方胜率。

2）己方胜率较高。计算得到的对方胜率取决于对方下注量的高低。所以会出现2种状态：状态2（对方胜率低，但下注量高）；状态3（对方胜率高，但下注量低）。这2种状态都会导致预测对方胜率不准确的问题。

相对于随机发牌的方法，式（3）在避免了己方胜率低的同时又低估对方胜率的情况。

在状态1中，己方会倾向于弃牌或下小注。

在状态2中，对方要想通过诈唬策略使己方弃牌，必须下注极高的筹码量，然而在对方Allin情况下，只有己方胜率低于2／3时会认为对方胜率高过己方，即当己方胜率高于2／3时，对方的诈唬策略作用不大。

在状态3中，双方有较大概率一直进行到游戏结束，通过比较牌型判断胜负，这种情况下由于己方胜率较高，在结果上没有明显劣势。综上所述，公式（3）使得在己方胜率较低（低于2／3）情况下倾向于较为保守的打法，表现为有最高总下注量限制；在胜率较高（高于2／3）情况下倾向于激进的打法，表现为无最高总下注量限制。

2.3 UCT与动作映射

对于无限注德州扑克，只要下注量在合法范围内都可以下注，如果下注量按照最小单位1来计算的话，下注行为会有很多种，构造出来的博弈树将会非常庞大。

动作映射［18］是把多个下注行为映射为一个行为，比如：将下注的筹码数规定为100的倍数，那么下注量在100周围（110、90等）的下注动作都可以用下注100代替。本次实验因算力有限，在确定最小下注量与最大下注量后，规定最小下注单位为500（仅在己方构建博弈树时限制），极大地减少了可选动作数量，从而降低了博弈树规模。

3 实验结果

3.1 实验环境与要求

本文的实验程序使用Python3.7实现，在一台AMD epyc 7k62（128核心），内存为512 GB，系统为windows server 2019的机器上运行。

德州扑克的规则按照中国计算机博弈大赛的比赛规则执行。即比赛开始时双方各有20 000筹码，每步策略计算时间不超过60 s。每进行完一局复位一次。双方进行100局比赛，累计每局赢得的筹码量，最后赢得筹码量多者获胜。

为了降低UCT算法构建的博弈树规模，在2.3节已经将模拟阶段的最小下注单位设置为500，起始筹码量为20 000，每种牌局状态的下一步动作最多为40个。在UCT算法中，选择、扩展、模拟、回溯是一次完整的搜索过程，搜索次数越多得到的结果越准确。模拟是一次搜索的子过程，在传统的UCT中一般采用随机的策略模拟1次得到结果并回溯。但在本文实验中，由于模拟过程中剩余公共牌与对方底牌（在采用随机模拟的UCT算法中存在）具有随机性，导致一次模拟得到的胜率随机性过大，所以需要进行多次模拟得到一个稳定的结果，进而需要设置2个参数：搜索次数与模拟次数。参数设置得越多，结果越准确，但是考虑到计算力有限，本文在对结果准确性影响不大的情况下尽量降低2个参数的值。

从表1结果分析得出：在计算胜率时，模拟次数N为［110，200］和［910，1 000］（这个区间的模拟次数最多，结果作为真实值参考）时得到的胜率均值差距较小，说明模拟次数超过100就可以得到和真实值接近的胜率。本文实验为了充分发挥硬件多核心的优势，将模拟次数设置为128（本文实验硬件的核心数量）次。当模拟次数设置为128次后，搜索次数直接决定程序运行时间，为了满足每步策略计算时间不超过60 s，将搜索次数设置为100次。

3.2 实验结果与分析

本次实验基准程序是THPZZ，分别和本文提出的2个算法进行对比：

算法1：UCT结合预期收益策略，采用随机模拟方式。

算法2：UCT结合预期收益策略，采用胜率模拟方式。

表2是采用胜率模拟与随机模拟的程序与THPZZ的比赛结果。

表2 实验结果

从表2中可以看出：算法2的水平高于THPZZ，THPZZ水平高于算法1。图7是算法2与算法1的比赛局数与累计赢得筹码的关系。

图7 比赛局数与赢得筹码量关系

从图7可以看出：算法2的策略较为平稳，随着比赛总局数增加，赢得的总筹码量稳定增长。算法1的策略随着比赛总局数的增长，赢得的总筹码量多次出现较大的起伏。

图8显示了在100局对弈中2个算法在不同下注范围的频数分布情况。

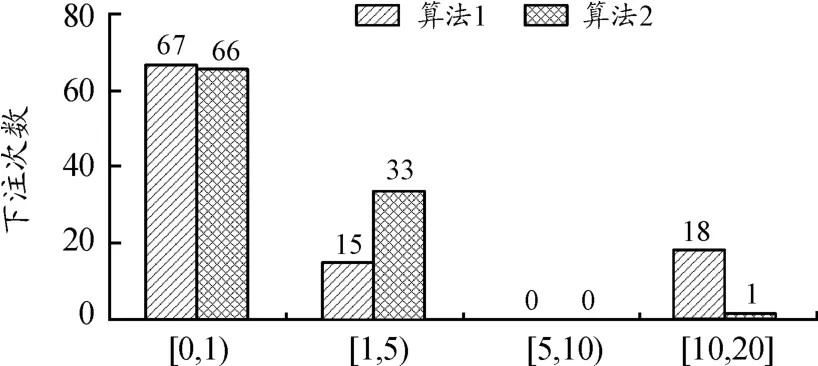
图8 下注范围频数分布

算法2在100次对局中有99次总下注量低于5 000，仅有1次下注量超过10 000的情况。总体策略较为保守。

算法1在100次对局中有82次总下注量低于5 000，18次总下注量超过10 000。

由于预期收益策略是根据己方胜率做出决策，而下注区间［10 000，20 000］对应较高的胜率。在与基于此策略的THPZZ的对比实验中，算法1由于在估算对手胜率时用的是随机模拟，因此得到的对手胜率是一个均值。由2.2的分析得知这种随机模拟在对手牌较强时得到的是比实际偏低的胜率，导致出现了多次盲目跟随对方下大注的行为。实际上在这18次下注量超过10 000的对局中，算法1仅有5次获得胜利。

而算法2采用式（3）估算对手胜率，由2.2的分析可知：这种估计方法在对手下注量较高的情况下估计到的对手胜率较高，能够改善随机模拟低估对手胜率的情况，因此下大注的情况较少，在100次对局中仅有1次。

4 结束语

本文提出了无需领域知识的预期收益策略，利用蒙特卡罗方法计算己方胜率，并根据己方胜率和对方下注量评估对方胜率，然后利用双方胜率与下注量计算不同动作的预期收益，最后根据预期收益选择下一步的动作，并且把预期收益策略与UCT算法结合，取得了较好的效果。

由于没有对手底牌的任何信息，预期收益策略在计算己方胜率时用的蒙特卡罗方法只能求出一个平均的胜率，在计算对手胜率时也只能根据己方胜率和对方下注量进行粗略的计算。因此，想要精确地获取己方和对方胜率，还需要结合对手建模的方法进行深入研究。