多目标铁路旅客乘车方案优化模型及算法研究

杨信丰,刘兰芬,李引珍,b,何瑞春

(兰州交通大学a.交通运输学院;b.西北交通经济研究中心,兰州730070)

多目标铁路旅客乘车方案优化模型及算法研究

杨信丰*a,刘兰芬a,李引珍a,b,何瑞春a

(兰州交通大学a.交通运输学院;b.西北交通经济研究中心,兰州730070)

铁路旅客乘车方案选择问题需要考虑不同旅客出行路径选择的影响因素.为了提高计算效率,首先对铁路客运网络进行适当简化,在分析影响旅客出行路径选择主要因素的基础上,以总乘车时间最小、总票价费用最少、换乘次数最少、换乘距离最短、换乘间隔时间损失最小及疲劳恢复时间最短为目标函数,考虑最大换乘次数的限制,建立铁路旅客乘车方案优化模型;并利用旅客列车时刻表设计旅客出行可行路径的快速搜索算法,根据可行路径集合,利用信息熵法确定各目标的权重,计算各可行路径的综合目标值,从而获得较满意的出行方案.最后,利用近期的铁路旅客列车时刻表,计算兰州至北京,兰州至长春的铁路旅客乘车方案.计算结果表明,可以得到旅客满意的出行方案.

铁路运输;乘车方案;多目标;换乘;信息熵

1 引 言

随着铁路六次大提速和客运专线的大量开通,旅客列车开行的数量和种类越来越多,这些硬件设施的加强使得越来越多的旅客选择铁路出行.这就要求铁路部门在加强硬件建设的同时提高服务能力,其中,针对旅客出行要求提供可选择的乘车方案就是一个值得研究的课题.

国内外关于旅客换乘的研究多集中在公共交通上,其中的方法和理论在铁路换乘研究中可以加以借鉴.文献[1]引入效用函数的概念,采用消费者依据效用最大化原则得到的出行路线更贴近出行者意愿.文献[2,3]分别运用直达矩阵、换乘矩阵和换乘有罚的方式建立了优化模型,设计了搜索换乘次数最少、所需时间最短的公交出行路径的算法.在铁路旅客换乘方面,文献[4]通过分析旅客乘车方案选择问题,对狭义最短乘车时间、最短换乘时间及最小乘车费用等8个目标进行分析,通过8个平衡系数综合以上目标,最终建立旅客乘车综合优化数学模型,根据旅客列车开行方案构造有向网络并设计了相应算法.文献[5]考虑旅客出行方案需求的差异性基于效用理论构建旅客换乘方案优化模型,并选用K短路算法求解.文献[6]通过增加虚拟点的方式构建基于列车运行时刻的换乘网络,并在此基础上,设计了有换乘次数限制的、总旅行时间最少的中转换乘模型,并采用遗传算法寻找最优解.文献[7]基于旅客列车运行时刻表,考虑换乘中转的影响因素根据旅客个性化需求设置相应的优先级,定义各类因素的加权和为“旅行广义时间函数”,构造出了一个动态规划数学模型及相应的A*算法.文献[8]设计了旅客对列车选择概率的多项Logit模型,并对影响因素选择及参数标定进行了研究.文献[9]以旅行目标值与换乘目标值之和最小作为目标函数,研究多目标权值的确定方法,提出最短路法和列车匹配法2种求解方法.

在实际应用中,由于出行者考虑问题的角度不同,对最佳乘车路线的理解就不同,问题不能简单地抽象为最短路问题.本文选择乘车时间、票价费用、换乘次数、换乘距离、换乘等候时间及舒适度等6个影响因素,建立多目标铁路旅客乘车方案优化模型,并根据路网结构、列车开行特点结合信息熵法设计求解算法.

2 换乘网络

我国铁路大小客运营业站有上千个,若构造一个包含全国铁路所有客运营业站的网络,计算量将非常庞大,从实际应用角度也没有必要.为提高效率,需要对路网进行适当的简化.本文以路网上对客运径路和换乘计算有影响的车站作为网络结点,删除无列车停站及只有一个列车停站的车站(始发站及终到站除外),将路网简化后保留下来的车站作为换乘网络的节点.

在简化的路网基础上以客运站作为网络节点,以两站间通过的列车作为有向弧,两站间列车运行时间作为弧的权,以列车的到发时刻作为节点的权值,构建乘车网络.设G=(V,L)为有向图.L={li|i=1,2,…,N}为列车集合,N为列车数量(上下行列车分别表示);i=1,2,…,N}为列车经过站点集合,其中Vli=为列车li经过的站点集合;Tli=为列车经过站点的时间集合,示li次列车到达s站的时刻,表示li次列车从s站的发车时刻;C={cli|表示li次列车的类型;设∈Vli,li∈L}表示列车的票价集合,为乘li次列车从i站到j站所用的票价;为换乘站点对集合,表示列车lk,lm可以在站点进行换乘,一般为同一车站或同一城市内的车站;为换乘站间的距离集合,表示lk,在站点的换乘距离.

3 换乘路径选择影响因素

旅客出行路径选择的主要影响因素包括乘车时间、票价费用、换乘次数、换乘距离、换乘等候时间及舒适度等.

3.1 乘车时间

铁路旅客乘车时间除了与所选线路、始发终到站里程有关外,还与所选列车种类(快、慢车)有关.用tij(li)表示乘li次列车从i站到j站所用的乘车时间

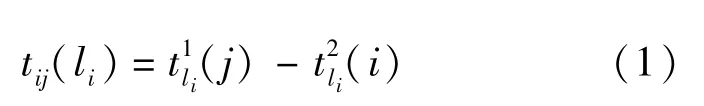
3.2 票价费用

铁路票价因列车等级、席座的不同而各异,列车的等级可分为:动车组、直特列车、特快列车、快速列车及普快列车等.我国铁路网中,任何铁路线路上的两站点间的铁路运价均可以在铁路列车时刻表上查询得到,在研究过程中,票价选用各种类的最低票价(如普通列车选用硬座票价)进行计算.那么乘li次列车从i站到j站所用的票价为pij(li).

3.3 换乘次数

换乘次数是指乘客在完成一次出行过程中所换列车的次数.由于换乘次数是乘客能直接感知的,因此换乘次数是直接影响乘客路径选择的一个重要因素.一般情况下,乘车时间差不多时换乘次数越少的路径被选择的概率越大[10].铁路中转换乘的旅客在途时间长、疲劳程度高,中转换乘耗时耗力,因此换乘方案中换乘次数一般是一个不大的值,设最大换乘次数为Nmax,为了方便计算旅客乘车方案,最大换乘次数值可取2.

3.4 换乘距离

由于换乘可能会在同一城市的不同车站进行,给换乘带来不便.换乘距离也是旅客出行路径选择的主要因素.如果换乘地点在同一个车站,则换乘距离较短,如果是不同车站,则换乘距离较长.为了便于计算,将在同一个车站换乘的距离设为0,即

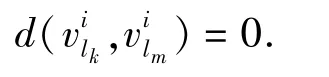
3.5 换乘间隔时间

换乘间隔时间为从l1次列车换乘l2次列车的时间,即l2次列车出发时刻与l1次列车到达时刻之间的时间差,若差值小于1个紧接续标准T0(一般取T0=20 min)[9],则时差应加一天,即1 440 min.那么乘坐l1次列车从i站到j站换乘l2次列车所需的换乘间隔时间tij(l1,l2)为

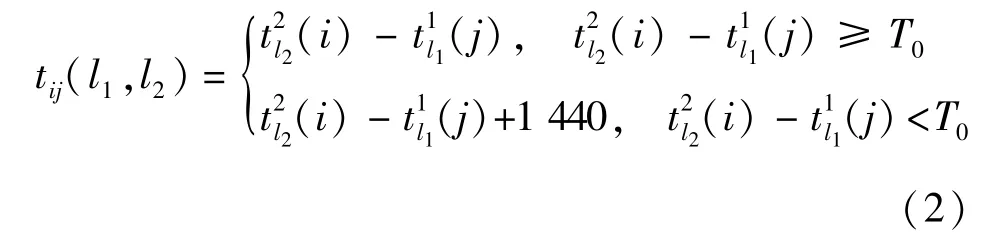
如果换乘间隔时间较长,则旅客需要等待较长时间进行换乘,特别是跨天的还需要吃饭、住宿,换乘成本较大;如果换乘间隔时间较短,则由于列车运行时间的随机性,可能会错过换乘列车,造成车票的浪费,一般乘客会选择换乘间隔在3～5 h之间的列车.本文设换乘间隔时间tij(l1,l2)的损失评价函数为

3.6 舒适性

舒适性是现代旅客交通运输追求的服务特性之一,本文采用文献[11]的研究成果,用旅行疲劳恢复时间来描述旅客选择不同车次出行的舒适程度.铁路旅客选择某车次出行的疲劳程度越大,需要的疲劳恢复时间越长,该车次的疲劳恢复时间的广义费用就越大[11].因此,本文选择乘坐某车次的疲劳恢复时间的价值来表示乘坐该车次的舒适度价值.铁路旅客乘li次列车从i站到j站的疲劳恢复时间[11]

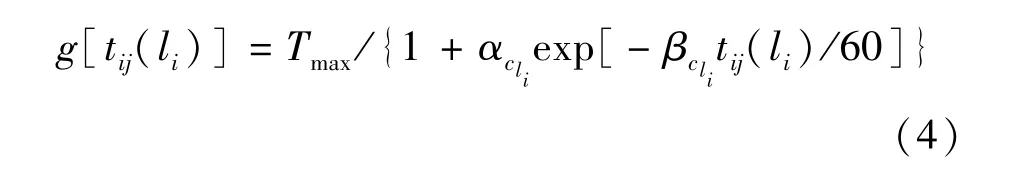
式中 Tmax表示恢复疲劳所需的最长时间参数,通常取14～15 h;αcli表示当乘车时间为0时,选择cli列车类型的疲劳恢复时间(即出行疲劳恢复时间的最小值);βcli表示单位出行时间的疲劳恢复时间强度系数,其值越大则疲劳恢复时间越长,参数βcli＞0.如果Tmax取15 h,则参数αc,βc的取值如表1所示[11].

表1 αc,βc取值Table 1 Values of αc,βc

4 换乘模型的构建

模型目标函数式(5)-式(10)分别为总乘车时间最小、总票价费用最少、换乘次数最少、换乘距离最短、换乘间隔时间损失最小及疲劳恢复时间最短.式(11)～式(13)保证从始发站o到终到站d为一条路径,式(14)表示换乘次数满足最大换乘次数Nmax的限制,式(15)是0-1变量约束.

显然,该换乘方案数学模型是一个多目标路径问题,属于多目标优化问题的一个子问题.

5 模型求解算法

多目标优化问题的目标函数通常彼此之间都是互相矛盾的,因此,采用传统最短路算法无法直接求得一条多目标最优路径.为了求解方便,可将模型求解过程分解为两个阶段:第一阶段进行可行路径集合的求解;第二阶段利用信息熵法确定各目标的权重,并对各条可行路径进行综合目标值计算,找出较优路径方案.

5.1 可行路径的搜索

由于旅客列车时刻表本身包含路径信息,因此,在进行可行路径集合的求解时,可以利用每个旅客列车时刻表的站点序列快速的得到多条可行的旅客出行路径.为了方便计算旅客乘车方案,取最大换乘次数Nmax=2.

对于一次出行需求od而言,首先在列车集合L={li|i=1,2,…,N}中,分别找出经过o站及d站的列车集合,并分别记为Lo,Ld.

直达方案求解思路:设Li=Lo∩Ld,则li∈Li列车均经过o站及d站,如果li次列车从o站的发车时刻早于到达d站的时刻,即,则表示从o站乘坐li次列车可以直接到达d站.

根据上述思路,铁路旅客出行乘车方案的具体算法步骤如下:

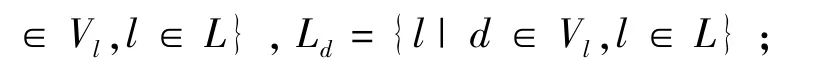
Step 2 如果Lo=Ø或者Ld=Ø,则停止计算,否则令Li∈Lo∩Ld;

Step 3 直达列车路径计算,如果Li=Ø,转至Step 4,否则,对于所有的若,则输出li列车从o到d站的路径,计算总乘车时间,票价费用换乘次数z3=0,换乘距离z4=0,换乘间隔时间效用z5=0及疲劳恢复时间,转至Step 4;

Step 4 一次换乘路径计算,令Lm=Lo-Ld,Lk=Ld-Lo,若Lm=Ø或者Lk=Ø,则停止计算,否则令且,如果,转至Step 5,否则,转至Step 6;

Step 5 输出lm列车从o到vlm的站点及Lk列车从vl到d的站点,构成一次换乘路径,计算总乘车时间,票价费用,换乘次数z3=1,换乘距离,换乘间隔时间效用z5=及疲劳恢复时间,转至Step 6;

Step 6 两次换乘路径计算,令Lq=L-Lo∪Ld,若Lq=Ø,则停止计算,否则,对于所有的lq∈ Lq,如果且转至Step7,否则,停止计算.

Step 7 输出lm列车从o到vlm的站点,lq列车从到的站点及Lk列车从vlk到d的站点,构成两次换乘路径,计算总乘车时间,票价费用,换乘次数z3=2,换乘距离,换乘间隔时间效用及疲劳恢复时间z6,停止计算.

5.2 可行路径的综合目标值计算

从o站到d站的可行路径集合的优选实质为多目标决策问题.信息熵法是一种常用的确定多目标权重的方法,该方法基于“差异驱动”原理,突出局部差异,由各个样本的实际数据求得最优权重,反映了指标信息熵值的效用价值,避免了人为的影响因素,因而给出的指标权重更具有客观性,从而具有较高的再现性和可信度;另外,信息熵法采用归一化方法对数据进行无量纲化处理,具有单调性、缩放无关性和总量恒定性等优异品质,且鲁棒性较好[12].

设可行路径条数为M,那么,M条可行路径及6个目标值就构成了一个决策矩阵,设这个决策矩阵为MAodM×6.那么利用熵值赋权法获得可行路径的综合目标值的计算过程如下:

Step 3 计算第j个目标的熵

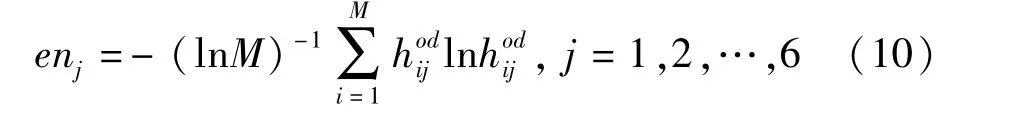
Step 4 计算第j个目标的权重系数

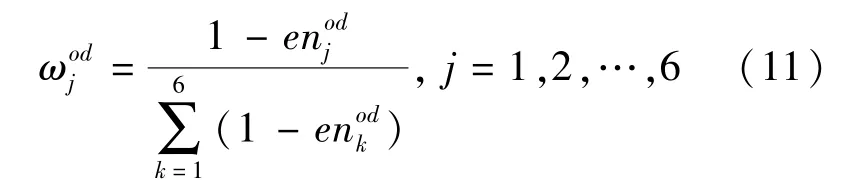
Step 5 计算路径i的综合目标值

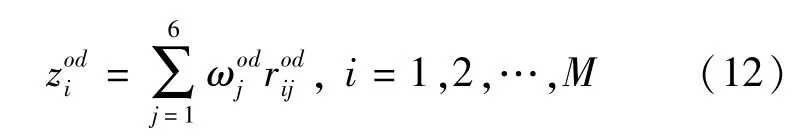
根据计算得到的综合目标值,按照从大到小对可行路径进行排序,排在前面的路径为较优路径.

6 算例分析

利用2012年7月份的铁路旅客列车时刻表,首先计算兰州至北京的铁路旅客乘车方案,选取最大换乘次数Nmax=1,经过计算得到可行路径2 438条,其中直达路径为6条,一次换乘方案中换乘城市为124个.利用熵值信息计算得到6个目标的权重为:0.001 8,0.004 9,0.509 8,0.005 3,0.471 8, 0.006 4.计算各可行路径的综合目标值,排在前15的路径的综合目标值及乘车方案如表2所示.从表2中可以看出直达方案的综合目标值远远高于换乘方案,说明该方法能体现换乘次数是直接影响乘客路径选择的一个重要因素的现象.对比方案的各目标值,发现目标z3及z5的数值差异较大,对乘车方案选择的影响较大,两个目标对应的权重分别为0.509 8及0.471 8,相对较大,这反映了信息熵法基于“差异驱动”原理的特点.

仍然选取最大换乘次数Nmax=1,计算兰州至长春的铁路旅客乘车方案,得到可行路径591条,全部为一次换乘方案,可换乘城市为66个.利用熵值信息计算得到6个目标的权重为:0.073 6, 0.0682,0,0.232 6,0.362 3,0.263 4.由于所得可行方案均为一次换乘方案,因此各方案的目标三的值均为1,该目标对方案的选择没有作用,从熵值信息计算得到的目标权重来看,目标三的权重为0,这也反映出信息熵法的客观性.计算各可行路径的综合目标值,排在前5位及后5位路径的综合目标值及乘车方案如表3所示.

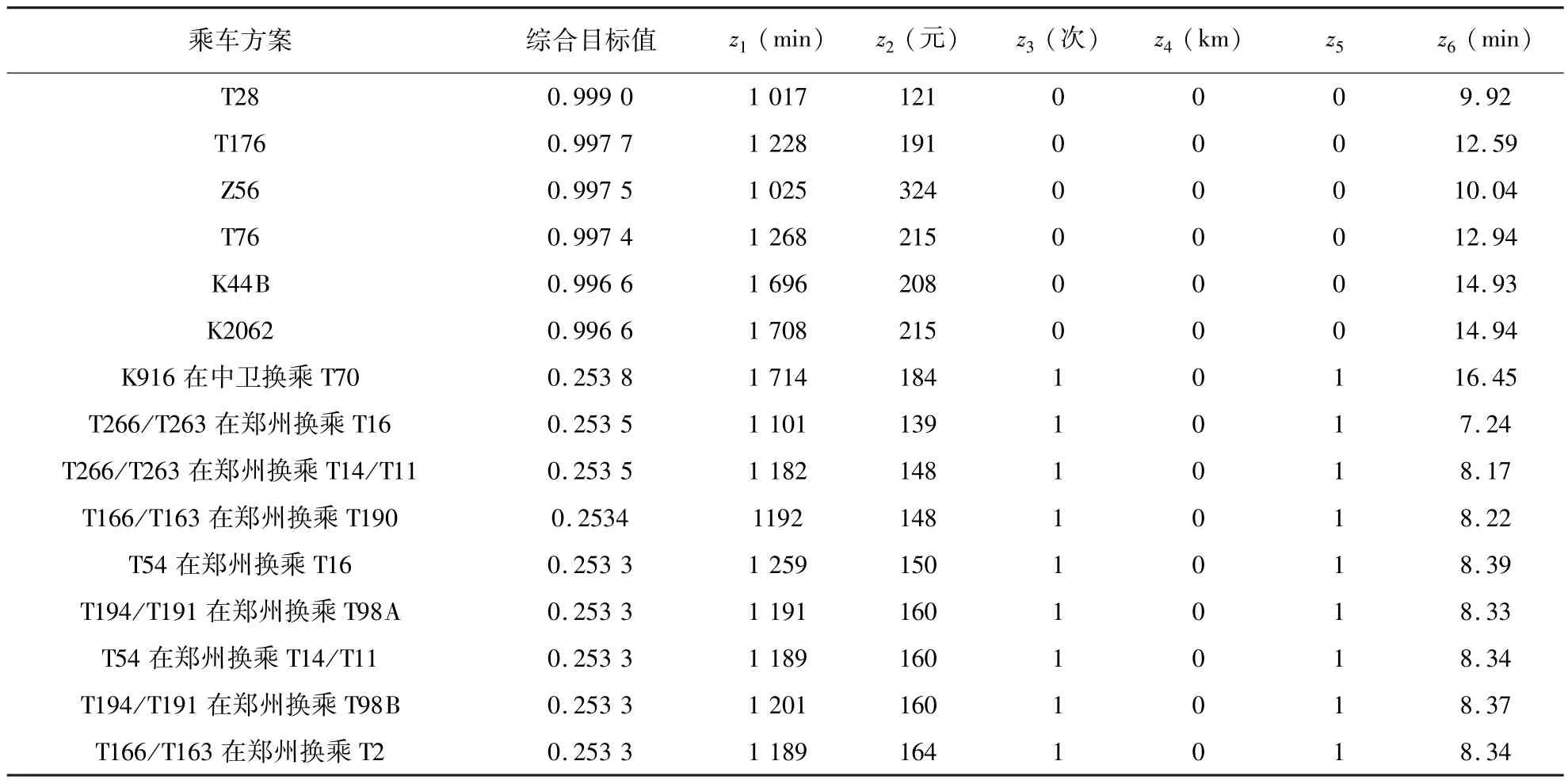
表2 兰州至北京的较优乘车方案及目标值Table 2 The optimal traveling schemes and objective values of Lanzhou-Beijing

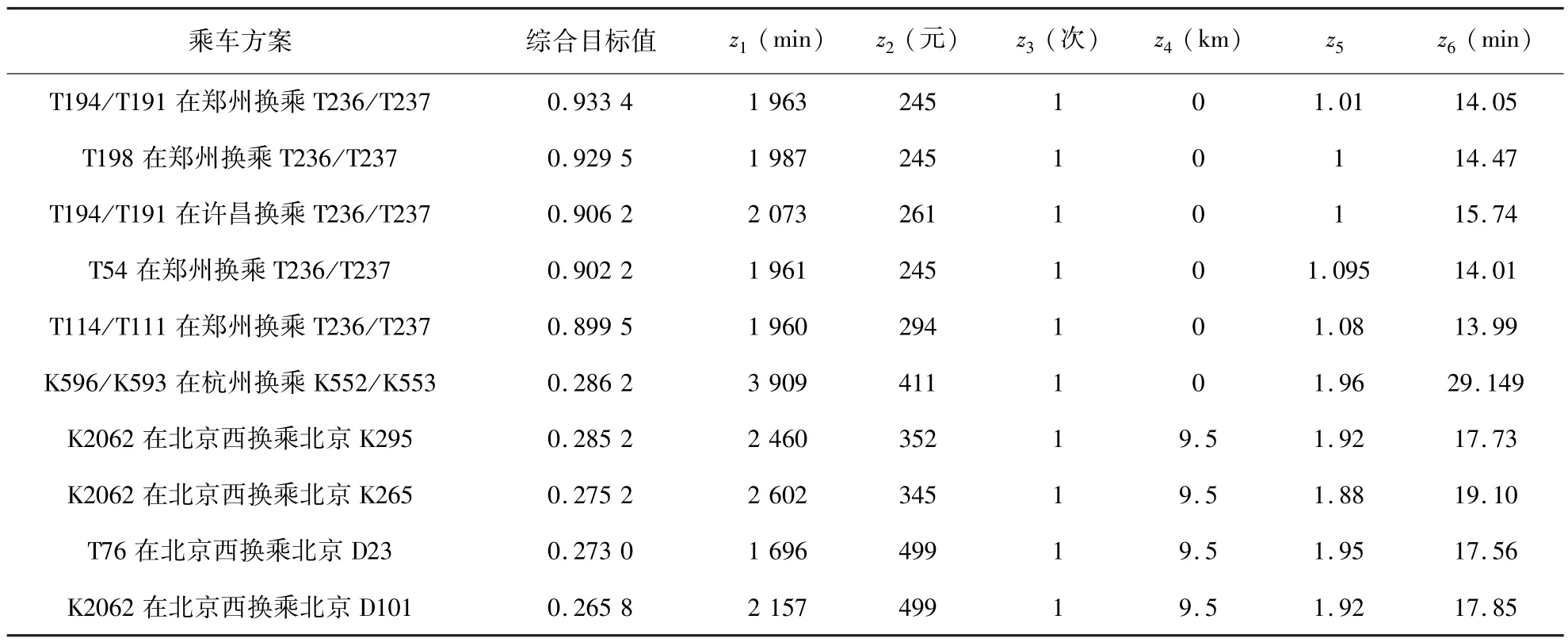
表3 兰州至长春的部分乘车方案及目标值Table 3 Some traveling schemes and objective values of Lan-zhuo-Changchun

表3中前5个方案为较优方案,后5个方案为较劣方案,对比前5个方案与后5个方案的各目标值,z4,z5及z6三个目标的数值差异较大,对乘车方案选择的影响较大,三个目标对应的权重也较大;另外,前5个方案均为同站换乘,而后4个方案为非同站换乘,对乘车方案的选择也有较大影响.

7 研究结论

由于出行者考虑问题的角度不同,对最佳乘车路线的理解就不同,铁路旅客乘车方案不能简单地抽象为最短路问题,需要考虑不同的旅客出行选择影响因素.本文分析了影响旅客出行路径选择的主要因素,并在简化的路网基础上构建旅客乘车网络,以总乘车时间最小、总票价费用最少、换乘次数最少、换乘距离最短、换乘间隔时间损失最小及疲劳恢复时间最短为目标函数,考虑最大换乘次数的限制,建立了铁路旅客乘车方案优化模型.本文以旅客列车时刻表为基础,设计了利用每个旅客列车时刻表的站点序列搜索出行路径的算法,该算法不需要对每个站点都进行标号,就能够得到多条可行路径,提高了路径的搜索速度.根据获得的可行路径集合,利用信息熵法确定各目标值的权重,计算各可行路径的综合目标值,利用综合目标值对可行路径进行排序,从而获得较满意的出行方案.最后,利用近期的铁路旅客列车时刻表,计算了兰州至北京及兰州至长春的铁路旅客乘车方案,计算结果表明,可以快速的得到旅客满意的出行方案.

[1] 刘雪岩.出行路线选择行为研究[D].北京:对外经济贸易大学,2006.[LIU X Y.The analysis of travelers route choice[D].Beijing:The University of International Business&Economics,2006.]

[2] BI Y,HU H P.Mathematical model of best-path planning algorithms for public transportation systems[C]//2010 International Conference on Computer Application and System Modeling,2010,V13:345-348.

[3] LIU C L.Best-path planning for public transportation systems[C]//Proc of the 5th International IEEE ConferenceonIntelligentTransportationSystems, 2002:834-839.

[4] 江南,史峰,卢红岩,等.铁路旅客乘车方案优化决策模型研究[J].铁道学报,2007,29(3):13-18. [JIANG N,SHI F,LU H Y,et al.The study on optimizationdecisionmakingmodelofpassenger traveling plan by train[J].Journal of The China Railway Society,2007,29(3):13-18.]

[5] 于冉冉.基于铁路旅客需求异质性的换乘服务方案优化研究与系统[D].北京:北京交通大学,2011. [YU R R.Optimization research of transfer services plan and aystem based on heterogeneous demand of railway passenger[D].Beijing:Beijing Jiaotong University,2011.]

[6] 刘兰芬,倪晓宇.铁路客运中转换乘模型的遗传算法研究[J].铁道运输与经济,2006,28(2):86-89. [LIU L F,NI X Y.Study on the genetic algorithm for railway passenger transferring model[J].Railway Transport and Economy,2006,28(2):86-89.][7] 王琳颖,杨浩.基于个性化需求的铁路最优换乘模型与应用研究[J].铁路计算机应用,2009,18 (12):1-5.[WANG L Y,YANG H.Study on optimal model of railway passenger transference based on individual demand and its applications[J].Railway Computer Application,2009,18(12):1-5.]

[8] 史峰,邓连波,霍亮.铁路旅客乘车选择行为及其效用[J].中国铁道科学,2007,28(6):117-121.[SHI F,DENG L B,HUO L.Boarding choice behavior and its utility of railway passengers[J].China Railway Science,2007,28(6):117-121.]

[9] 崔炳谋,马钧培,陈光伟,等.铁路旅客旅行换乘方案优选算法[J].中国铁道科学,2007,28 (6):122-127.[CUI B M,MA J P,CHEN G W,et al.Optimization algorithm of travel transfer scheme for railway passengers[J].China Railway Science,2007, 28(6):122-127.]

[10] 郭彦云.城市轨道交通有效路径问题研究[D].北京:北京交通大学,2011.[GUO Y Y. Research on problem of efficient paths for urban rail transit[D].Beijing:BeijingJiaotong University,2011.]

[11] 史峰,邓连波,黎新华,等.客运专线相关旅客列车开行方案研究[J].铁道学报,2004,26(2): 16-20.[SHI F,DENG L B,LI X H,et al.Research on passenger train plans for dedicated passenger traffic lines[J].Journal of The China Railway Society,2004, 26(2):16-20.]

[12] 孙利娟,邢小军,周德群.熵值赋权法的改进[J].统计与决策,2010,(21):153-154.[SUN L J,XING X J,ZHOU D Q.The improving of rntropy method[J].Statistics and Decision,2010,(21): 153-154.]

Route Selection for Railway Passengers: A Multi-objective Model and Optimization Algorithm

YANG Xin-fenga,LIU Lan-fena,LI Yin-zhena,b,HE Rui-chuna
(a.School of Traffic and Transportation;b.Northwest Traffic Economic Research Centre of China, Lanzhou Jiaotong University,Lanzhou 730070,China)

With an increased operating speed in Chinese railways in recent years,the number of passengers traveling by trains has been significantly increasing.The research issue is regarding how passengers select their routes when there are no direct trains.Previous studies have dealt with the route selection problem as a multi-objective optimization.The study began by setting up a transportation network which encompasses the departure and terminal stations along with important intermediate stations.Then,six key factors are analyzed and formulated using a multi-objective model,consisting of the train-running time, railway fare,transfer frequencies,distances between transfer stations,transfer interval time,and travel comfort.Furthermore,a two-phase algorithm is employed to solve the model.A rapid searching algorithm for feasible routes based on the train timetable is established,then the weight vector is assigned by introducing the information entropy to obtain satisfied routes.In the end,the two-phase algorithm is tested respectively for railway passengers from Lanzhou to Beijing(with direct trains)and from Lanzhou to Changchun(withoutdirect trains),and the results show that the proposed model and solution algorithm are efficient for obtaining satisfactory routes.

railway transportation;traveling scheme;multi objective;transfer;information entropy

U293

: A

U293

A

1009-6744(2013)05-0072-08

2012-09-27

2012-12-11录用日期:2013-01-09

国家自然科学基金项目(61164003、61064012);兰州交通大学青年基金项目(2012030).

杨信丰(1978-),男,河南省开封人,副教授,博士.

*通讯作者:xinfengyang@mail.lzjtu.cn.