“理解教材”的灵动思考与教学创新

☉湖南省常德市芷兰实验学校初中部 陈金红

教材是教师进行教学的重要资源，是专家们精挑细选出来供学生学习的材料，因此“理解教材”是教师根据学校、班级学生实际情况对教材进行创造性灵活运用、激发学生创新思考有效学习的关键.结合湘教版八（下）部分内容谈几个观点：

一、理解教材要读懂知识的内在联系

案例1：八年级下册“梯形定义”的缘起思考.

在学习梯形前已经学习了平行四边形，由平行四边形的定义：两组对边分别平行的四边形（AB∥CD、AD∥BC）是平行四边形，对“条件弱化”即只有一组对边平行（AD∥BC、AB与CD不平行），又会是什么图形呢？从而引起认知冲突，引出课题：梯形.

受上述定义缘起“平行四边形条件弱化”的启发来思考梯形的第二个定义.先由“一组对边平行且相等的四边形也是平行四边形”（AD∥BC、AD=BC），抛出问题：如何弱化？不难发现，依据梯形的定义必须有一组对边平行即需保留AD∥BC，故条件弱化的对象是AD=BC变为AD≠BC，从而得出“AD∥BC、AD≠BC”，能否作为梯形的第二定义？并挑逗、激发学生的理性思考，即由“AD∥BC、AD≠BC”化归出“AD∥BC、AB与CD不平行”即可.因由AD∥BC、AB∥CD即是平行四边形了，故有AD=BC，此时与已知AD≠BC矛盾了，即“一组对边平行且不相等的四边形”是梯形的自然产生，且从中学到了“问题是怎么提出的”科学有效的探思方法.

二、理解教材要尽力找出一条线索主线，统领相关内容体系

案例2：八年级下册平行四边形一章内容多、繁、杂，如何有效“穿针引线”？

笔者的方法是：充分利用湘教版的“变换”特点，由“任意三角形绕一边中点旋转180°后与原图形组成一个平行四边形”结论出发，依次按边、按角、按边角条件不断强化，引出课题：菱形、矩形、正方形.

具体做法：从“边条件强化”，一般三角形变为等腰三角形，绕底边中点顺（或逆）时针旋转180°后与原图形组成一个平行四边形吗？为什么？此平行四边形还有何特点？得出“一组邻边相等的平行四边形”是菱形的课题！再依次从“三大方面”（定义、性质、判定）、“四条线索”（边、角、对角线、对称性）等效仿平行四边形，展开对菱形的学习.

从“角条件强化”，一般三角形变为直角三角形，绕斜边中点顺（或逆）时针旋转180°后与原图形组成一个平行四边形吗？为什么？此平行四边形还有何特点？得出“一个内角为直角的平行四边形”是矩形的课题！受菱形单元学习的启发，也依次从“三大方面”（定义、性质、判定）、“四条线索”（边、角、对角线、对称性）等方面展开对矩形的学习.

最后从“边和角条件同时强化”，一般三角形变为等腰直角三角形，绕斜边中点顺（或逆）时针旋转180°后与原图形组成一个平行四边形吗？为什么？此平行四边形还有何特点？得出“一组邻边相等、一个内角为直角的平行四边形”是正方形的课题！受菱形、矩形单元学习的启发，也依次从“三大方面”（定义、性质、判定）、“四条线索”（边、角、对角线、对称性）等展开对正方形的学习.

显然，按上述方式学习条理清晰、方向明确、思路自然，类比探究科学、顺利、流畅，对学生逻辑类比学习方法做了一个非常有效的铺垫和示范.

三、理解教材要创造性地引出、发现、“证明”结论

案例3：由“任意三角形绕一边中点旋转180°后与原图形组成一个平行四边形”结论出发，经历图1→图2→图3→图4可创造性地提出、引导、“证明”三角形的中位线定理.

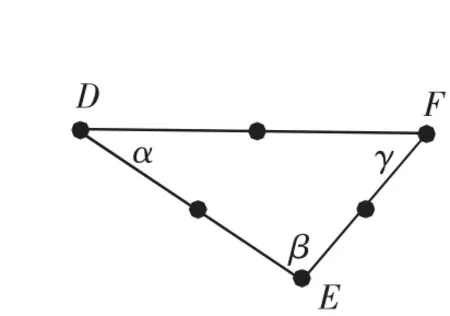
图1

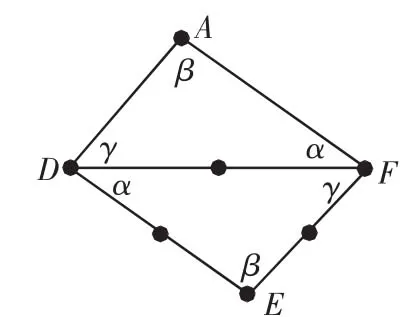
图2

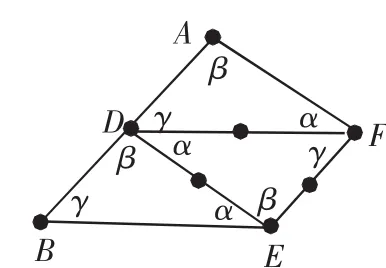
图3

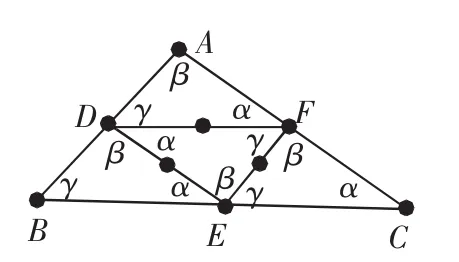
图4

从而打破了三角形中位线定理是通过测量、猜想、提出、全等论证的长久的思维定势，创造性地引出、发现、甚至论证的新方法和新思路，更凸显引进现代几何变换数学思想的无穷魅力与价值，更是创造性地使用教材的典范.

四、理解教材要挖出与重组教材中能让学生灵动的素材

案例4：多边形的内角和定理的证明.

先引导学生从一个顶点（如点A）出发引对角线，转化成三角形的方法（书上的）；再从“运动的观点”出发，让学生思考：点A还可以是什么位置？依次得出点O在边上、在多边形内部、在多边形外部三大类情况.

点O“在边上、在内部”这两种情况很快解决了；但点O在外部时，出现不同的图形、产生了争执；出现了“灵动点”：即在学生中出现了下面三种类型图，图5、图6、图7.

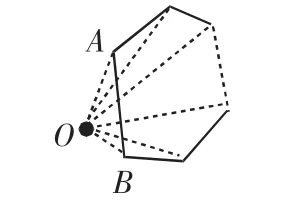
图5

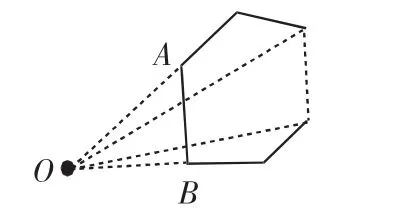
图6

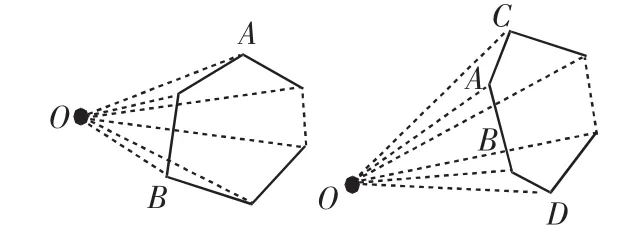
图7

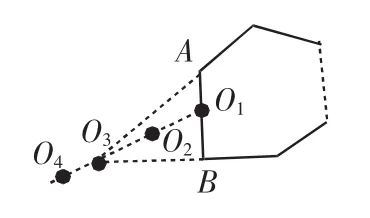
图8

此时，笔者发问：还有其他可能吗？如何统一起来？你是如何想到的？互动一段时间后，由“观察物体”视角不同观启发出：运动透视观即A→O1（AB边上点）→到达AC与BD延长线的交点前的O2点→O3点（AC与BD延长线的交点）→O4点.（如图8）

在进一步的试证过程中发现，有一种情形（如图9）证明的烦琐程度高一些.互动揭示出：点O除了与AC、AB、BD三边共构成n-3个三角形的度数，还需加上以点A、点B为顶点的内角度数，再减去混进来的角的度数.

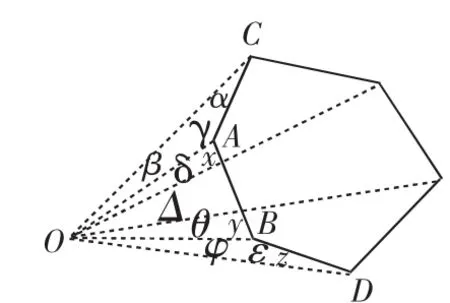
图9

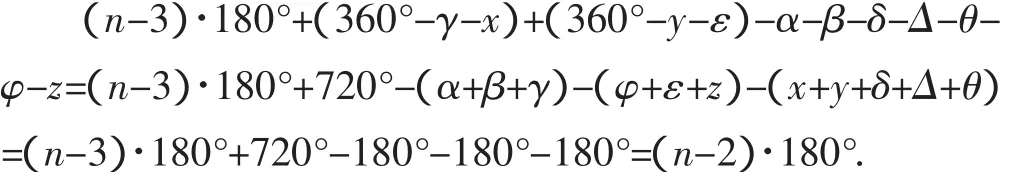
完成上述工作后，从学生的神态看出，既有惊奇，更有一种伟大发现后的得瑟和自耀.更是冲破了资料上的笼哄：点在多边形外只给出了一种不明晰的证法，从而感到自我创举的喜悦.

案例5：分式的乘除法运算，学生经常出现符号、系数、结果问题.

对策：先重组教材与上相关例题，集中练习，再回头体会、提炼出“三化”观：符号“正化”（分子、分母首项系数）、系数“整化”（分子、分母首项系数）、结果“简化”（分子、分母不含公因式）.并认识到原理都是分式的基本性质，从而避免对结果像“无头苍蝇”式乱奔，可见有机组合“易错点”问题素材是关键.

案例6：梯形相关计算，辅助线的使用是难点.

对策：先通过知识的学习，再提炼出五个重要典型图，即图10～图14.

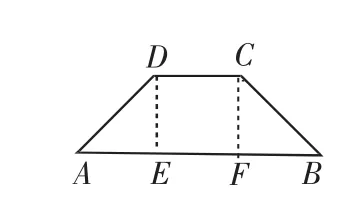
图10

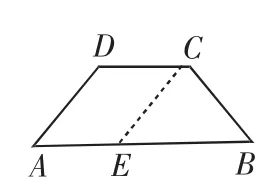
图11

图12

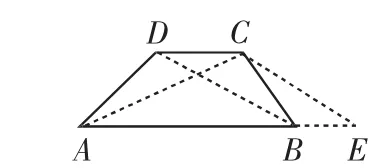
图13

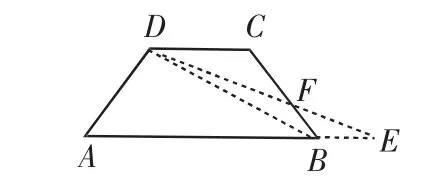
图14

课堂上，在做第109页练习1“在等腰梯形ABCD中，AB∥DC，DE是它的高，设∠A=60°，DA=4、DC=3，求下底AB的长”时，学生表现出了强烈的表现欲，分别利用图10、图11、图12给出不同的解法，显示了方法的灵动和思维的灵活性.

更表现出在接下来学习等腰梯形的判定方法时，学生自觉地运用上面典型图形给出了多种不同的证法，显然这来自于五图挖掘而带来的灵性与活力.

五、理解教材要通俗化、本质化教学内容

案例7：《异分母分式的加减法》第一课时教学片段.

师：最简公分母90是如何找到的，能否用横式表达的方式去发现之？

众生：互动议论.

生2：（极度兴奋）90实质是6和45分解质因数后，由所有的质因数及相同质因数的最高次数来产生的.

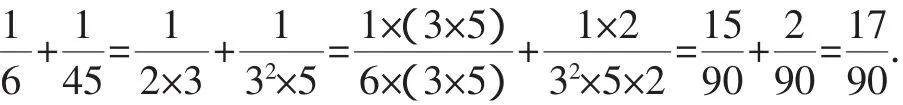
师：太好了，把计算的过程“淋漓尽致”地表现出来了！最简公分母实质是所有分母分解质因数后，由所有的质因数及相同质因数的最高次数来产生的.

生4：实质是把2用字母a、3用字母b、5用字母c替换的结果.

生5：通过类比，很容易得出最简公分母是ab2c，即包含分母因式中所有字母因式、相同字母因式的最高次.

生6：最简公分母是90ab2c.

生7：即最简公分母是“分母系数的最小公倍数、分母因式中所有字母因式、相同字母因式指数的最高次”来构成的.（下略）

显然，从熟悉的“异分母的分数加减法”公分母的确定“的本质挖掘”类比到“异分母分式的加减法”公分母的确定“清新、自然”更本质！凸显学习的是“理解的数学”而不是机械模仿的套路！有效提高了思维的灵性和活力.

教师“理解教材”的目的是让学生“理解数学”，“理解教材”先要理解数学．理解数学就是要了解数学概念的背景，掌握概念的逻辑意义，理解内容所反映的思想方法，把握概念的多元联系表示，挖掘数学知识所蕴含的科学方法、理性精神等价值观资源．教师再把“学术形态的数学”结合教材课题、学生实际转换成“教育形态的数学”，也就是“教材数学、学生数学”，因此“理解教材”是教好数学、学好数学的前提与关键.

1.义务教育课程标准实验教科书（初中数学）.长沙：湖南教育出版社，2012.

2.陈金红.在自然拓展中拔高案例解读［J］.中学数学（下），2013（4）.

3.陈金红.处理教材要“大气”地实践与思考［J］.教育科学论坛，2010（10）.