关注“直L型”图形模型 重视通法的解题功能
☉宁夏回族自治区中卫市沙坡头区宣和镇张洪学校 张 宁
一、基本模型的提炼
例1(2009年深圳)如图1,矩形ABCD中,由8个面积均为1的小正方形组成L型模板按图1所示放置,则矩形ABCD的周长为______.
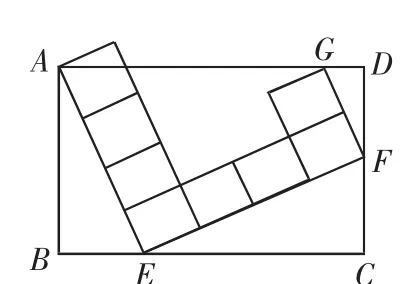
图1
解析:易知小正方形的边长为1,所以AE=EF=4,FG=2.
因为∠AEF=90°,所以∠AEB+∠FEC=90°.由∠ABE=90°,得∠BAE+∠AEB=90°.所以∠FEC=∠BAE.又因为∠ABE=∠FCE=90°,AE=EF=4,所以△ABE≌△ECF,所以BE=CF,AB=EC.
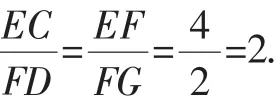
令DF=x,则EC=2x,AB=2x.所以FC=DC-DF=2x-x=x,所以BE=x.
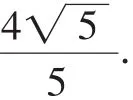
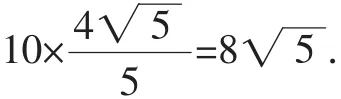
点评:本题虽然是一道填空题,但它所涉及的知识点比较多,主要考查全等三角形的判定与性质、相似三角形的判定与性质、矩形的性质、勾股定理等知识点.本题以矩形和直角三角形为背景,构思巧妙,设计新颖,具有较强的探索性,全面考查了学生综合运用所学知识分析问题和解决问题的能力.它的解法具有广泛的代表性,是解决同类问题的通法.
近几年各地中考试题中经常出现以图1为模型命制的中考试题,由于它的形状类似于字母“L”,不妨称这种基本图形为“直L型”图形,它是中考命题中一个重要的数学模型,这种模型的通性通法对解决同类问题具有一定的导向作用,在教学中非常有必要引导学生关注“直L型”图形模型,使学生重视通法的解题功能,本文以近两年各地中考试题为例,说明“直L型”图形模型的通法在解题中的应用.
二、“直L型”图形的性质
1.直角梯形中的“直L型”图形的性质
如图2,直角梯形ABCD中,AB∥CD,∠BCD=90°,AB=a,CD=b,BC=c. 若在BC上存在直角点M,使AM⊥DM,则:
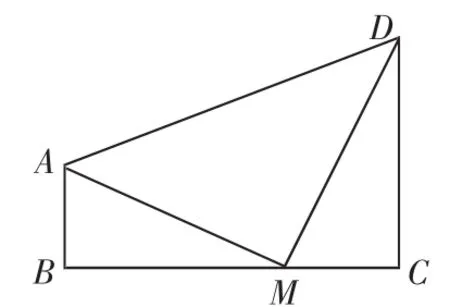
图2
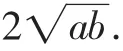
证明:设BM=x,则MC=c-x.
由AM⊥DM,知∠AMD=90°,所以∠AMB+∠DMC=90°.
因为∠ABM=90°,所以∠BAM+∠AMB=90°.
所以∠DMC=∠BAM.
又因为∠ABM=∠DCM=90°,所以△ABM∽△MCD.
所以x2-cx+ab=0.
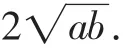


2.矩形中的“直L型”图形的性质
如图3,在矩形ABCD中,AD=a,AB=b,点M在BC边上,连接AM、DM,∠AMD=90°,点M为直角点.则:
①△ABM∽△MCD;②a≥2b.
证明:设BM=x,则MC=a-x.
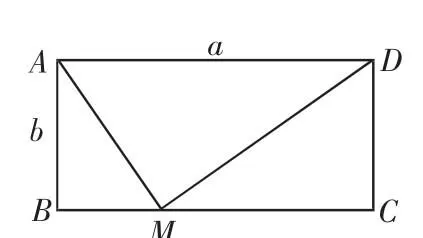
图3
因为∠AMD=90°,所以∠AMB+∠DMC=90°.
因为∠ABM=90°,所以∠BAM+∠AMB=90°.
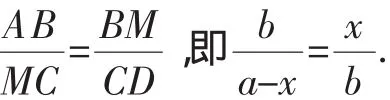
所以x2-ax+b2=0.由Δ=a2-4b2≥0,知a≥2b.即当BC上存在点直角点M,使AM⊥DM时,a≥2b.反之易知:若a≥2b,则BC上存在直角点M,使AM⊥DM.
以上得出的“直L型”图形的性质及性质的证明方法在解决同类问题中有着广泛的应用.
三、“直L型”图形模型在解中考题中的应用
例2(2012年浙江省嘉兴市)在平面直角坐标系xOy中,点P是抛物线y=x2上的动点(点P在笫一象限内).连接OP,过点O作OP的垂线交抛物线于另一点Q.连接PQ,交y轴于点M.作PA⊥x轴于点A,QB⊥x轴于点B.设点P的横坐标为m.

①求线段OP的长和tan∠POM的值;
②在y轴上找一点C,使△OCQ是以OQ为腰的等腰三角形,求点C的坐标.
(2)如图5,连接AM、BM,分别与OP、OQ相交于点D、E.
①用含m的代数式表示点Q的坐标;②求证:四边形ODME是矩形.
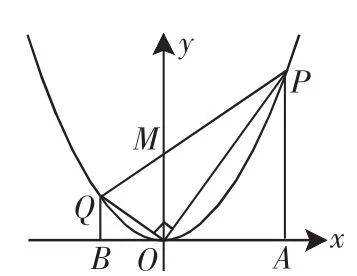
图4
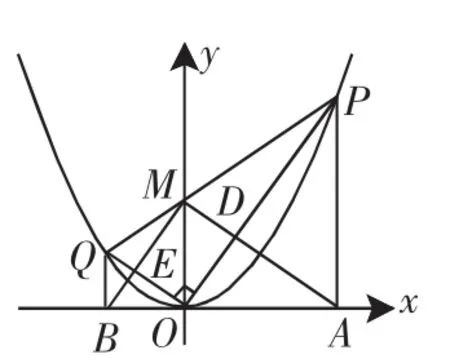
图5
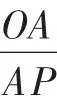

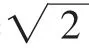
因为PA⊥x轴,所以PA∥MO.

②设Q(n,n2).
因为tan∠QOB=tan∠POA,

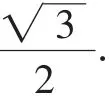

当OQ=CQ时,C3(0,1).
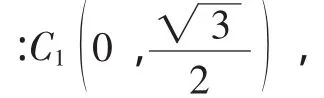
(2)①P(m,m2),设Q(n,n2).


②设直线PQ的解析式为y=kx+b.
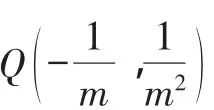
解得b=1.
所以M(0,1).
所以∠MAO=∠QOB.
所以QO∥MA.
同理,可得EM∥OD.
所以四边形ODME是平行四边形.
又因为∠EOD=90°,所以平行四边形ODME是矩形.
点评:本题是一道几何代数综合题,主要考查一次函数、二次函数、勾股定理、相似三角形的性质与判定、矩形的判定及方程思想、分类讨论、特殊到一般的数学思想等的综合应用.解题的关键是灵活应用所学知识,求出关键点P、Q、M的坐标.本题中的“直L型”图形是梯形中的“直L型”图形,在求点Q的坐标时要充分利用“直L型”图形中证明三角形相似的方法.
例3(2012年四川省南充市)如图6,矩形ABCD中,AB=2AD,E为AD的中点,EF⊥EC交AB于点F,连接FC.
(1)求证:△AEF∽△DCE;
(2)求tan∠ECF的值.
分析:(1)由“直L型”图形中证明三角形相似的方法,易证△AEF∽△DCE.
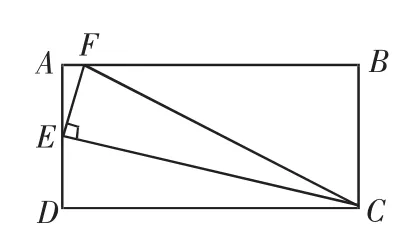
图6
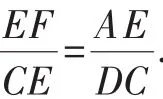
解:(1)在矩形ABCD中,∠A=∠D=90°.
因为EF⊥EC,所以∠FEC=90°.
所以∠FEA+∠CED=90°.
因为∠FEA+∠EFA=90°,所以∠EFA=∠CED.
所以△AEF∽△DCE.
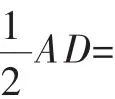
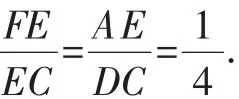
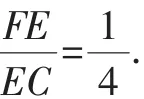
点评:此题考查相似三角形的判定与性质、矩形的性质以及锐角三角函数的定义.此题难度适中,在根据题意无法直接求得三角形的边长时,可考虑利用三角形的相似关系,利用“直L型”图形中相似三角形的证法易知△AEF∽△DCE,通过利用“相似三角形对应边成比例”的性质,结合题中的线段间的倍数关系,推得∠ECF的三角函数值,解题时还要注意数形结合思想的应用.
例4(2011年湖南省衡阳市)如图7,在矩形ABCD中,AD=4,AB=m(m>4),点P是AB边上的任意一点(不与A、B重合),连接PD,过点P作PQ⊥PD,交直线BC于点Q.
(1)当m=10时,是否存在点P,使得点Q与点C重合?若存在,求出此时AP的长;若不存在,说明理由.
(2)连接AC,若PQ∥AC,求线段BQ的长(用含m的代数式表示).
(3)若△PQD为等腰三角形,求以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式,并写出m的取值范围.
解:(1)假设当m=10时,存在点P,使得点Q与点C重合,如图8所示.
因为PQ⊥PD,所以∠DPC=90°.
所以∠APD+∠BPC=90°.
又因为∠ADP+∠APD=90°,所以∠BPC=∠ADP.
又∠B=∠A=90°,所以△PBC∽△DAP.
解得AP=2或8.
故存在点P,使得点Q与点C重合,此时AP的长为2或8.
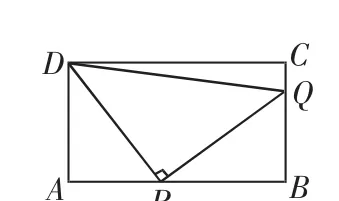
图7

图8
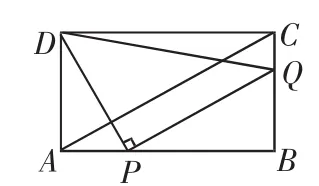
图9
(2)如图9,因为PQ∥AC,所以∠BPQ=∠BAC.
又因为∠BPQ=∠ADP,所以∠BAC=∠ADP.
又因为∠B=∠DAP=90°,所以△ABC∽△DAP.
由∠BPQ=∠BAC,∠B=∠B,得△PBQ∽△ABC.
(3)由于已知PQ⊥PD,所以只有当DP=PQ时,△PQD为等腰三角形.
由∠BPQ=∠ADP,∠B=∠A=90°,DP=PQ,得△PBQ≌△DAP.
所以PB=DA=4,AP=BQ=m-4.
故以P、Q、C、D为顶点的四边形的面积S与m之间的函数关系式为:
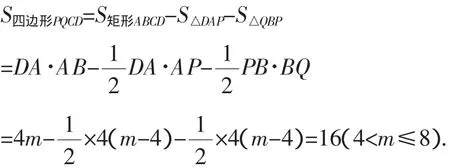
点评:本题主要考查相似三角形的判定与性质、全等三角形的判定与性质、一元二次方程的解法.问题(1)是存在型问题,解决这类问题时,首先假设存在点P,使得点Q与点C重合,然后充分利用“直L型”图形中相似三角形的证明方法说明△PBC∽△DAP,利用相似三角形的性质列出关于三角形某一边长的一元二次方程,如果方程有解,则存在满足条件的点;如果方程无解,则不存在满足条件的点.这种方法也是解决其他类型存在性问题时常用的方法.
例5 (2012年山东泰安)如图10,E是矩形ABCD的边BC上一点,EF⊥AE,EF分别交AC、CD于点M、F,BG⊥AC,垂足为G,BG交AE于点H.
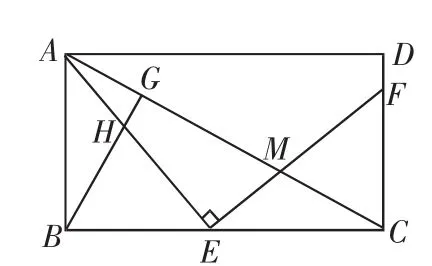
图10
(1)求证:△ABE∽△ECF;
(2)找出与△ABH相似的三角形,并证明;
(3)若E是BC的中点,BC=2AB,AB=2,求EM的长.
分析:(1)由“直L型”图形中证明三角形相似的方法,易证△ABE∽△ECF.
(2)由BG⊥AC,易证得∠ABH=∠ECM.
又∠BAH=∠CEM,即可证得△ABH∽△ECM.
(3)如图11,作MR⊥BC,垂足为R.
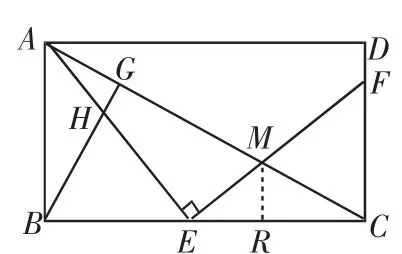
图11

解:(1)因为四边形ABCD是矩形,所以∠ABE=∠ECF=90°.
因为AE⊥EF,所以∠AEB+∠FEC=90°.
又∠BAE+∠AEB=90°,所以∠BAE=∠CEF.
所以△ABE∽△ECF.
(2)△ABH∽△ECM.
因为BG⊥AC,所以∠ABG+∠BAG=90°.
所以∠ABH=∠ECM.
由(1)知∠BAH=∠CEM,所以△ABH∽△ECM.
(3)作MR⊥BC,垂足为R.



点评:本题考查矩形的性质、直角三角形的性质、相似三角形的判定与性质以及三角函数等知识.解题时注意数形结合思想的应用,注意掌握“有两组角对应相等的两个三角形相似”定理的应用.问题 (1)中证明△ABE∽△ECF时,要充分利用“直L型”图形中证明三角形相似的方法,问题(1)也是解决后面问题的关键,所以“直L型”图形中证明三角形相似的方法在解决问题中起到了至关重要的作用,所以在教学中要特别重视通法的解题功能.
从以上中考试题可以看出,“直L型”图形的性质有着广泛的应用.它提供的证明三角形相似的方法和解题思路对解决同类问题具有一定的导向作用.如果教师在中考复习教学中设计一节专门探究“直L型”图形性质的数学活动课,引导学生关注“直L型”图形模型,通过师生共同探究“直L型”图形的性质,一定能激发学生学习数学的兴趣,让学生掌握“直L型”问题中证明三角形相似的方法和解题思路,使学生不仅学会解答与“直L型”图形有关的中考题,引导学生重视通法的解题功能,而且能有效提高学生应用所学数学知识分析问题和解决问题的能力.

