压轴题的解题利器——谈旋转在几何中的应用

☉广东省珠海市实验中学 胡洁慧

初中几何中的三大图形变换：平移、对称、旋转.其中，旋转是非常重要的辅助线作图技巧，在很多几何压轴题中多次出现，方法独特，不可忽视.旋转的特点很明显，经常用在等腰三角形或正方形中，条件明显，思路单一.在学习旋转的过程中，首先，要掌握旋转的基本感念和基本性质，掌握旋转前后的结构变化；其次，要掌握旋转应用的环境，什么情况下使用旋转，如何旋转，如何判断旋转后的结构是否是我们需要的结构.

下面是旋转的基本概念和旋转的基本性质：

图1

旋转的基本概念：如图1，把一个图形绕着点O转动一个角度的图形变换叫做旋转.其中点O叫做旋转中心，转动的角叫做旋转角.如果图形上的点A经过旋转变为点E，那么这两个点叫做这个旋转的对应点，线段OA经过旋转变为线段OE，那么这两条线段叫做这个旋转的对应边.

旋转的基本性质：

①对应点到旋转中心的距离相等；

②对应点与旋转中心所连线段的夹角等于旋转角；

③旋转前后的图形全等.

在几何压轴题中，旋转的应用非常重要，下面就常见的几种类型问题来说明旋转的重要性.

一、求角度问题

例1 如图2，已知在Rt△ABC中，∠ABC=90°，AB=BC，P为三角形内一点，且AP∶BP∶CP=1∶2∶3，求∠APB的度数.

分析：首先判断出∠APB一定是一个特殊钝角，根据钝角的特点，要么求它的补角，要么将钝角进行分割.不管是哪种情况，要把该角放在一个特殊的图形结构当中去.观察发现，题设中的条件是一个等腰直角三角形，因此，可以考虑旋转的变换.

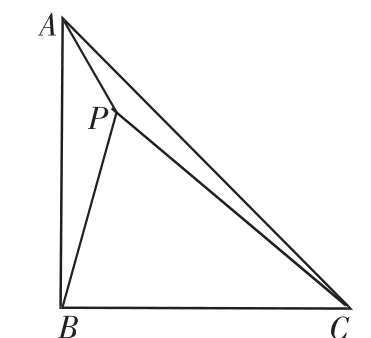
图2

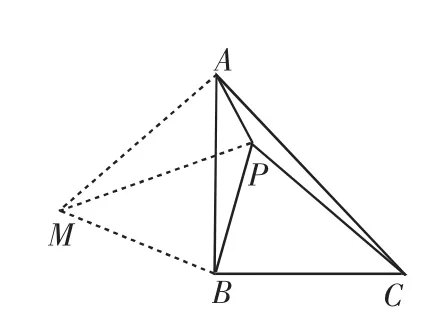
图3

解：如图3，过B作BM⊥BP，且BM=BP，连接MP，MA.

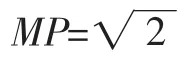
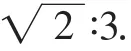
所以AM2=MP2＋AP2.

所以∠MPA=90°.

所以∠APB=135°.

总结：求角度的问题一般是要转化为特殊的三角形结构，而出现三角形的变换借助于旋转.旋转应用的环境是等腰直角三角形，在这种环境中经常使用旋转，注意掌握.

二、求线段长度问题

（1）求线段BD的长度；

（2）求四边形ABCD的面积.

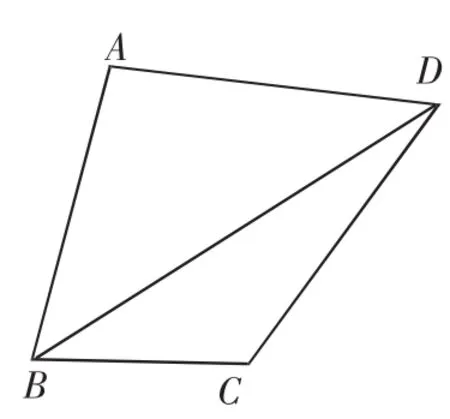
图4

分析：通过观察发现，题设中有线段长度，角度，线段相等.其中，线段长度不是一个重要条件，往往用在计算过程当中，角度条件是个特殊条件，不过，通过尝试发现，不是突破口，最后，线段相等是个关键，常用于旋转，可以尝试一下.

解：（1）如图5，将△BAD绕着D点逆时针旋转60°，得到△ECD，连接BE.

由图可知，A点对应点为C点，B点对应点为E点，

所以CE=AB=2，∠A=∠DCE.

因为DB=DE，∠BDE=60°，

所以△BDE为等边三角形.

在四边形ABCD中，∠A＋∠ABC＋∠BCD＋∠CDA=360°，

又因为∠BCD＋∠BCE＋∠ECD=360°，

所以∠BCE=∠ABC＋∠ADC=75°＋60°=135°.

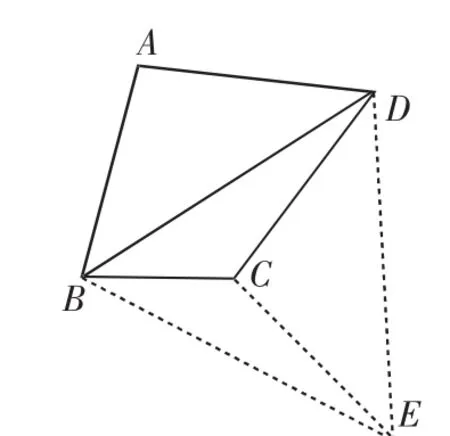
图5

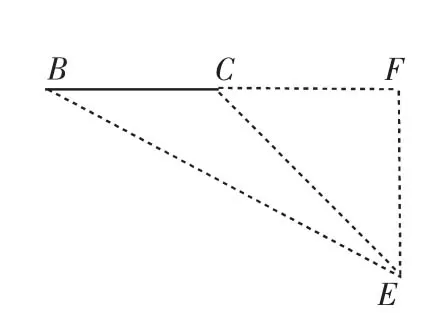
图6

如图6，∠BCE=135°，过点E作EF⊥BC交BC的延长线于F，所以在Rt△CED中，EC=2.

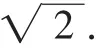
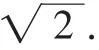
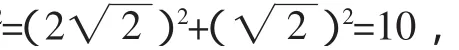
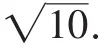
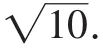
（2）由图5可知，S四边形ABCD=S△BED.

总结：当出现有公共端点的两条线段相等的条件时，这时，要注意旋转的应用.求图形的面积的时候，对于不规则四边形情况，往往变换图形，使得变换为规则图形或规则三角形，进而求解其面积.

三、求长度最小值问题

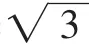
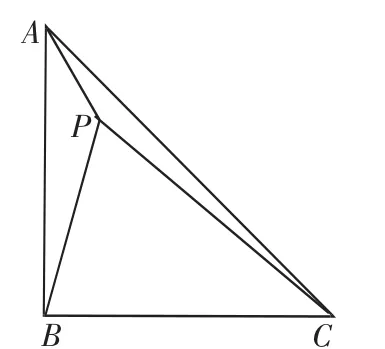
图7

分析：旋转的一个重要用法，就是解决三条线段和的最小值问题.目的是把有公共端点的三条线段转化到一条折线上，利用两点之间线段最短的理论来处理.

解：如图8，将△APB绕着点A顺时针旋转60°，得到△AED，连接EF，DB.

由旋转可知，AD=AB，∠DAB=60°，

所以△ADB为等边三角形.

同理，△AEP也为等边三角形.

所以DE=BP，EP=AP.

所以AP＋BP＋CP=DE＋EP＋PC.

当D、E、P、C四点共线时，DE＋EP＋PC取得最小值.

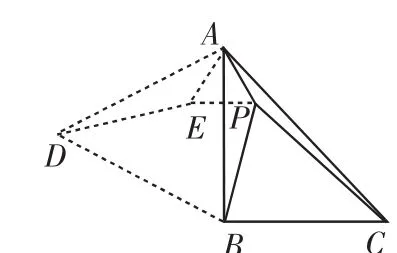
图8

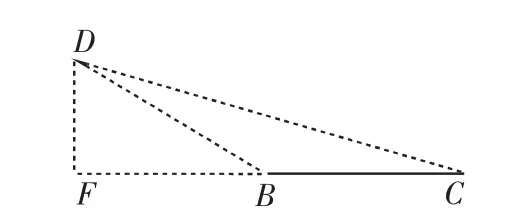
图9

如图9，过点D作DF⊥BC交CB的延长线于F，

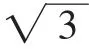
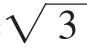
所以DC=

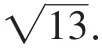
总结：此类问题的突破点在于结论，三条线段之和的最小值.通过旋转的变换，图形中出现了两个等边三角形的结构，将有公共端点的三条线段转换为在一条折线上，利用两点之间线段最短的性质来判定.最后出现了一个特殊角的三角形，利用勾股定理来求线段的长度.

以上是运用旋转的几种常见题型，进而出现了特殊的图形结构，产生新的等量关系，把条件和结论有效地结合起来，从而达到解决问题的目的.