四边形中的蝴蝶定理

☉江苏省连云港市新海实验中学 赵 渊

蝴蝶定理 过圆的弦AC的中点I，作两条不同的弦EF、HG.如果EG、HF分别交AC于点M、N，那么IM=IN.

蝴蝶定理是初等几何中的近代名题之一，它于1815年在西欧出版的杂志《男士日记》上问世，它引起了众多数学爱好者的关注，其中有些人给出了简单、优美的证明，还有一些人给出了各种不同的图形变式以及一般化结论.特别地，有人在圆中对蝴蝶定理作了推广，并运用面积的方法进行证明：

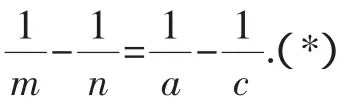
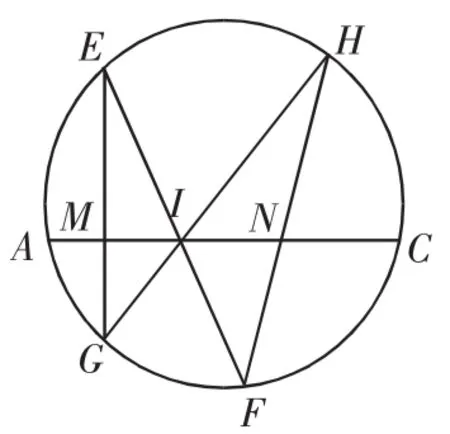
图1

本文中我们将用类似的方法证明四边形中的蝴蝶定理.

我们先来看有关三角形面积的一些性质.

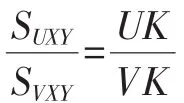
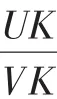
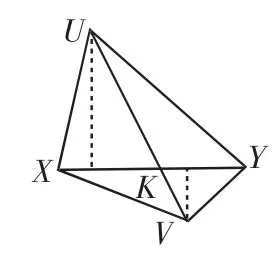
图 2（1）

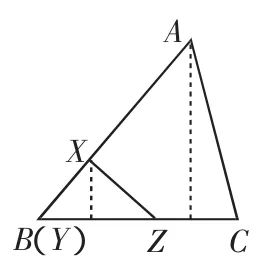
图 2（2）

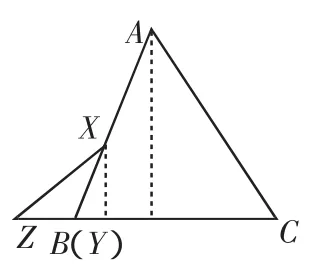
图 2（3）

我们将蝴蝶定理推广到四边形中：

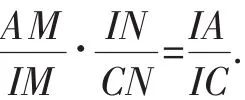
证明：如图3所示，我们发现12对三角形，每一对三角形具有公共的边或公共的角或相等的角.运用三角形面积的两个性质，我们有：

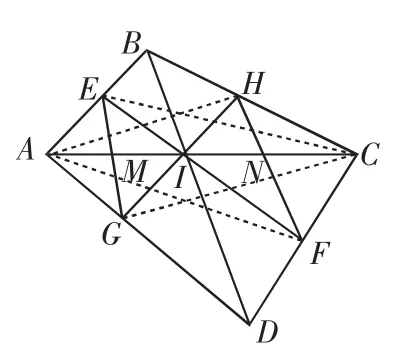
图3

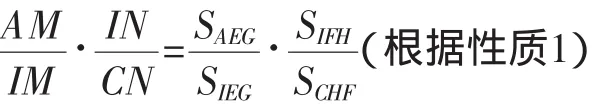
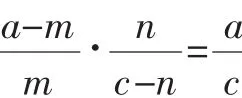
1.周春荔.蝴蝶定理——研究性学习的一个好课题［J］.数学通报，2004（1）.

2.肖秉林.蝴蝶定理的另一呈现形式［J］.数学通报，2006（5）.

3.郝志刚.花蝴蝶定理［J］.数学通报，2010（4）.