入匝道系统元胞自动机模型的换道规则研究

朱昶胜，马玉婷，王庆荣

1.兰州理工大学 计算机与通信学院，兰州 730050

2.兰州理工大学 电气工程与信息工程学院，兰州 730050

3.兰州交通大学 电子与信息工程学院，兰州 730070

入匝道系统元胞自动机模型的换道规则研究

朱昶胜1，马玉婷1，王庆荣2，3

1.兰州理工大学 计算机与通信学院，兰州 730050

2.兰州理工大学 电气工程与信息工程学院，兰州 730050

3.兰州交通大学 电子与信息工程学院，兰州 730070

1 引言

交通问题一直是困扰大中城市发展的“瓶颈”之一。匝道在实际交通中，一直是连接高架道路系统和地面道路系统的“桥梁”，作为重要的交通瓶颈之一，匝道在城市立体交通网络中起着举足轻重的控制和调节作用。因此，匝道的研究对社会经济和日常生活的发展具有非常重要的作用。国内外不少学者对匝道入口处的交通流开展了多方位细致的研究，并取得了一些成果。

在交通过程中可以观察到的非平衡的相变，交通阻塞的行程与消散，时走时停波，“幽灵”式交通堵塞，亚稳态区域和同步交通等非线性现象[1]，在匝道系统中也可观察到其中的一些现象。为了更好地解释观测到的现象，人们建立了各种交通流模型，然后发现元胞自动机理论能更好地描述交通流模型的非线性现象及特性。近年来，基于元胞自动机理论的交通流模型越来越多地应用于交通流模拟研究中。Nagel和Schreckenberg[2]提出NaSch模型之后，NaSch模型就被应用于TRANSIMS项目对运输系统进行模拟[3]，以及发布在互联网上的杜伊斯堡市交通的在线实时模拟[4]，模拟结果证实其可以重现真实的交通流现象。

为进一步研究驾驶员的行为，出现了一些改进的NaSch模型。这些模型研究了由于前车的阻挡而采取的刹车行为的影响[5]，车辆自身速度对随机延迟概率的影响[6]，车头间距对随机慢化概率的影响[7]，前车虚拟速度对驾驶员行为的影响[8]，车辆之间的相对运动[9-10]和车流密度对驾驶员行为的影响[11]，安全驾驶需求对驾驶员行为的影响[12]，混合车辆之间的速度差异及驾驶员敏感程度的不同的影响[13]，驾驶员不确定性敏感预期行为的影响[14]，随机慢化优先和车辆间距预测值的影响[15]，驾驶员不同特性的影响[16]，以及驾驶员的记忆效应和当前环境的影响[17]等。这些研究都是从驾驶员行为的角度出发，模拟驾驶员在实际交通中的刺激、判断和决策等一系列心理和生理活动。

而在匝道研究的过程中，已经有的匝道模型包括主道为单车道的信号灯匝道模型[18-19]和主道为双车道的信号灯匝道模型[20]，得出的结论是：信号灯控制的双车道入匝道系统能模拟出比信号灯控制的单车道入匝道系统更加符合实际的交通流特性。还研究过一种新的匝道通行控制规则——交替通行控制[21]。交替通行控制能引导和指示车辆按“左侧车道——右侧车道——左侧车道”的顺序逐辆一次通行，达到按1∶1的比例交通通行的目的，这种控制规则能在一定程度上减弱主道与主道之间相互的瓶颈效应。

本文在NaSch模型基础上对主道为单车道的匝道系统进行改进，更强调匝道车辆在进入主道的换道过程中驾驶员的行为，考虑了换道时候的安全距离，探讨了不同换道行为对匝道交通流的影响。结果显示安全距离为零的换道行为对匝道系统的交通流具有重要影响，本研究具有一定的实际意义。

2 换道规则

上匝道车流在与高架路外侧车道车辆交汇时有较长的加速车道，从上匝道驶入高架道路的车辆，要视主干线外侧车道车流中适当间隙而进入、合流。由于上匝道车辆的合流对主干线交通的影响主要是在高架道路的外侧车道上，因此可以忽略内车道。将上匝道与主干道合流处的模型简化，如图1和图2所示。

图1 入匝道的实图和示意图

图2 上匝道与主干道合流处的简化图

在图2中，为了清晰地描述模型，将主干道分为两个部分，匝道上游的主干道部分设定为道路A（点状阴影处），匝道下游的主干道部分设定为道路B（斜线阴影处）；匝道包括加速道部分定义为道路C（无阴影留白处），车辆的运行方向为从左到右（在本文中车辆默认从左向右行驶）。

加速车道处产生的交通冲突问题，实际上是在固定的位置处车辆变换车道的问题，即入口匝道车辆在加速车道的有限长度内变换车道，然后达到进入主线行驶的目的。因此需要确定合理的换道规则。假定加速车道上的车辆称为车辆1，与其相对应的主干道平行位置上的后车和前车分别称为车辆2和车辆3，各车辆的位置和速度均用x和v表示。

以下是匝道系统中可能出现的四种换道规则，具体设定如下：

换道规则1如果车辆1满足条件x1-x2＞0且x3-x1＞0，它就会以概率p1=pex变换车道至主干道。这种规则对应于驾驶员冒进的换道行为，他们总是积极地换道，主道稍有空隙则从加速车道换道至主道。文献[21]中的第一种模型即采用的是此种换道规则。

换道规则2如果车辆1满足条件x1-x2＞0且x3-x1-1＞0，它就会以概率p1=pex变换车道至主干道，这种换道规则要求换道车辆在进入主道后，距离前车至少有一个车身的安全距离才会改换车道。

换道规则3如果车辆1满足条件x1-x2-1＞0且x3-x1＞0，它就会以概率p1=pex变换车道至主干道，这种换道规则要求换道车辆在进入主道后，距离后车至少有一个车身的安全距离才会改换车道。

换道规则4如果车辆1满足条件x1-x2-1＞0且x3-x1-1＞0，它就会以概率p1=pex变换车道至主干道。该规则对应于保守的驾驶者的换道行为，这种驾驶者最注重行车安全，只有确定换道后和主道上的前车和后车各至少有一个车身的安全距离的时候，他们才会开始换道。

图3 四种换道规则

pex＜1是指由于驾驶员的心理状态和行驶习惯各不相同，满足上述条件的车辆不一定全部换道。为了简单起见，本文设定这里的p1=pex=1，也就是满足换道条件的车辆全部会改变车道。

3 模型具体设定和数值模拟

数值模拟的高架路段主干道的长度L为750 m，将其等分为100个格子（即元胞），相当于每个格子的大小对应的实际道路长度是7.5 m，上匝道长度为50个格子，加速车道占据10个格子，与主干道的第51～60个格子相平行。每一个格点最多仅能由一个车辆所占据。假设主干道和上匝道的车辆具有相同的最大速度vmax=5，相当于实际车速135 km/h。

NaSch模型考虑了车辆加速、减速、随机慢化和车辆位置更新四个过程，车辆速度vn∈[0，vmax]。xn(t)表示第n个车辆在t时刻的位置；vn(t)表示第n个车辆在t时刻的速度；vmax表示最大速度；P表示车辆延迟刹车概率；gapn(t)表示第n个车辆在t时刻与前方紧邻的车辆的间距，gapn(t)=xn+1(t)-xn(t)-1。

根据NaSch模型，车辆状态演化的更新规则如下[2]。

（1）加速过程：vn→min(vn+1，vmax)，对应于现实中司机期望以最大速度行驶的特性。

（2）减速过程：vn→min(vn，gapn)，驾驶员为了避免和前车发生碰撞而采取减速的措施。

（3）随机慢化：以概率P，vn→max(vn-1，0)，对应于现实中由各种不确定因素（如路面状况不好，驾驶员的不同心态等）造成的车辆减速。

（4）位置更新：xn→xn+vn，车辆按照调整后的速度向前行驶。

模型采用的开口边界条件设定如下：假设道路A和道路C最左边的元胞对应于x=1，并且A和C的入口端包含vmax个元胞，也就是说，车辆可以从元胞(1，2，…，vmax)进入到A和C中。在t→t+1时刻，当道路上的车辆更新完成后，监测A、C上的尾车位置和B上的头车位置，分别设定为xAlast、xClast以及xBlead。当xAlast(xClast)＞vmax时，一速度为vmax的车以概率a_m(a_r)进入元胞min[xAlast(xClast)-vmax，vmax]。在道路B的出口处，当头车位置xBlead＞L_m（L_m定义为主干道的总长度），头车从系统中消失，紧随其后的的第二辆车成为新的头车。

关于加速道上车辆的换道时机，一般是把每个时间步划分为两个子时间步：在第一个子步内，车辆按照换道规则进行换道；在第二个子步中，车辆在两条车道上按照单车道的更新规则进行更新[22]。

N为分布在道路长为L上的车辆数，vi是第i辆车的速度，计算公式为：

最理想情况下，在匝道模型的出口端，一个时间步可以有一辆车出流，这代表理想状态下的匝道系统的最大流量是1 car/s，即3 600 car/h。所以当q=0.1时，代表该匝道路段1 h内通行车辆为3 600×0.1=360辆。

实际模拟中，选取P=0.25，每一次运行取21×104时间步进行数值模拟，开始的t0=104时间步不进行统计，以便消除暂态的影响，以后的T=20×104的每一时间步中对vi(t)进行统计，将经过20×104时间步的速度进行时间平均，这样就得到了每一次运行的平均速度V。

首先通过数值模拟得到了匝道系统的总流量。图4为匝道模型在四种不同的换道规则下，系统总流量随车辆产生概率产生的变化。图4（a）中匝道车辆产生概率a_r固定为0.2，图4（b）中主道车辆产生概率a_m固定为0.2。用J1、J2、J3、J4分别表示在四种换道规则下系统的总流量。

由图4（a）可得，在匝道车辆产生概率a_r固定为0.2的情况下，当主道车辆产生概率a_m＜0.3时，四种换道规则下，系统总流量大致上保持一致，J1=J2=J3=J4且随着a_m的增加而线性增加。当a_m＞0.3时，匝道系统的总流量逐渐达到饱和状态，四种换道规则中换道规则4的优势开始显示出来，J4取得最大值。

由图4（b）可得，在主道车辆产生概率a_m固定为0.2的情况下，当匝道车辆产生概率a_r＜0.3时，四种换道规则下，系统总流量J1=J2=J3=J4且随着a_r的增加而线性增加。当a_r＞0.3时，随着匝道上产生的车辆越来越多，换道规则1下，匝道上车辆的积极换道行为使得匝道系统总流量大大降低，而换道规则4则仍然保持其优越性，在四种换道规则中，明显有J4＞J2＞J3＞J1。

为了直观地比较四种换道规则对匝道交通流的影响，考察了四种换道规则下，匝道系统各个部分在不同的车辆产生概率下的流量。图5给出了路段A、B和C的流量JA、JB和JC。

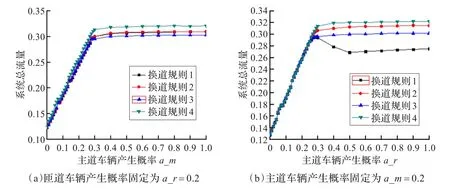
图4 匝道系统的总流量在四种换道规则下的区别

图5（a）、（b）显示，当匝道上车辆产生概率固定为0.2，主道车辆产生概率小于0.3左右时，四种换道规则下，路段A和路段B上的流量大致是一样的。随着主道车辆产生概率的增加，匝道系统逐渐达到饱和状态，系统流量逐渐稳定，换道规则4则显示出其优越性，在四种换道规则中，换道规则4使路段A和路段B都得到最大的流量稳定值。图5（c）显示，当匝道上车辆产生概率固定为0.2，主道车辆增多时，在换道规则1下，匝道车辆的积极换道行为不但不能使匝道路段C的流量得到提高，反而使匝道段流量成为四种换道规则中的最低。

图5（d）、（e）、（f）显示，当主道上车辆产生概率固定为0.2时，随着匝道上产生的车辆逐渐增多，在换道规则1下，匝道车辆的积极换道行为虽然能明显增加路段C上的车流量，但是却会严重减少路段A和路段B上的车流量，路段A上的流量接近于0代表着路段A上的车辆甚至无法行驶。而换道规则4依然保持其优越性，使路段A和路段B能得到其最大的流量稳定值。

由此可知，匝道上车辆的冒进换道行为并不能提高整个匝道系统交通流量。而当匝道上车辆比较多时，冒进换道的车辆行为能造成主道上游的严重的堵塞。为了提高匝道系统的流量，保证匝道通行顺畅，应该严厉禁止匝道上车辆的冒进换道行为，鼓励车辆采取考虑安全距离的换道行为。

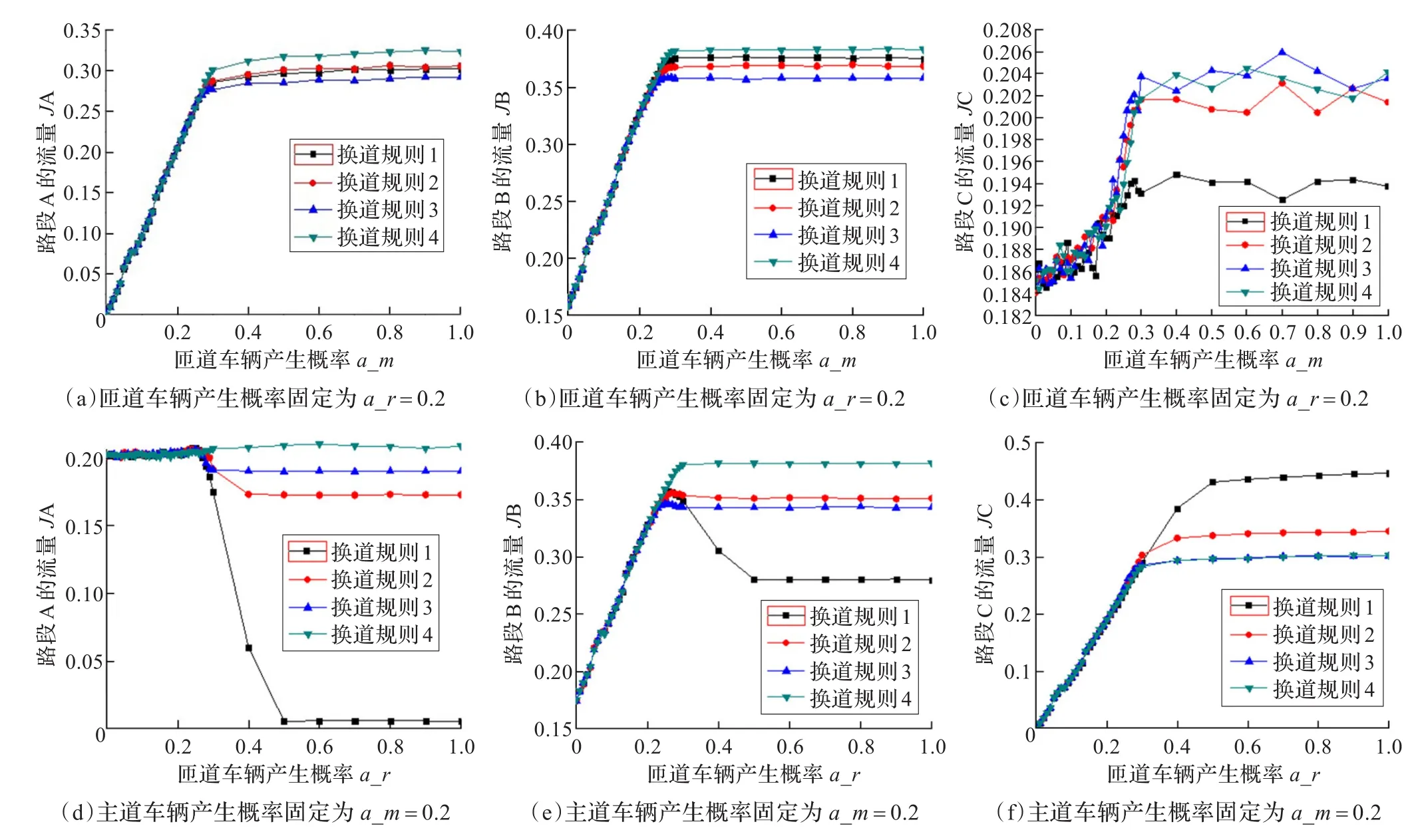
图5 匝道系统各部分在四种换道规则下的流量JA、JB、JC

4 结论

近年来，匝道交通流的研究在元胞自动机模型的辅助下有了较大的发展。本文在NaSch模型的基础上，考虑换道时候的安全距离，提出四种不同的换道规则，并对交通流进行模拟，从而展示了匝道交通流的复杂行为，证实了匝道和主道交通流的相互影响。从匝道系统各个部分的流量图可以看出：不考虑安全距离的换道规则下匝道对主道交通流的瓶颈作用明显，从而说明匝道换道行为对主道交通的重要影响。实际交通中，匝道车辆的换道行为对匝道系统的车流的作用是很大的，数值模拟表明，不考虑换道安全距离的驾驶车辆越多，匝道对主道的抑制作用就越强，而同时考虑了前后车的安全距离的换道行为能使整个匝道系统的流量达到最大的稳定值。

匝道系统上的换道规则研究并没有结束，主道为单车道的匝道模型只是一个简化模型。在主道流量较高的情况下，匝道车辆合流的并道行为一定不仅仅只影响快速路的最外侧车道，外侧车辆的行为或多或少对内侧车道也有一定的影响，但是具体的影响如何，必须进一步使用主道为双车道的匝道模型来进行模拟仿真。信号灯作为交通系统中的常见设备，对匝道交通流产生着重要的影响。如何将匝道系统上换道行为与信号灯结合起来，也是亟待研究的下一个课题。

[1]Kerner B S.Cluster effect in initially homogeneous traffic flow[J].Phy Rev E，1993，48（4）.

[2]Nagel K，Schreckenberg M.A cellular automaton model for freeway traffic[J].J Phys I France，1992，2（12）：2221-2229.

[3]Wagner P.Traffic and granular flow[M].Singapore：World Scientific，1996.

[4]OLSIM：physics of transport and traffic[EB/OL].[2011-10]. Essen：University of Duisburg，http：//traffic.comphys.uni-duis-burg-essen.de.

[5]Benjamin S C，Johnson N F，Hui P M.Cellular automata models of traffic flow along a highway containing a junction[J].Journal of Physics A：Mathematical and General，1996，29（12）：3119-3127.

[6]Barlovic R，Santen L，Schadschneider A，et al.Metastable states in cellular automata for traffic flow[J].Eur Phys J，1998，5（3）：793-800.

[7]Hu S X，Gao K，Wang B H，et al.Cellular automaton model considering headway-distance effect[J].Chinese Physics B，2008，17（5）：1863-1868.

[8]Li X B，Wu Q S，Jiang R.Cellular automaton model considering the velocity effect of a car on the successive car[J]. Phys Rev E，2001，64（6）.

[9]薛郁，董力耘，袁以武，等.考虑车辆相对运动速度的交通流演化过程的数值模拟[J].物理学报，2002，51（3）：492-496.

[10]花伟，林柏梁.考虑行车状态的一维元胞自动机交通流模型[J].物理学报，2005，54（6）：2595-2599.

[11]薛郁，董力耘，戴世强.一种改进的一维元胞自动机交通流模型及减速概率的影响[J].物理学报，2001，50（3）：445-449.

[12]牟勇飚，钟诚文.基于安全驾驶的元胞自动机交通流模型[J].物理学报，2005，54（12）：5597-5601.

[13]邝华，孔令江，刘慕仁.多速混合车辆单车道元胞自动机交通流模型的研究[J].物理学报，2004，53（9）：2894-2898.

[14]雷丽，薛郁，戴世强.交通流的一维元胞自动机敏感驾驶模型[J].物理学报，2003，52（9）：2121-2126.

[15]陈时东，朱留华，孔令江，等.优先随机慢化及预测间距对交通流的影响[J].物理学报，2007，56（5）：2517-2522.

[16]彭莉娟，康瑞.考虑驾驶员特性的一维元胞自动机交通流模型[J].物理学报，2009，58（2）：830-835.

[17]丁建勋，黄海军，唐铁桥.一种考虑速度随机慢化概率动态演化的交通流元胞自动机模型[J].物理学报，2009，58（11）：7591-7594.

[18]Li F，Gao Z Y，Jia B.Traffic behavior in the on-ramp system with signal controlling[J].Physica A，2007，385：333-342.

[19]梅超群，黄海军，唐铁桥.高速公路入匝控制的一个元胞自动机模型[J].物理学报，2008，57（8）：4786-4793.

[20]藤亚帆，高自友，贾斌，等.信号灯控制下的主道双车道入匝道系统交通流特性研究[J].物理学报，2008，57（3）：1365-1374.

[21]雷丽，董力耘，葛红霞.基于元胞自动机模型的上匝道合流处交替通行控制的研究[J].物理学报，2007，56（12）：6874-6880.

[22]贾斌，高自友，李克平，等.基于元胞自动机的交通系统建模与模拟[M].北京：科学出版社，2007.

ZHU Changsheng1,MAYuting1,WANG Qingrong2，3

1.School of Computer and Communication,Lanzhou University of Technology,Lanzhou 730050,China
2.School of Electrical Engineering and Information Engineering,Lanzhou University of Technology,Lanzhou 730050,China
3.School of Electronic and Information,Lanzhou Jiaotong University,Lanzhou 730070,China

Based on the cellular automaton traffic model of on-ramp system,considering the behavior of changing lane form point of safe distance,a new traffic model is built.With the new model,the traffic flow is numerical simulated and investigated, and then some results are obtained.The lane-changing behavior has a huge effect on the flow of ramp model.The behavior without considering safe-distance can make the flow of ramp section to reach the highest point,while the flow of upstream and downstream sections of main road can be obviously suppressed.The lane-changing behavior considering both safe-distance of front and back can make the flow of upstream and down stream section of main road to get the highest point,and the flow of the whole system can reach the highest value.

on-ramp system;NaSch cellular automaton;lane-changing rule;safe distance

基于入匝道系统的元胞自动机交通流模型，从安全距离的角度提出四种换道规则，探讨四种换道规则对匝道系统的影响。模拟计算结果表明，匝道上的不同换道行为对匝道交通流模型有重大影响。安全距离为零的换道行为，能使匝道路段的流量获得最大值，但是却会抑制主道上游路段和下游路段的车辆流量；同时考虑了与前后车有安全距离的换道行为，不仅能让主道上下游路段的流量达到最大值，还能使整个匝道系统的流量达到最大值。

入匝道系统；NaSch元胞自动机模型；换道规则；安全距离

A

TP391.9

10.3778/j.issn.1002-8331.1111-0156

ZHU Changsheng,MA Yuting,WANG Qingrong.Research of vehicle’s lane-changing rules of on-ramp system with cellular automaton model.Computer Engineering and Applications,2013,49（13）：248-252.

兰州市科技创新人才团队计划项目（No.2010-2-3）；兰州理工大学红柳青年教师培养计划（No.Q200905）。

朱昶胜（1974—），男，博士，教授，研究方向：智能交通系统；马玉婷（1988—），女，硕士生，研究方向：智能交通系统；王庆荣（1977—），女，博士生，讲师，研究方向：智能交通系统。E-mail：myt6391709@163.com

2011-11-15

2012-03-06

1002-8331（2013）13-0248-05