BDE-LSSVM在柴油机气门故障诊断中的应用

曹龙汉，唐超，何俊强，武明亮，田力，吴珍毅

1.重庆通信学院 控制工程重点实验室，重庆 400035

2.重庆理工大学 汽车零部件制造及检测技术教育部重点实验室，重庆 400050

BDE-LSSVM在柴油机气门故障诊断中的应用

曹龙汉1，2，唐超1，何俊强1，武明亮1，田力1，吴珍毅1

1.重庆通信学院 控制工程重点实验室，重庆 400035

2.重庆理工大学 汽车零部件制造及检测技术教育部重点实验室，重庆 400050

1 引言

随着科学技术的飞速发展，机械设备朝着复杂化、综合化等高度自动化方向发展，从而造成机械设备结构日益复杂。柴油机是目前应用最广泛的动力设备之一，其自身结构十分复杂，因此柴油机故障必然呈现出复杂性和多样性的特点[1]。气门是柴油机中最容易发生故障的零件之一，其一旦发生故障将最终影响整台设备的性能，造成巨大的经济损失和人员伤亡。传统的定期检修和事后维修的成本高，效率低且缺乏事故预见能力[2]。预报潜在的故障并采取措施，不仅能够避免设备故障，而且能够节省维修费用，因此对柴油机气门故障的研究具有重要的现实意义。

人工智能技术的兴起使柴油机气门故障诊断研究实现了飞跃式的发展。近年来，一些人工智能算法被应用到故障诊断研究中，并取得了很好的效果，比如，模糊控制、人工神经网络、支持向量机等[3-5]。支持向量机通过结构风险最小化原理较好地解决了小样本、非线性等问题。最小二乘支持向量机（LSSVM）是支持向量机的一个改进，它采用平方项优化指标，并用等式约束代替支持向量机的不等式约束。LSSVM降低了计算的复杂程度，减少了求解时间，但模型的核函数参数的适当选择对模型的实用性影响很大。本文针对柴油机气门故障诊断小样本和非线性数据等问题，分析了改进的微分进化算法和支持向量机算法的优缺点，将其有机结合，建立了基于BDE的LSSVM故障诊断模型。

2 LSSVM多分类算法

最小二乘支持向量机将传统支持向量机中的不等式约束条件改为等式约束条件，以误差的二范数来表示，提高了传统SVM算法的收敛速度。

假定一个训练数据集(xi，yi)，i=1，2，…，l,xi∈Rn，yi∈R，则线性拟合函数如式（1）所示：

其中，w=(w1，w2，…，wn)为权值系数，b为阀值，φ(x)是把非线性问题转化成线性问题的维数变换函数[6]。

根据风险最小化原则，风险函数如式（2）所示：

约束条件如式（3）所示：

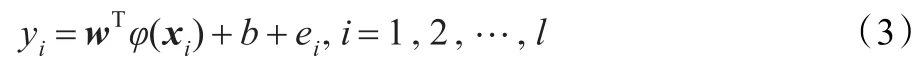
其中，c为惩罚因子，e为松弛因子。

通过引入Lagrange函数，再根据KKT（Karush-Kuhn-Tucker）条件，整理得式（4）：

式中，e1=[1,1,…,1]T，y=[y1,y2,…,yl]T，α=[α1，α2，…,αl]T，Q=φi(x)φj(x)=K(xi，xj)，(i，j=1，2，…，l)，其中K(xi，xj)为核函数。核函数的选择不存在性能的差异，由于径向基核函数计算相对简单，只有一个参数σ，所以采用式（5）形式核函数：

最终可以得到最小二乘支持向量机的最优分类函数，如式（6）所示：

3 基于BDE的LSSVM算法支持向量机参数寻优

利用BDE算法对LSSVM进行参数优化，是在种群空间内进行进化，每进化一代就产生新的参数，利用新的参数训练分类器，同时计算相应的适应度，然后判断是否满继续优化。

在基于径向机核函数的LSSVM中，需要优化的参数是惩罚因子c和内核参数σ，其中惩罚因子确定特征空间中支持向量机的经验风险比例和置信范围，内核参数影响数据转换到高维空间中的复杂程度[7]。

微分进化算法是一种实数编码的基于种群进化的进化算法。该算法通过对当前种群进行变异、交叉和选择操作，产生新一代种群，并逐步使种群进化到包含或接近最优解的状态[8]。

但是微分进化算法是基于编码的寻优算法，实用范围受到了很大的限制，对于特征选择分类问题，需要解决离散优化问题。文献[9]提出需要将差分进化算法进行二进制编码，本文提出了二进制编码的微分进化算法。

将二进制微分进化算法用于寻找最优特征，实质是选取最优二进制的向量。个体向量长度和样本也总数相等，每一位对应一个特征，为“1”则选取，相反为“0”就放弃，通过特征向量计算算法评价函数，再通过算法评价函数引导二进制微分进化算法进化方向，直至特征向量为最优。其具体步骤如下：

步骤1初始化种群规模N、进化代数km、交叉概率CR、缩放因子a、终止阀值、惩罚因子c和内核参数σ的门限值。

步骤2利用当前得到的(c，δ)作为LSSVM的参数，利用参数对样本数据进行训练并得到适应度函数值。

步骤3根据步骤2得到的适应度函数值与期望值进行对比，如果满足停止条件就跳转至步骤9；否则就进行下一步。

步骤4k=k+1，进入下一代进化。

步骤5从当前k代种群中随机选取3个与当前不同的个体，按照式（1）进行变异操作，产生新的变异个体yi。

步骤6接着按照式（3）对变异个体yi进行交叉操作，产生新的个体zi，j。

步骤7按照式（4）对k+1代实验个体zi，j进行选择操作，生成新的。

步骤8在k+1代种群中，计算产生新的(c，δ)，然后跳转至步骤2。

步骤9保存LSSVM的最优参数(c，δ)，停止寻优；针对本文提出了两种停止条件：进化代数k超过设定值时停止或者连续迭代设定次后适应度函数值小于给定值。

在BDE的参数寻优过程中，得到了最优核参数，把具体参数设置为LSSVM的核参数，并对数据进行分类训练，将训练好的模型再应用到诊断当中。

4 在柴油机气门故障诊断中的应用与研究

4.1 故障诊断流程

本实验是在型号为6135D柴油机上进行研究的，采用缸盖振动信号作为诊断信号，其原因因为振动信号可以反映出大量故障信息，并且振动信号易于信号处理和特征提取。故障诊断流程图，如图1所示。

图1 故障诊断流程图

实验步骤主要分四部分：

（1）测取缸盖振动信号。利用缸盖上的加速度传感器测取振动信号，不同故障对振动影响不一。

（2）特征提取与选择。将提取的振动时域信号经小波变换得到特征向量组，然后经过特征选择简化特征向量，最终形成数据样本。

（3）训练BDE-LSSVM模型。用优化算法优化诊断模型，将适应度函数值与给定值比较，最终得到最优参数，建立BDE-LSSVM故障诊断模型。

（4）故障诊断。用训练好的模型对测试样本进行诊断，同时验证诊断模型的效果。

4.2 采用小波变换的故障特征提取

型号为6135D柴油机为6缸机，点火顺序1-5-3-6-2-4，加速度传感器被安装在第一缸缸盖上，采样频率25 KHz，采样起始点以第一缸换气上止点为基准，柴油机空转一个工作周期为80 ms[2]。故障被分为气门间隙正常，排气门间隙小，排气门间隙大，轻微漏气以及严重漏气5类[10]，如图2所示，从上至下依次为这5种故障的时域图。

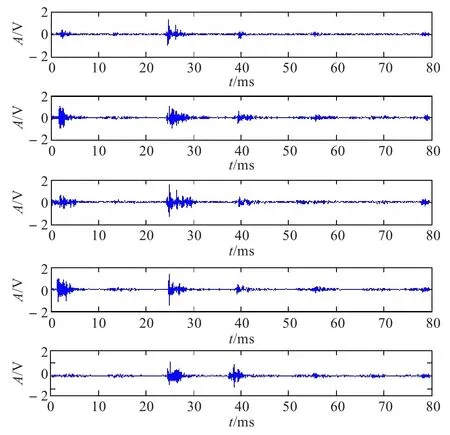
图2 气门在不同状态的时域图

将被测取数据经dB5小波包变换得到特征向量[11]，本文选取了25组气门故障特征向量，如表1，故障类型一列的1，2，3，4，5依次代表气门间隙正常，排气门间隙小，排气门间隙大，轻微漏气以及严重漏气5种状态，能量谱为5维。

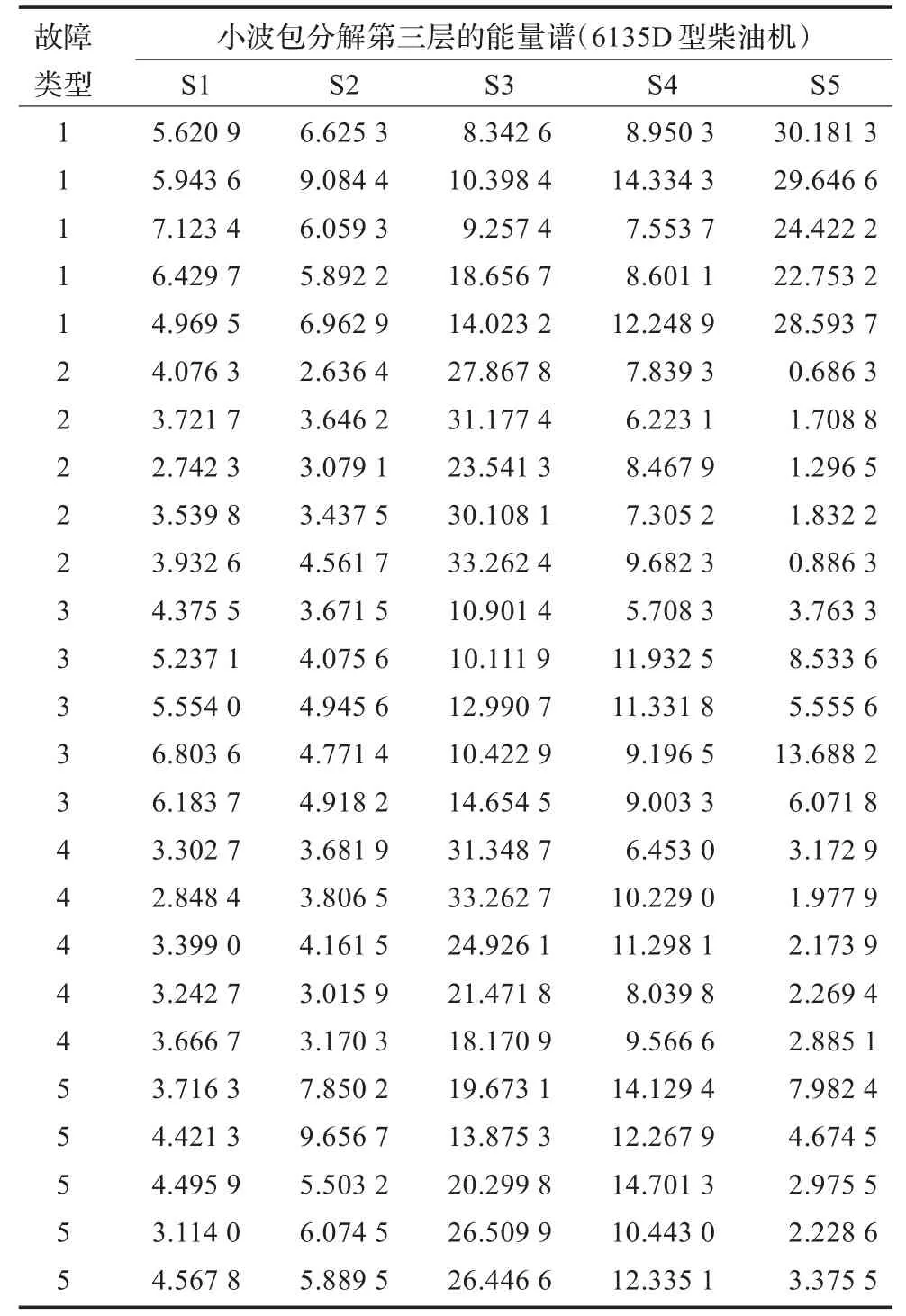
表1 气门故障样本

5 仿真结果分析

为了验证BDE-LSSVM模型的故障诊断能力，将其与文献[12]的遗传（GA）优化的LSSVM模型和文献[13]的粒子群（PSO）优化的LSSVM模型，在柴油机气门故障诊断中的性能进行比较。GA-LSSVM模型中，设定群体规模为20，交叉概率为0.4，变异概率为0.01，最大终止代数为500；PSO-LSSVM模型中，设定群体规模为20，惯性权重为1，加速因子C1=C2=2，最大终止代数为500；对于BDE-LSSVM，设定群体规模为20，变异概率为0.5，杂交因子0.6，最大终止代数500。经过BDE处理后的数据为5个故障特征，能量谱为5维，其中各故障特征前4组为训练样本，最后1组为测试样本，用训练好的LSSVM分类器对测试样本进行测试。三种算法的收敛曲线，如图3、图4和图5所示；三种算法的诊断结果与训练时间的对比，如表2所示。

图3 GA-LSSVM算法收敛曲线图

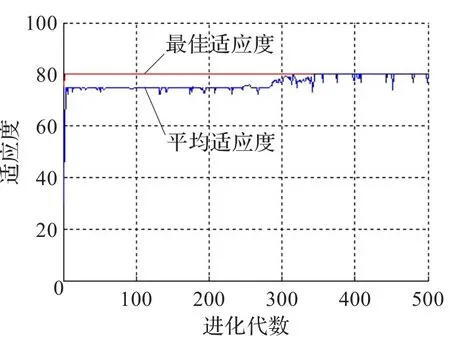
图4 PSO-LSSVM算法收敛曲线图

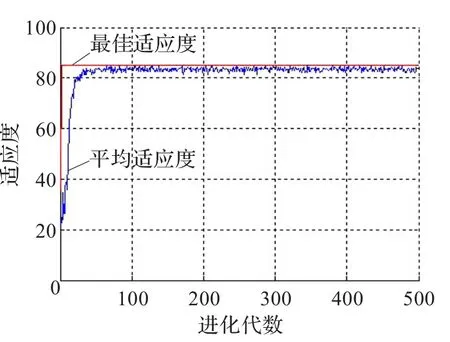
图5 本文BDE-LSSVM算法收敛曲线图

表2 三种算法诊断结果与训练时间对比

从图3、图4和图5可以看出，在三种算法的最佳适应度曲线中，BDE-LSSVM速度很快而且得到了很好的最佳适应度值；GA-LSSVM能得到较好的最佳适应度值但速度较慢；PSO-LSSVM速度很快但最佳适应度值最差。而从三种算法的平均适应度来看，BDE-LSSVM能较快得到很好的平均适应度值，相对稳定性也是最好；PSO-LSSVM得到的平均适应度值较好，相对稳定性较好但速度最慢；GA-LSSVM得到的平均适应度值较好，但速度较慢，稳定性最差。从表2可以看到，BDE-LSSVM算法的训练时间最短，且诊断正确率高达91.0%。

6 结论

柴油机气门故障诊断的实质是样本少和非线性数据特征的分类问题，LSSVM算法针对此类问题具有很好的效果，但参数选择影响着其性能的发挥。本文提出了一种BDE优化LSSVM的模型，利用BDE的全局收敛性和强鲁棒性优点对参数进行选取，实现了LSSVM参数的自动最优选择，并与GA-LSSVM和PSO-LSSVM模型在柴油机气门故障诊断方面进行比较。对比结果表明，BDE优化LSSVM的方法是可行的，它既克服了常规优化算法寻优效率较低的问题，而且提高了故障诊断的准确率。

[1]衣文凤.基于瞬时转速法分析柴油机各缸工作均匀性的数据处理和故障诊断[D].济南：山东大学，2009.

[2]曹龙汉.柴油机智能化故障诊断技术[M].北京：国防工业出版社，2005.

[3]刘冠军，苏永定，潘才华.基于综合型模糊支持向量机的故障诊断方法及应用[J].仪器仪表学报，2009，30（7）：1363-1367.

[4]张俊彩，钱旭，周玉.可拓神经网络在变压器故障诊断中的应用[J].计算机工程与应用，2011，47（7）：8-11.

[5]戴贤江，桂卫华，蒋少华.基于RS与LS-SVM的密闭鼓风炉故障诊断[J].计算机工程与应用，2008，44（10）：221-223.

[6]Suykens J A K，Gestel T V，Brabanter J D，et al.Least squares support vector machines[M].Singapore：World Scientific，2002.

[7]杨洁，郑宁，刘董，等.基于遗传算法的SVM带权特征和模型参数优化[J].计算机仿真，2008，25（9）：115-117.

[8]Bergey P K，Ragsdale C.Modified differential evolution：a greedy random strategy for genetic recombination[J].The International Journal of Management Science，2005，33：255-265.

[9]韩林，贺兴时.基于人工免疫系统的二进制差分进化算法[J].哈尔滨工程大学学报，2006，27（B07）：278-282.

[10]梅卫江，王春林，边金英.柴油机气门间隙异常故障振动诊断的实验研究[J].机床与液压，2010，38（17）：130-132.

[11]杨青，田枫，王大志，等.基于提升小波和递推LSSVM的实时故障诊断方法[J].仪器仪表学报，2011，32（3）：596-602.

[12]张大为，段哲民，李鹏，等.遗传优化的LSSVM在故障诊断中的仿真研究[J].计算机仿真，2010，27（10）.

[13]李玉军，汤晓君，刘君华.基于粒子群优化的最小二乘支持向量机在混合气体定量分析中的应用[J].光谱学与光谱分析，2010，30（3）：774-778.

CAO Longhan1，2,TANG Chao1,HE Junqiang1,WU Mingliang1,TIAN Li1,WU Zhenyi1

1.Key Laboratory of Control Engineering,College of Chongqing Communication,Chongqing 400035,China
2.Key Laboratory of Manufacture and Test Techniques for Automobile Parts,Ministry of Education,Chongqing University of Technology,Chongqing 400050,China

Aiming at problem of few samples and non-linear characteristics in diesel engine fault diagnosis,Least Squares Support Vector Machine（LSSVM）can be better to diagnostic studies,but the results of diagnosis are greatly influenced by the penalty factor and the selection of kernel parameters,it is necessary to optimize its parameters,LSSVM algorithm based on Binary Differential Evolution（BDE）is proposed.For the data of diesel engine valve vibration signal used as the characteristics values of model,and wavelet transformed,the fault diagnosis model based on BDE-LSSVM is established.Compared with LSSVM model based on the particle swarm algorithm and genetic algorithm,the results show that LSSVM with BDE has better fitness value and stability,as well as more perfect accuracy and speed in the diagnosis classification.

Least Squares Support Vector Machines（LSSVM）;Binary Differential Evolution（BDE）;fault diagnosis;wavelet transform

针对柴油机气门故障的诊断样本少和非线性数据特征等问题，最小二乘法的支持向量机（LSSVM）能够较好地进行诊断研究，但由于惩罚因子C和内核参数σ的选取对诊断结果影响较大，有必要对其进行参数优化，因此提出了基于二进制微分进化算法（BDE）的最小二乘法支持向量机算法。利用柴油机气门振动信号作为数据，经小波变换作为模型特征，建立了基于BDE-LSSVM故障诊断模型，并与基于遗传和基于粒子群算法的LSSVM模型进行柴油机气门故障诊断的性能对比。比较结果证明，基于BDE优化的LSSVM模型在故障特征选取前后具有更好的适应度值和稳定度，故障分类准确性高且运算速度更快。

最小二乘支持向量机；二进制微分进化；故障诊断；小波变换

A

TP206

10.3778/j.issn.1002-8331.1111-0031

CAO Longhan,TANG Chao,HE Junqiang,et al.Application of BDE-LSSVM in diesel engine fault diagnosis.Computer Engineering and Applications,2013,49（13）：241-244.

国家科技部国际科技合作项目（No.2007DFR10420）；重庆理工大学汽车零部件制造及检测技术教育部重点实验室开放基金（No.2009-10）。

曹龙汉（1966—），男，博士，教授，主要研究方向为故障诊断与智能控制等。

2011-11-07

2012-01-11

1002-8331（2013）13-0241-04

CNKI出版日期：2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1723.095.html