遗传算法在多品种小批量模式MPS中的应用

杨美荣，崔曼曼，史建锋，肖玲诺

1.哈尔滨工业大学 经济管理学院（威海），山东 威海 264209

2.哈尔滨工业大学 管理学院，哈尔滨 150001

3.哈尔滨工业大学 人文与社会科学学院，哈尔滨 150001

遗传算法在多品种小批量模式MPS中的应用

杨美荣1，崔曼曼2，史建锋2，肖玲诺3

1.哈尔滨工业大学 经济管理学院（威海），山东 威海 264209

2.哈尔滨工业大学 管理学院，哈尔滨 150001

3.哈尔滨工业大学 人文与社会科学学院，哈尔滨 150001

1 引言

传统大规模生产的优势在于能够通过规模经济降低成本，但是却不能灵活适应市场需求。随着市场需求的多样化和个性化，多品种小批量生产己成为制造业的主要生产方式之一。这种生产方式能够灵活地适应市场多样化的需求，但由于产品种类多、批量小，工艺过程也不相同，产品生产计划的稳定性差，给企业生产管理带来诸多困难。在激烈的市场竞争中，如何在保证企业经济利益的同时，快速响应客户个性化需求，提高客户满意度是企业最关心的问题。在多品种小批量生产模式下，企业大多是根据客户订单组织生产的，因此拥有方便、快捷、有效的主生产计划（Master Production Schedule，MPS）是快速有效解决客户需求的重要途径。客户订单的数量以及订单要求的品种数量较多，因此需要营销部门与生产部门共同对订单进行评估，决定是否可以接单。MPS根据客户订单和企业生产能力，把经营计划或生产大纲中的产品系列具体化，使之成为展开物料需求计划的主要依据，起到了从综合计划向具体计划过渡的承上启下的作用。

MPS的编制和优化问题一直受到学术界重视。从国外研究来看，生产计划模型大多是线性规划模型或者是整数规划模型，其中线性规划模型使用最多。Chu[1]从整体的综合生产计划问题到最基本的产品装配问题，针对不同层次模型的复杂性，用线性规划方法给出了详细的解决方案；Byrne和Bakir[2]等采用分析/仿真混合的方法求解生产计划问题，得到很好的效果。主生产计划理论与排单问题是分不开的，解决这个问题的关键在于排单算法。对此，国外已经进行了很多年的研究，发展出几十种先进生产排程算法，比较常用的如：专家系统、模拟退火法、神经网络优化等，这些算法各有优劣，可用在不同场合。目前新的不同算法仍正在蓬勃发展中。在系统开发上，比较有影响力的ERP软件商有德国的SAP，美国的Oracle和SSA，以及瑞典的IFS等几家。

国内，许多研究人员对主生产计划模型建立这一课题也进行了研究。徐福缘等人[3]用线性目标规划方法构造了一个多品种小批量生产条件下的企业年度生产计划模型，通过设备工时约束，使关键设备加工台时不超过全年提供的台时；王时龙[4]等人利用知识工程的原理解决了多品种小批量模式下成批成套生产问题。除此以外，越来越多的学者从不同的角度，采用不同的解决方法对主生产计划算法进行优化。于晓义[5]等针对多协作车间的并行协同计划调度问题，提出了基于工序约束的并行协同进化遗传算法。刘敏[6]针对遗传算法求解过程长，易走向局部最小值等特点，提出了自适应退火遗传算法，解决了车间日作业计划的调度问题。但由于多品种、小批量条件下的作业是一个NPC问题，至今世界上还没有一个效率高且通用的优化算法。国内，MPS系统开发比较好的主要是用友、金碟、浪潮通软、神州数码等几家大型ERP软件开发商。但是由于排产技术瓶颈的存在，中国大多数企业目前仍然停留在对BOM低层次的完善和对进销存财务模块低水平重复开发上。其中，绝大多数的MPS系统只是编织一个初稿计划，然后计算能力需求情况，因而它只提供一个作为能力平衡的依据，大多情况下还是要依靠人来调整。

2 主生产计划排单模型

在理想生产条件下，比如人力、原材料等资源都充足，设备的能力问题就是决定企业产出的关键。根据约束理论（Theory of Constraints，TOC）和准时制生产（Just in Time，JIT）思想[7]可知设备能力是一个约束，而产品提前期是另外一个约束，解决问题的关键就是要最大限度地利用这两个约束保证瓶颈设备得到充分利用，保证产品提前期得到很好的满足。针对这个问题，本文建立一个以关键工作中心能力利用率最大化和提前/拖期罚款[8]最小为目标的数学模型。

2.1 能力约束模型

本文分析能力约束的条件是在理想的生产条件下，即物料、人力等资源充足。MPS制定的一个主要问题是充分合理地利用瓶颈资源，使关键工作中心的能力利用率最大。能力利用率的计算如公式（1）：

能力利用率=生产产品占用的能力/总能力＝

m表示涉及到m种关键工作中心；n表示企业需要生产n种规格的产品；k表示企业要对n种产品制定k个时段的主生产计划；Xijh表示i时段h设备上加工j产品的数量；qijh表示i时段h设备上加工j产品所需要占用的额定能力；Ujh表示i时段h设备的额定可用能力。

在实际生产中，生产产品占用的能力不能大于总能力，

此数学模型符合约束理论的思想，能直观表现出能力的利用率情况。本文研究的目标就是使关键工作中心的能力利用率最大化。

2.2 提前期约束模型

MPS制定中的另一个主要问题是确定订单的投产日期。关于提前期约束模型的建立，可以考虑企业拖期罚款和提前的成本。如果不能按交货期交货就是违约，要按照一定的比例向客户付违约费用。因此，拖期时间越短，拖期罚款越少，企业的利润越高。还要考虑过早完成订单生产增加的管理成本。本文提出基于JIT的惩罚函数，以拖期罚款和因提前生产而引起的库存保管费之和最少为目标来建立数学模型。模型中用到的提前期是指产品的生产提前期，生产提前期通常是变动的，提前时间的长短随着每批加工量大小而变动。惩罚函数计算如公式（2）：

其中Tj=T′j+lj×Xj。n、m、k定义同上，Xj为j产品本次投产的数量，Xij为i时段j产品的生产数量；Tj为第j种产品的提前期，Tj由固定部分（计划提前期）Tj'和可变部分构成，lj为单位产量增加的提前期；rj为第j种产品的投产日期，dj为第j种产品的合同交货日期；βj为单位时间（天）拖期惩罚因子；αj为单位时间（天）提前惩罚因子。

2.3 主生产计划排单的双目标数据模型

综合以上分析，建立主生产计划排单的双目标数学模型如公式（3）、（4）：

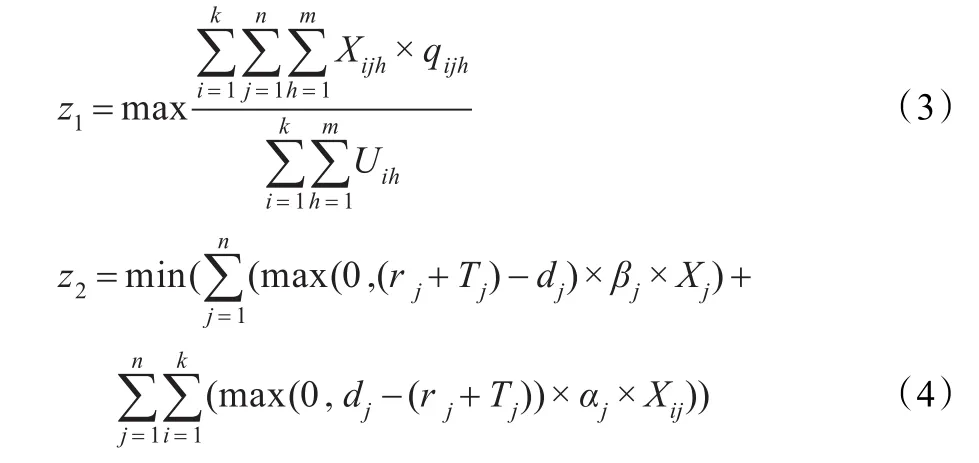
其中，z1表示设备的能力利用率最大，z2表示惩罚金额最小。对两个公式分析后发现，z1求最大比率，z2求最小数值，计算求解时很不方便。对模型进行以下转换：对z1求倒数，z2转化为求罚款和订单金额比值，其思想与z2模型的思想一致。转换后的数学模型如公式（5）、（6）：

Cj为j产品本次投产的订单金额，y1表示设备能力利用率的倒数，y2表示罚款与订单金额比值的最小值。

3 基于遗传算法的MPS模型优化设计

3.1 遗传算法思想

遗传算法（Genetic Algorithm，GA）首先采用某种编码方式将解空间映射到编码空间，每个编码对应问题的一个解，称为个体或染色体，再随机产生一群初始个体，称为种群，种群中的每个染色体是问题的一个解。染色体的好坏用适应度来衡量。在后续迭代中，按照适者生存原理，根据适应度大小挑选染色体，并借助各种遗传算子对染色体进行交叉和变异，交叉或变异运算后生成下一代染色体，称为后代。根据适应度的大小从上一代和后代中选择一定数量的染色体，作为下一代群体，再继续进化。经过若干代之后，算法收敛于最好的染色体，它很可能就是问题的最优解或次优解。

GA包括三个基本操作[9-10]：选择、交叉和变异。选择操作实现对群体中的染色体的优胜劣汰，适应度高的个体被遗传到下一代群体中的概率大，反之概率小。常用方法有：轮盘赌法、排序法、随机联赛选择法、最佳个体保留法；交叉运算是指对两个相互配对的染色体按某种方式相互交换其部分基因，从而形成两个新的个体，目前常用的配对策略是随机配对。交叉算子的设计包括两方面的内容：一是如何确定交叉点的位置，二是如何进行部分基因的交换；常用的交叉算法有：单点交叉、双点交叉、均匀交叉、算术交叉。变异运算指将个体编码串中的某些基因值用其他基因值来替换，从而形成一个新的个体。遗传算法中的变异运算决定了遗传算法的局部搜索能力。交叉运算和变异运算相互配合共同完成对搜索空间的全局搜索和局部搜索，常用的变异算法有：基本位变异、均匀变异。

遗传算法（GA）的步骤如图1所示。

3.2 基于GA的MPS模型的优化设计

3.2.1 染色体的编码设计

GA的优化过程不能直接作用在问题空间的参数，必须把它们转换成遗传空间中由基因按一定结构组成的染色体，这一转换操作称为编码，编码的选择是影响算法性能与效率的重要因素。常用的遗传编码方式有二进制编码、实数编码、字符编码[11]等。

图1 遗传算法逻辑流程

显然这样的一条染色体就是问题的一个解；而且这种实数编码方法无需解码，计算结果可直接作为主生产计划的方案。

3.2.2 种群初始化

首先对一个染色体的基因串，使用Random（0，Xj）（j= 1，2，…，n）方法随机生成一组基因串，即某个时段生产的各种产品的数量（在0和Xj之间的一个数值），如Xij，然后计算（Xj－Xij），再利用Random（0，Xj－Xij）随机生成染色体的下一组基因串。用此种方法生成一个染色体的基因串。值得注意的是，最后一个时段基因串的产生方式：

由于每个个体的基因串的产生是随机的，个体的多样性可得到保证。用上述方法产生的个体能够自动满足约束条件，大大减少了产生初始可行解的计算量。种群中所有个体的基因串都用此种方式产生，直到产生规定群体数目。

本文研究的问题的种群数目Num的选取与订单的个数及计划期的时段数有关，Num的取值大小会影响搜索的收敛速度。当下达的订单个数较多时，Num取值应较大；否则，Num取值较小。根据多次实验结果分析，当订单小于8时，Num取200；否则，Num取400。

3.2.3 适应度函数的确定

适应度函数是适应度与问题参数之间的函数关系。本文研究的目标就是使f（x）=y1+wy2达到最小，其中，w为目标y2在总目标中所占权重，其值根据企业的喜好偏重而定。在本文分析中，取w=0.6。把f（x）转化为最大值形式后作为算法中的适应度函数，即G(x)=C-f(x)。其中C为事先给定的足够大的常数。分析可知y1≤1，y2＜1，所以可取C=100。

3.2.4 选择

本文选用了这样一种方法进行选择：首先将每代中最优的一个染色体直接复制到下一代，然后对其他染色体采用轮盘赌方式按其适应度进行选择，如此重复，直到满足种群个体数。这种选择算法可保证迄今为止所得到的最优个体不被淘汰，它是GA收敛的一个重要保证条件。而且遵循优胜劣汰的规律，适应度大的染色体被选中的概率大。

3.2.5 交叉

交叉率的选择决定了交叉操作的频率，频率越高，可以越快地收敛到最有希望的最优解区域，因此一般选取较大的交叉率，但太高的频率也可能导致过早收敛，基本GA中交叉率一般取0.4～0.9。根据多次实验结果分析，交叉率取0.8。

3.2.6 变异

根据个体的变异率，对经过交叉操作的群体中的个体进行变异操作。这里采用在染色体中随机选择父代个体矩阵的两行进行互换，产生新的个体矩阵。这种操作方式使得除订单的交货期顺序有变化之外其他约束条件没有被破坏。与交叉算法一样，变异算法在随机选择配对染色体时选用除第一个个体以外的其他个体，这样可保证迄今为止所得到的最优个体不受变异操作的影响保留至下一代，避免种群退化。

变异率的选取受种群大小、染色体长度等因素影响，在基本GA中，变异率通常选取很小的值，一般取0.001～0.1。若选取高的变异率，虽然增加样本模式的多样性，但可能会引起不稳定。种群大小及染色体长度越大，变异率选取越小。根据多次实验结果分析，变异率取0.1。

3.2.7 终止条件

终止条件也是GA中的一个重要方面，因其直接关系到算法的效率。一般情况下若给定满足的条件，则直接用其作为终止条件或给定遗传代数作为终止条件。本文采用直接给定其遗传代数作为其终止条件。

4 算法应用结果分析

利用前面建立的主生产计划排单模型及GA对模型的优化设计，采用面向对象的编程语言Java实现了该算法。将企业生产中的具体数据通过上述算法仿真运算，对计算结果进行分析，证实该算法在一定程度上提高了适应度值，即对解决此问题具有一定效果。具体数据如下：

假设企业要对5份订单的10个订单项目进行主生产计划安排。物料主文件如表1所示，订单项目信息如表2所示，按交货时间排序后的订单项目信息如表3所示。主生产计划的计划展望期从2008年7月15日开始，至2008年8月11日结束；时段以周为单位，即时段的时间跨度为7天，共有4个时段。

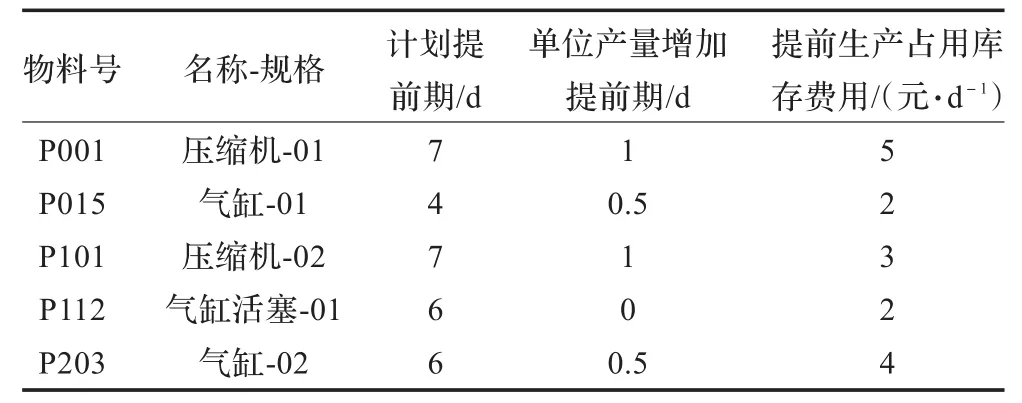
表1 物料主文件

表2 订单项目信息

表3 按时间排序后的订单项目信息

GA中交叉率、变异率、群体规模、遗传代数等各参数的选取对算法收敛的速度和结果都有影响。本文对GA各参数经过多次运算分析，交叉率取0.8，变异率取0.1，遗传代数取100，取群体规模为400。用GA对MPS模型进行优化求解，求得结果如表4；仅按交货期随机生成的MPS如表5。

表4 经过GA生成的MPS1）

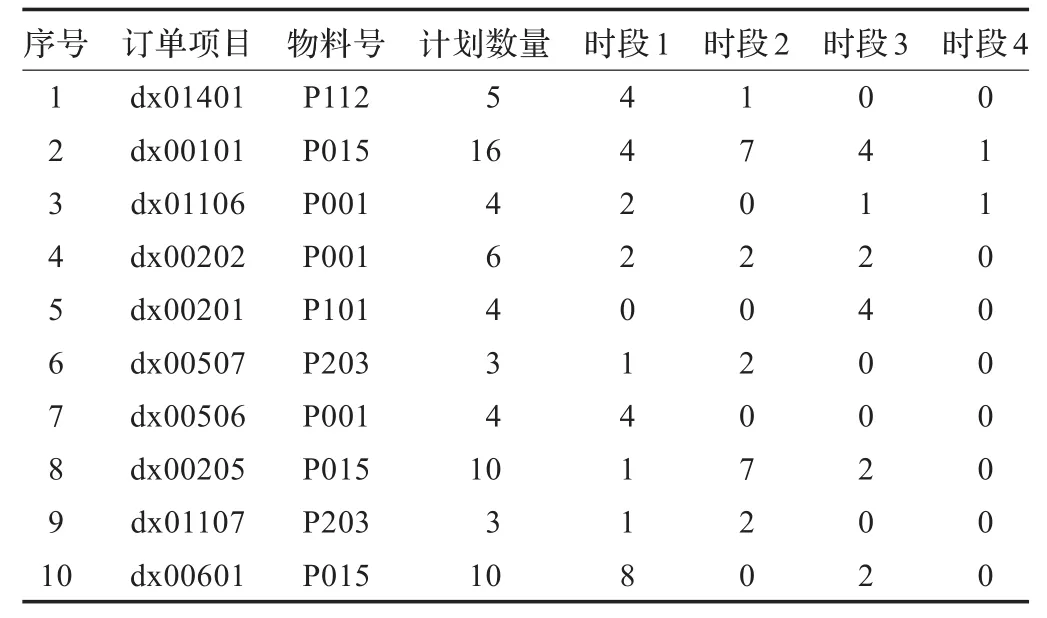
表5 仅按交货期随机生成的MPS

对表4与表5结果进行分析：用GA进行优化计算得出的主生产计划方案适应度为G（x）=98.91，目标函数的结果为f（x）=1.09；仅利用交货期的顺序随机生成的主生产计划得出的适应度为G（x）=98.77，目标函数是f（x）=1.23。由此可知GA优化结果更好。把表4及表5结果分别带入数学模型进行验证，发现表4罚款金额较小（454元＜1 596元），关键工作中心利用率较高（0.93＞0.86），证实优化结果基本符合生产的实际要求。因此，用GA解决此问题是正确有效的。

5 结束语

本文详细介绍了MPS双目标排单模型的建立，然后提出了MPS排单模型的GA优化设计与实现的具体方法和步骤，最后给出了排单模型GA优化的实例分析，证明了GA的可行性。该算法在某些时候可能会收敛于局部最优解，此时增加遗传代数可以在一定程度上避免这个问题。

[1]Chu S C K.A mathematical programming approach towards optimized master production scheduling[J].International Journal of Production Economics，1995，38：269-279.

[2]Byrne M D，Bakir M A.Production planning using a hybrid simulation analytical approach[J].International Journal of Production Economics，1999，59：305-311.

[3]徐福缘，凌佩雯，范晋鹰.一个小批量多品种的生产计划模型[J].工业工程，2000，4（3）：44-46.

[4]王时龙，易力力，任亨斌，等.多品种小批量成批成套生产滚动计划的生成方法[J].重庆大学学报，2009，32（9）：1024-1042.

[5]于晓义，孙树栋，褚崴.基于并行协同进化遗传算法的多协作车间计划调度[J].计算机集成制造系统，2008，14（5）：991-1000.

[6]刘敏，严隽薇.基于自适应退火遗传算法的车间日作业计划调度方法[J].计算机学报，2007，30（7）：1164-1172.

[7]李艳，吉卫喜.基于投产数量的实数编码遗传算法在双目标主生产计划模型中的应用[J].机械制造，2006，44（8）：62-64.

[8]Stevenson W J.Production operations management[M].张群，张杰，译.北京：机械工业出版社，2000：391-413.

[9]王小平，曹立明.遗传算法理论应用与软件实现[M].西安：西安交通大学出版社，2002：5-20.

[10]Hajela P，Lee E，Cho H.Genetic algorithms in topologic design of grillage structure[J].Computer-Aided Civil and Infrastructure Engineering，1998，13：13-22.

[11]石苓，窦延平.基于生产计划排单的遗传算法的优化与应用[J].计算机仿真，2005，22（4）：86-89.

YANG Meirong1,CUI Manman2,SHI Jianfeng2,XIAO Lingnuo3

1.School of Economics and Management at Weihai,Harbin Institute of Technology,Weihai,Shandong 264209,China
2.School of Management,Harbin Institute of Technology,Harbin 150001,China
3.School of Humanities and Social Science,Harbin Institute of Technology,Harbin 150001,China

According to Just-in-Time production and Theory of Constraints,centering on two restrictions of producing ability of key work center and production lead time,determining the maximum utilization of key work center and the least earliness/tardiness fine as the two goals of MPS model,this paper presents a double-goal MPS model based on multi-variety and small-batch enterprise. It uses GA to optimize the MPS model.Through analyzing the results of the enterprise data,GA has been proved to be effective.

master production schedule;Theory of Constraints（TOC）;Just-in-Time（JIT）;Genetic Algorithms（GA）

结合准时制生产和约束理论，以“关键设备产能”和“产品提前期”两大约束为重心，确定以关键工作中心利用率最高和提前/拖期罚款最少作为MPS模型的两个目标，提出了一种多品种、小批量生产模式下企业MPS的双目标排单模型的建立思路和方法；应用遗传算法对模型进行优化计算，通过对企业实例数据的运行结果分析，验证了方案的有效性。

主生产计划；约束理论；准时制生产；遗传算法

A

TP311

10.3778/j.issn.1002-8331.1110-0351

YANG Meirong,CUI Manman,SHI Jianfeng,et al.Applications of Genetic Algorithm in production planning of multi-categories and small batch mode.Computer Engineering and Applications,2013,49（13）：266-270.

山东省自然科学基金（No.2009ZRA10043）。

杨美荣（1980—），女，讲师，主要研究方向：ERP、J2EE系统架构与开发。E-mail：ymr324@163.com

2011-10-18

2012-01-06

1002-8331（2013）13-0266-05

CNKI出版日期：2012-03-21http://www.cnki.net/kcms/detail/11.2127.TP.20120321.1734.012.html