基于颜色特征的地板层次分类研究
钱勇,白瑞林,倪健,杜斌
江南大学 智能控制研究所 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
基于颜色特征的地板层次分类研究
钱勇,白瑞林,倪健,杜斌
江南大学 智能控制研究所 轻工过程先进控制教育部重点实验室,江苏 无锡 214122
1 引言
随着经济的快速发展,地板的需求量亦越来越大,地板在生产过程中如何快速准确地分类,成为了一个迫切需要解决的问题。目前,地板的分类实现主要靠人工目测,其人为因素的影响比较大,因此利用数字图像处理技术对地板进行分类,更能有效地保证地板分类的准确性。
由于地板颜色是反映地板表面视觉和心理感觉的重要特征,与分类的评定有着密切关系,从而使得近年对基于颜色特征的分类处理进行了一定的研究。如戴天虹等通过主颜色特征,分别利用神经网络中的RBF网络、K-最近相邻和最近邻对木材样本图像进行分类处理[1];王克奇等利用均匀色彩空间对木材的颜色特征进行测量与辨别[2];相似的还有竹片[3]及瓷砖[4]等材料基于颜色的的分类研究。
然而在上述的研究中,皆没能有效地去除光照条件及地板纹理特征对颜色分类效果的影响。本文通过在HSV色彩空间去除光照条件对其影响,并给予色调分量及饱和度分量不同的权重以减小纹理特征影响,对未知类别的地板样本进行分类处理。通过建立粗分类及细分类两层样本分类依据库,对未知地板样本最短距离决策、K-最近相邻对未知地板样本进行逐层分类处理,实现地板快速分类。
2 特征提取原理
2.1 HSV色彩空间
在颜色表示上,采用更加符合人眼对色彩感知的HSV色彩空间,以一个亮度的属性值V和两个色度属性值(色调H、饱和度S)来表示一种色彩。其中,RGB色彩空间转换HSV色彩空间的计算公式为:

2.2 颜色特征
对颜色特征的表达方法有直方图法、主色调法、颜色聚合矢量法、颜色矩法及颜色熵法等[5]。其中,颜色矩同其他颜色特征相比,无需对颜色进行量化处理,同时又降低了颜色特征的维数。其思想在于:图像中任何的颜色分布都可以用它的矩来表示,且颜色分布信息主要集中在低阶矩中[1,6],如一阶矩μ描述平均颜色,二阶矩σ描述颜色方差,三阶矩s描述颜色的偏移性。这种近似的方法能够十分有效地表征图像的颜色分布,从中可以看出颜色的差异(色差)。
颜色矩特征的三个低阶矩的数学表达式的形式为:
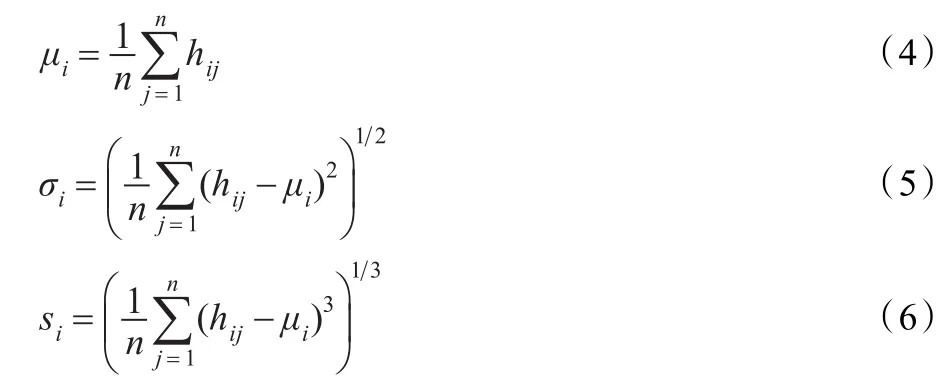
式中,hij表示第i颜色通道中灰度为j的像素出现的概率,n表示灰度级数。
为降低光照条件对地板分类效果的影响,在此选用两个色度属性值(色调、饱和度)提取其相关颜色矩特征以进行地板的分类检测处理,去除亮度的属性值。
通过观察地板样本的颜色特征数据发现,由于受到地板纹理特征的影响,地板样本饱和度特征数据分布离散性较高,使得饱和度特征数据不能有效地刻画出同类地板的颜色特性。但色调特征都保持着相对较好的集中性。因此在地板之间相似度的度量上需要给色调特征数据分配较高的权重,给饱和度特征数据分配较低的权重,以减小纹理特性对地板分类的影响。不同地板颜色矩向量的加权欧式距离可表示为:
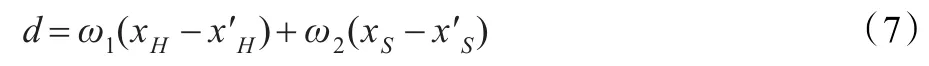
其中,ω1、ω2分别表示色调颜色矩特征及饱和度颜色矩特征的权值。
3 建立地板分类依据库
3.1 最大最小距离算法
聚类分析中一个重要的环节就是找到数据中客观存在的类别数目。当聚类中心数c未知时,有两种途径去处理:(1)尝试多种可能的c,并比较不同的准则函数值,选最优准则值所对应的c值进行聚类;(2)设置一个阈值来控制新的聚类类别的建立。
后一种方法对在线学习更为适合,其主要有最临近规则的试探法及最大最小距离算法[7],而最临近规则的试探法受到阈值T的影响很大。阈值的选取是分类成败的关键之一,而最大最小距离算法充分利用样本内部特性,计算出所有样本间的最大距离作为归类阈值的参考,改善了分类的准确性。若某样本到某一聚类中心的距离小于最大距离Dmax的1/2,则归入该类;否则建立新的聚类中心。
3.2 建立分类依据库过程
在地板分类实现之前预先建立给定地板样本分类依据库,以便对未知地板样本进行层次分类,实现未知地板样本快速有效的分类。其层次结构,如图1所示。
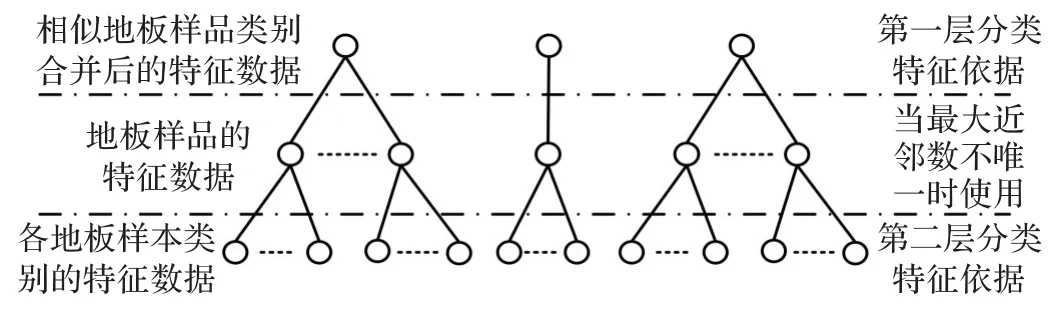
图1 样本分类依据库示意图
在建立样本分类依据库时,首先根据给定的地板样本确定出各地板样品的颜色矩,然后通过最大最小距离分类算法对各地板样品进行聚类处理,将颜色矩数值相近类别合并到一起,求取相似类别地板样品颜色矩的数据均值。
使用相似地板样品合并后的特征数据作为分类过程的初次分类的依据,用以确定未知地板样本的所属的近似类别。而预先给定的各地板样本颜色矩数据则作为第二次分类的依据,用以确定未知地板样本的所属的准确类别。
4 地板层次分类实现
4.1 分类决策方法
4.1.1 最短距离分类
最短距离分类规则[8]最初是由Cover和Hart于1967年提出的,其分类识别率可以用来比较不同特征矢量对样本描述的有效性。它的基本思想是:计算输入数据向量到表示所有目标类数据向量的距离,当到某一类的距离比到其他任何类的距离都短时,将未知模式分配到这一类[9]。
4.1.2 K-最近相邻分类
K-最近相邻是一种基于统计的分类方法,其基本思想是:从测试样本点x开始生长,不断地扩大区域,直到包含进k个训练样本为止,并且把测试样本点x的类别归为这最近的k个训练样本点中出现频率最大的类别[10]。
然而在实现时经常遇到的问题是:在x的k个近邻中,属于最大近邻数对应的类别可能不只一个。针对上述问题,将K-最近相邻法与最短距离法相结合,提出了K-最近相邻-最短距离法。其思路是:首先求出样本x的k个近邻。设最大近邻数为kmax,判断kmax是否唯一;若唯一,则该类别ωmax为x所属;若是多个(如N个),求近邻数kmax的所属地板样品类别特征均值与x的距离:

其中,S为地板样品类别特征均值,n为特征数目。
此时决策规则为:
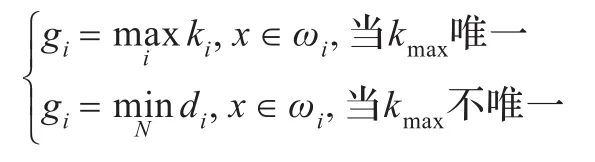
4.2 未知地板样本处理过程
在分类的实现过程中,首先通过最短距离分类判断未知地板样本所属的近似样品类别,然后通过K-最近相邻分类实现未知地板样本准确类别的判定实现,其具体实现流程如图2所示。
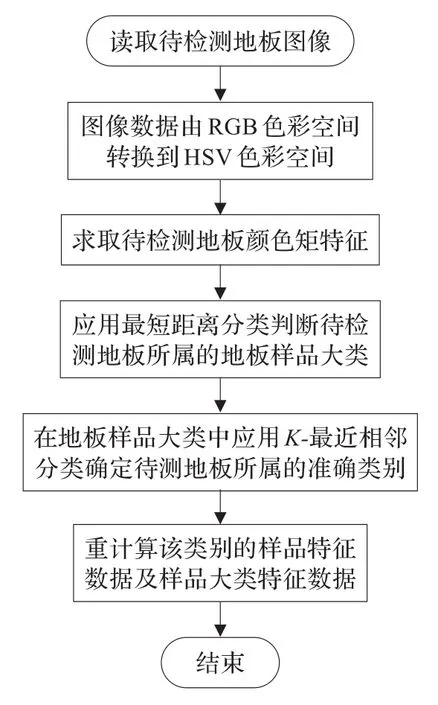
图2 未知地板样本分类实现流程图
在建立地板分类样本库时,由于初始类别中心选定的随机性,会使位于所有样本最大距离Dmax的1/2附近的同一样品的不同样本,在分类时判定到不同的近似类别,从而产生最终的分类错误。所以在判定样本类别时,定义一个中间区域。当未知样本进入此区域时,将与之相近的类别同样归入到下一层判定。
其具体实现步骤为:
(1)计算未知样本特征向量到所有相似类别合并后的向量的距离;
(2)对所有距离进行排序处理;
(3)将与最短距离之差小于Dmax/4的所有相似类别皆归算到下一层次的处理过程。
K-最近相邻分类确定待测地板所属准确类别的实现过程:
(1)求取未知地板样本与所属样品大类中各样本的距离;
(2)按距离大小对样品大类中各样本进行排序处理;
(3)统计前N个距离所对应的地板样品类别数目,求取类别数目最大值Kmax;
(4)判断Kmax是否唯一,唯一则进行第(5)步,不唯一则进行第(6)步;
(5)则将未知地板归类到Kmax所对应的类别中,分类处理结束;
(6)求取待测地板与所有Kmax相同的地板样品的距离;
(7)将未知地板样本归类到与其距离最小的地板样品中,分类处理结束。
5 结果与分析
在上位机以270个地板样本图像进行分类实验,共9类样品,每类各30个样本,其中15个地板样本用于建立分层依据库,剩下的15个地板样本用于未知地板样本分类检测;通过VS2010操作平台进行仿真。各类别地板样品的色调及饱和度颜色矩特征均值数据,如表1所示。
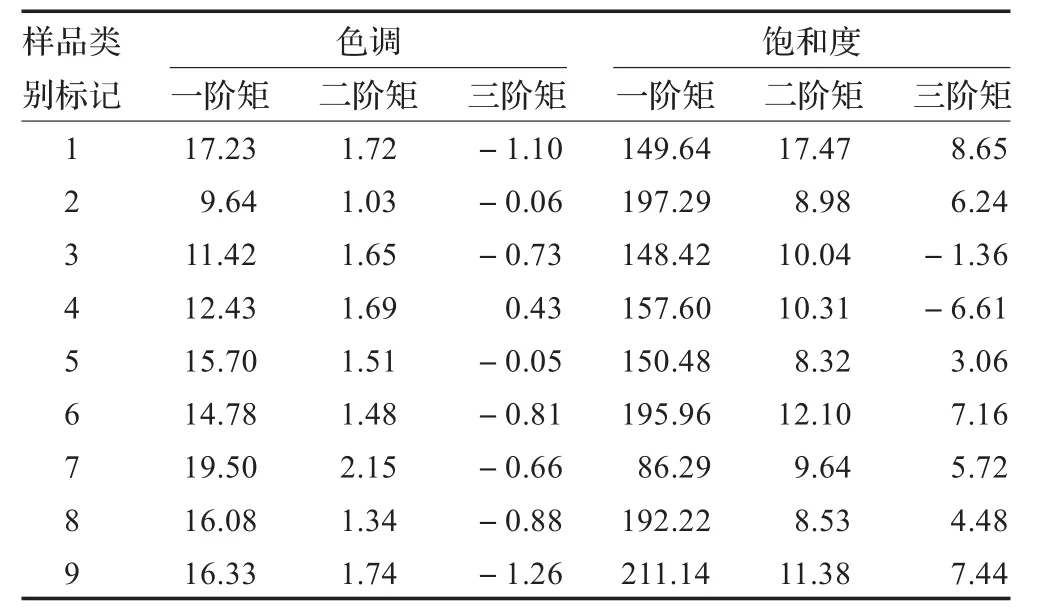
表1 样品色调及饱和度颜色矩特征均值
通过最大最小距离法对9种地板样品进行聚类处理后,求取的相似类别地板样品颜色矩特征的具体数据均值参数及其所包含的地板样品序号,如表2所示。
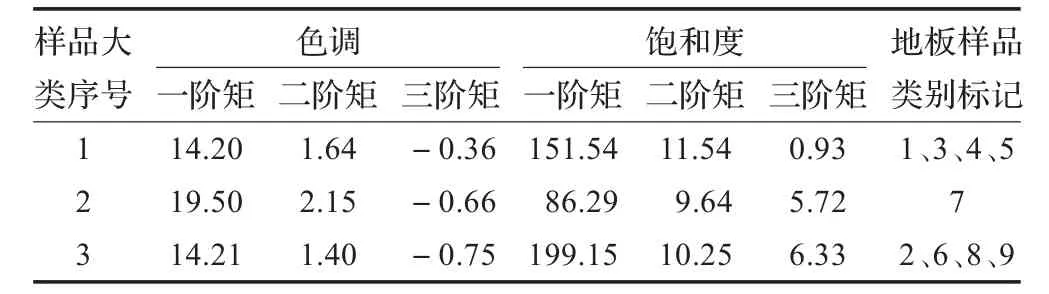
表2 相似类别地板样品相关参数
在本文分类方案下,不同饱和度权重所对应的正确率的对比关系,如图3所示。通过观察可以看出,在饱和度权重为10%时,其地板纹理对未知地板样本分类的影响最小,正确率最高,约为95.6%。
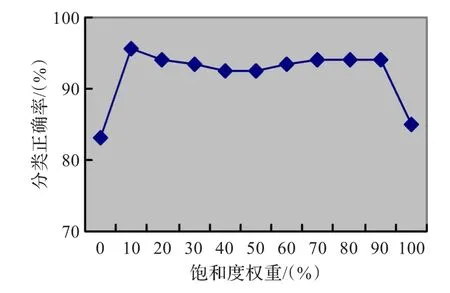
图3 饱和度权重与分类正确率对比关系
用本文方法与其他相关分类算法对135个地板样本进行分类,其正确率及单地板样本于上位机分类检测平均时间对比结果,如表3所示。通过观察可以看出,本文分类方案具有较高的正确率及较快的分类速度。
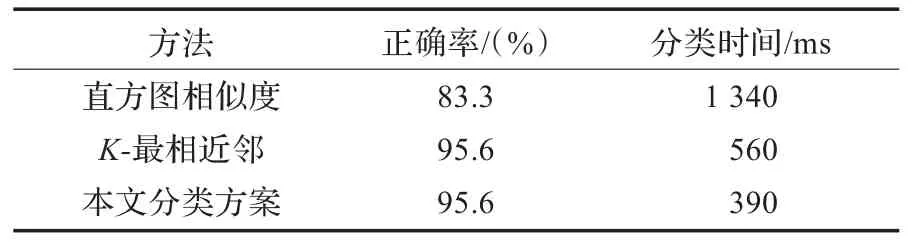
表3 地板分类识别方法的正确率及平均分类时间对比
6 结论
在HSV色彩空间提取出色调及饱和度的颜色矩特征数据,以加权的方式对地板样本的色调特征数据分配以较高的权重,减小地板纹理对分类准确性的影响。通过最大最小距离算法对相似地板样品类别进行聚类处理,建立层次分类样本库,减少K-最近相邻分类法的计算数据量,提高了未知地板样本的分类速度。针对K-最近相邻分类中属于最大近邻数对应的类别可能不只一个的问题,提出了K-最近相邻-最短距离法。测试结果表明,本文方案在保证K-最近相邻分类法正确率的基础上能够有效地减少地板分类所需要的时间。
[1]戴天虹,王克奇,杨少春.基于颜色特征对木质板材分级的研究[J].系统仿真学报,2008,20(5):1372-1376.
[2]王克奇,杨少春,戴天虹,等.基于均匀颜色空间的木材分类研究[J].计算机工程与设计,2008,29(7):1780-1784.
[3]罗玉娟,李熙莹,蔡志岗,等.采用均匀颜色空间的竹片分类研究[J].计算机工程与应用,2010,46(16):238-240.
[4]罗玮,彭复员,柳健.彩色瓷砖的自动分类系统[J].华中科技大学学报:自然科学版,2001,29(3):79-81.
[5]孙君顶,赵珊.图像低层特征提取与检索技术[M].北京:电子工业出版社,2009.
[6]徐琨,李燕.基于分块颜色矩和纹理特征的图像检索方法[J].西安石油大学学报:自然科学版,2005,20(2):77-79.
[7]周涓,熊忠阳,张玉芳,等.基于最大最小距离法的多中心聚类算法[J].计算机应用,2006,26(6):1425-1427.
[8]Cover T M,Hart P E.Nearest neighbor pattern classification[J]. IEEE Trans on Inform Theory,1967,13:21-27.
[9]Acharya T.Ray A K.Image processing principles and applications[M].Wiley-Interscience Publication,2005.
[10]Duda R O,Hart P E,Stork D G.Pattern classification[M]. 2nd ed.[S.l.]:Wiley-Interscience Publication,2000.
QIAN Yong,BAI Ruilin,NI Jian,DU Bin
Key Laboratory of Advanced Process Control for Light Industry(Ministry of Education),Institute of Intelligent Control,Jiangnan University,Wuxi,Jiangsu 214122,China
The floor hierarchical classification based on the color characteristics is proposed to improve the automate degree. Through clustering the pre-specified color characteristics of the floor sample,the broad categories and specific categories are created to determine the training samples.To classify the unknown floor samples,the first use of the shortest distance classification is to determine the general category of the sample,then uses the improved K-nearest neighbor classification to determine the specific categories.Test results show that the hierarchical processing program reduces the K-nearest neighbor of the data processing phase with a higher classification accuracy.
color moments;floor classification;maximum minimum distance algorithm;minimum distance classification; K-nearest-neighbor classification
为提高地板生产过程中分类处理的自动化程度及其快速性,提出了一种基于地板颜色特征的层次分类方法。在HSV色彩空间提取出地板的颜色矩特征,并给予色调特征数据以较高权重,降低纹理特征对分类的影响。在对未知样本分类时,利用预先建立的粗细两层分类依据库,采用最短距离决策、K-最近相邻对未知地板样本由粗到细进行逐层判定。测试结果表明,该分层处理方案在保证较高的分类正确率(95.6%)的基础上,有效地减少了K-最近相邻的数据处理量。
颜色矩;地板分类;最大最小距离算法;最短距离分类;K-最近相邻分类
A
TP391
10.3778/j.issn.1002-8331.1111-0069
QIAN Yong,BAI Ruilin,NI Jian,et al.Floor hierarchical classification research based on color characteristics.Computer Engineering and Applications,2013,49(13):245-247.
国家自然科学基金(No.60804013);“嵌入式机器视觉关键技术的研究与开发”产学研合作资助项目(No.11002)。
钱勇(1986—),男,硕士研究生,研究方向:嵌入式系统与智能仪器,图像模式识别;白瑞林(1955—),男,教授,博士生导师,研究方向:智能控制与嵌入式系统;倪健(1976—),男,硕士研究生,研究方向:嵌入式系统与智能仪器,图像匹配;杜斌(1986—),男,硕士研究生,研究方向:嵌入式系统与智能仪器,图像特征提取与识别。E-mail:qianyong-1986@163.com
2011-11-08
2012-01-02
1002-8331(2013)13-0245-03
CNKI出版日期:2012-04-25http://www.cnki.net/kcms/detail/11.2127.TP.20120425.1722.085.html

