蜜蜂交配优化算法在车间作业调度中的应用
李小霞,刘峰,刘建晓
华中农业大学 理学院,武汉 430070
蜜蜂交配优化算法在车间作业调度中的应用
李小霞,刘峰,刘建晓
华中农业大学 理学院,武汉 430070
1 引言
车间作业调度问题(JSP)所要解决的是如何找出多个工件在多台机器上的最优加工过程。JSP是许多企业在实际生产过程中都会面临的问题,也是一类典型的组合优化问题和NP难题[1-3]。目前,已经出现了多种用于求解该问题的方法,主要以启发式算法为主[4],例如:遗传算法[5-6]、模拟退火算法[7-9]、蚁群算法[10-11]等。尽管这些方法的应用已经取得了一定的效果,但由于仍然存在计算复杂度高,前期收敛速度快而后期收敛速度慢等问题,使得它们只适用于求解较小规模的车间作业调度问题,而且求解过程易陷入局部最优解。
蜜蜂交配优化算法(Honey-Bee Mating Optimization Algorithm,HBMOA)是近年来涌现出的一种新的群智能算法,其搜索最优解的方法受到真实蜜蜂交配过程的启示。蜂王是一个蜂群中最优秀、最健壮的个体,她的寿命长达3~5年,而工蜂和雄蜂的寿命最多只有5~6个月。蜂王飞出蜂巢与多个雄蜂在空中完成交配,交配后,雄蜂立即死亡,蜂王将飞回蜂巢产下幼蜂。幼蜂经工蜂精心培养,喂食蜂王浆,将成长为新一代蜂王。可见,蜜蜂交配繁衍过程是蜂王不断更新的过程,这一过程类似进化计算中的优化过程。模拟蜜蜂交配过程的算法——蜜蜂交配算法已经应用于解决多种组合优化问题[12-14],例如:水库优化问题、旅行商问题、车辆路径问题等,并得到了很好的优化结果。但是,至今尚未见到对于如何将蜜蜂交配优化算法应用于解决车间作业调度问题的具体实现方法的详细探讨。因此,本文在对车间作业调度问题进行详细描述的前提下,给出了将蜜蜂交配优化算法应用于车间作业调度问题的具体实现方法,并通过应用实例验证了该方法的可行性和有效性。
2 车间作业调度问题描述
假设有m台机器M={M1,M2,…,Mm},n个待加工工件P={P1,P2,…,Pn},工件Pi对应多道工序Oi={Oi1,Oi2,…,Oik},k≥1,矩阵JM中存放每道工序可选用的加工设备,即JM中任一元素JMij,1≤i≤n,1≤j≤k,表示第i个工件的第j道工序可选用的设备,矩阵T中存放每道工序在相应设备上的加工时间,即T中任一元素Tij,1≤i≤n,1≤j≤k,表示第i个工件的第j道工序在相应设备上加工所需的时间,则可将n/m车间作业调度问题的求解目标描述如下:
在满足加工约束条件的基础上,确定m台机器上n个工件的加工顺序,并使调度目标达到最优。
这里的加工约束条件一般包括:
(1)各工件之间无优先级;
(2)每个工件的各工序之间存在先后关系,即按照加工工艺规定,每道工序必须等到它前面的工序加工完毕后才能加工;
(3)在任一时刻,每台机器只能执行一道工序,且每道工序只能在一台机器上执行;
(4)每台机器在加工工序的过程中不会发生故障,加工不会中断。
本文采用最小化最大完工时间Cmax作为调度目标,满足公式(1):

其中Cij是工序Oij的加工结束时间。
3 车间作业调度问题的蜜蜂交配优化算法实现
蜜蜂交配优化算法是通过模拟蜜蜂交配过程实现全局寻优的。在蜜蜂交配过程中,蜂王飞出蜂巢,选择健壮的雄蜂进行飞行交配,每交配一次,蜂王就会将与之交配的雄蜂的基因存放在储精囊中,同时飞行速度也将减少一定的量。当蜂王的储精囊充满后,蜂王回到蜂巢,蜂王基因与储存在储精囊中的雄蜂基因进行交叉产下幼蜂,并将幼蜂交给工蜂抚养。若经工蜂抚养后的幼蜂比当前的蜂王更健壮,则它将替代当前蜂王成为新一代的蜂王,并开始它的交配飞行。由此可见,新蜂王的产生就是一个优化过程,而在蜜蜂交配过程结束后,所得到的蜂王即为待寻求的最优解。因此,可将蜜蜂交配过程应用于组合优化问题中寻求最优解。
通过蜜蜂交配寻求最优解的过程可以看出,蜜蜂交配算法应包括以下几个关键步骤:
(1)产生一个初始种群,并选择其中最健壮的个体作为蜂王,其他个体均作为雄蜂;
(2)选择能与蜂王交配的雄蜂;
(3)通过将蜂王的基因与雄蜂的基因进行交叉产生新的幼蜂;
(4)选择工蜂抚养幼蜂使其发生变异,并用变异得到的比当前蜂王更健壮的幼蜂替代当前蜂王;
(5)判断交配飞行次数是否达到最大值,若是则终止交配飞行,否则重复执行(2)、(3)、(4)。
基于以上分析,下面给出蜜蜂交配算法求解JSP的具体实现。
3.1 个体编码
一个车间作业调度方案对应一个个体编码串,该编码串包括三段内容:第一段对应的是全部工件的加工工序,第二段和第三段分别是执行第一段中各工序所选用的机器的序号和刀具的序号。
对于n/m车间作业调度问题,设n个工件中每个工件对应的工序数为ki(i为工件的序号),所有工件对应的工序之和S=k1+k2+…+kn,则编码的长度为3×S。编码的第一段为1..S部分,存放的是待加工的工件的序号,工件序号第j次出现即是工件的第j道工序,编码的第二段为S+1..2×S部分,存放的是第一段中各工序选用的机器在矩阵JM1中的序号,编码中第j(j<S)个位置的工序选用的机器号存放在编码的第j+S位置上,编码的第三段为2×S+1..3×S部分,存放的是第一段中各工序选用的刀具在矩阵JM2中的序号,编码中第j(j<S)个位置的工序选用的刀具号存放在编码的第j+2×S位置上。需要说明的是,矩阵JM2中存放每道工序可选用的刀具的序号,即JM2中任一元素JM2ij,1≤i≤n,1≤j≤k,表示第i个工件的第j道工序可选用的刀具。
3.2 初始种群的生成
通过上面的分析发现,蜂王是当前种群中最健壮的个体,而雄蜂也必须足够的健壮才能追上蜂王与之交配。因此,实现蜜蜂交配优化算法需要解决两个方面的问题:(1)如何生成一个健壮的初始种群;(2)如何从种群中选出最优的个体作为蜂王。
为了生成一个健壮的初始种群,选用遗传算法实现对随机生成的种群进行优化,优化所得的种群即为初始种群。通过遗传算法得到的初始种群是由多个健壮的个体组成的调度方案集,其中每一个个体分别对应为一个调度方案。为了从初始种群中选出最优的个体作为蜂王,采用公式(2)计算出个体的适应度并利用所计算出的适应度判断个体的优劣:

可见,调度方案所需时间越少,其适应度越高,方案越好。故而,可通过公式(2)计算出初始种群中各方案的适应度值,从中找出其中适应度最大的方案作为蜂王,其余方案作为雄蜂。
3.3 雄蜂选择的设计
蜂王以一定的速度飞出蜂巢,开始她的交配飞行。然而,由于蜂王的飞行速度较快,只有那些健壮的雄蜂才能追上她与之交配,也就是说,适应度越接近蜂王适应度的雄蜂与蜂王交配的概率越大,故而,可采用公式(3)计算雄蜂与蜂王交配的概率:

式中,f(Queen)-f(Drone)是蜂王与雄蜂的适应度之差,Speed(t)是蜂王在时刻t的速度,其初始值在蜂王开始交配飞行之前随机产生,并将随着时间的推移而不断降低,本文假设蜂王的速度以α为系数降低,即Speed(t+1)=α×Speed(t),α是随机产生的一个0到1之间的随机数。于是,根据公式(3)可计算出雄蜂与蜂王的交配概率,若交配概率满足条件Probility(Drone)>r,则雄蜂可与蜂王交配并将雄蜂的基因存放在蜂王的储精囊中。需要说明的是,条件中的r是一个随机产生的0到1之间的数。
3.4 交叉算子的设计
由于车间作业调度问题编码方式的特殊性,不能直接采用一般的交叉算子实现蜂王基因与雄蜂基因的交叉操作,而是将交叉算子具体设计为以下三个关键步骤:
(1)蜂王基因的第一段中的部分染色体与雄蜂对应的子染色体进行交叉;
(2)由于上一步骤中执行的交叉操作可能造成所得新染色体的前半段中出现缺失和多余的基因,因此要找出缺失和多余的基因,并用缺失的基因替换多余的基因,从而得到新染色体的第一段;
(3)根据新染色体前半段基因与蜂王和雄蜂的对应关系,得到新染色体的后两段基因。
3.5 变异算子的设计
由于不同工蜂会对幼蜂进行不同的抚养,因此,将不同工蜂对应为不同的变异方法,不同工蜂对幼蜂的抚养过程对应为不同的局部寻优过程。
假设工蜂数量为Domen(Domen≥1),则可通过生成一个的随机数m(m≤Domen)来选择相应的变异方法。这里将随机数m设置为变异的次数,根据存放在JM1和JM2中的各工件工序可选用的机器序号和刀具序号,对编码后两段的机器序号和刀具序号进行不同次数的变异。
4 实验与分析
为了验证本文提出的应用于车间作业调度的蜜蜂交配算法的可行性和有效性,采用文献[8]提供的实例作为测试用例,进行车间作业调度的蜜蜂交配算法的实验。其中所用的车间作业资源包括5台机器(M1,M2,…,M5),12个刀具(C1,C2,…,C12)可供选择使用,另有3个待加工的工件(编号为:1、2、3)以及它们对应的加工工序(工序个数为:20、16、14),可选用的机器和刀具,参见文献[15]。
仿真实验在Matlab中进行,在实验过程中,蜜蜂交配算法采用的雄蜂个数为100,交配飞行次数为800次,用于计算雄蜂与蜂王交配概率的参数Speed(t)的初始值设置为1 000,每交配一次速度下降的系数α设置为0.9。采用蜜蜂交配算法实现的调度甘特图如图1所示,可以看出,蜜蜂交配算法能够有效地求解车间作业调度问题。图2同时给出了采用蜜蜂交配算法、模拟退火算法和遗传算法实现测试用例中待加工工件所有工序的调度优化过程。从图2和表1的实验结果可以发现,蜜蜂交配算法用于解决JSP,能够得到比遗传算法和模拟退火算法更好的优化结果,是一种很有潜力的优化算法。

表1 算法优化结果
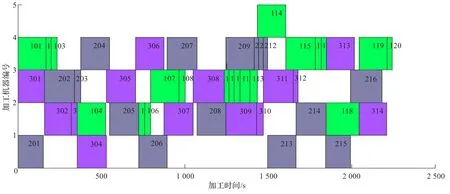
图1 蜜蜂交配算法调度甘特图

图2 算法优化过程
5 结束语
JSP是一类典型的组合优化问题。本文在对JSP进行详细分析的基础上,提出了一种用于求解JSP的蜜蜂交配算法。通过实例验证了蜜蜂交配算法求解JSP的可行性和有效性,同时将该算法与用于求解JSP的传统优化算法进行了实验比较,结果表明蜜蜂交配算法能够得到比传统优化算法更好的优化结果。然而,如何更科学地设定算法中的一些参数,以及将算法进一步应用于解决多目标车间作业调度问题,还有待今后进行更深入的研究。
[1]BlazewiczJ,FinkeG,HaoptG.Newtrendsinmachine scheduling[J].European Journal of Operational Research,1988,37:303-317.
[2]Martin D,Bracken I.The integration and socioeconomic and physical resource data for applied land management information systems[J].Applied Geo Graphy,1993,2:45-53.
[3]王凌.车间调度及其遗传算法[M].北京:清华大学出版社,2003:71-121.
[4]郭冬芬,李铁克.基于约束满足的车间调度算法综述[J].计算机集成制造系统,2007,13(1):117-125.
[5]Biegel J E,Davern J J.Genetic algorithms and job shop scheduling[J].Computers and Industrial Engineering,1990,19(4):81-91.
[6]纪树新.遗传算法在车间作业调度中的应用[J].系统工程理论与实践,1998,18(5):34-39.
[7]Plamer G J.A simulated annealing approach to integrated production scheduling[J].Journal of Intelligent Manufacturing, 1996,7(3):163-176.
[8]赵卫.模拟退火遗传算法在车间作业调度中的应用[J].计算机仿真,2011,28(7):361-364.
[9]Li W D,Ong S K,Nee A Y C.A hybrid genetic algorithm and simulated annealing approach for the optimization of process plan for prismatic parts[J].Int J Prod Res,2002,40:1899-1922.
[10]姬耀锋,党培,郭小波.基于蚁群算法的车间作业调度问题研究[J].计算机与数字工程,2011,39(1):4-6.
[11]王进峰,阴国富,雷前召,等.蚁群算法在工艺规划与车间调度集成优化中的研究[J].东南大学学报:自然科学版,2012,42(S1):173-177.
[12]Abbass H A.Marriage in honey-bee optimization(MBO):a haplometrosis polygynous swarming approach[C]//Proceedings of the Congress on Evolutionary Computation(CEC2001),Seoul,Korea,2001:207-214.
[13]Afshar A,Bozog Haddad O,Marino M A,et al.Honey-Bee Mating Optimization(HBMO)algorithm for optimal reservoir operation[J].JournaloftheFranklinInstitute,2007,344:452-462.
[14]Marinakis Y,Marinaki M.A honey bees mating optimization algorithmfor the openvehicle routingproblem[C]// Proceedingsof the13th Annual ConferenceonGenetic andEvolutionaryComputation(GECCO11),NewYork,USA,2011:101-108.
[15]Li W D,Ong S K,Nee A Y C.Optimization of process planning using a constraint-based tabu search method[J]. Int J Prod Res,2004,42:1955-1985.
LI Xiaoxia,LIU Feng,LIU Jianxiao
College of Science,Huazhong Agricultural University,Wuhan 430070,China
To solve the Job-shop Scheduling Problem(JSP),a solution method—honey-bee mating optimization algorithm is presented on the basis of the JSP’s description.The method takes a set of job scheduling schemes as the bee swarm,and minimizing the processing time as the optimization goal.The optimal scheduling scheme is obtained by simulating the procedure of honey-bee mating.The test is carried out by the JSP test cases on Matlab.The experimental results show that this method can not only solve JSP but also find a better optimal scheduling scheme than the traditional optimization methods.
honey-bee mating optimization algorithm;Job-shop Scheduling Problem(JSP);combinatorial optimization
为了解决车间作业调度问题,在对其进行分析描述的基础上,提出了采用蜜蜂交配优化算法的求解方法。该方法把由多个作业调度方案组成的集合作为蜂群,以最小化加工时间作为算法的优化目标,通过模拟蜂群交配繁衍培养蜂王的优化过程来获得最优作业调度方案。采用车间作业调度测试案例在Matlab平台上进行实验,实验结果表明,该方法不仅能够有效地求解车间作业调度问题,而且能够取得了比传统优化方法更好的优化结果。
蜜蜂交配优化算法;车间作业调度问题;组合优化
A
TP391
10.3778/j.issn.1002-8331.1303-0193
LI Xiaoxia,LIU Feng,LIU Jianxiao.Application of honey-bee mating optimization algorithm to job-shop scheduling. Computer Engineering and Applications,2013,49(13):262-265.
武汉大学软件工程国家重点实验室开放研究基金(No.SKLSE2012-09-24);华中农业大学新进博士科研启动专项(No.52902-0900206084,No.52902-0900206081);高等学校博士学科点专项科研基金新教师类资助课题(No.20120146120002);中央高校基本科研业务费专项资金资助项目(No.2013PY118)。
李小霞(1979—),女,博士,讲师,研究领域为CAD,CIMS;刘峰(1981—),通讯作者,男,博士,讲师,研究领域为CIMS,物联网;刘建晓(1985—),男,博士,讲师,研究领域为云制造。E-mail:lxx1818@126.com
2013-03-13
2013-06-08
1002-8331(2013)13-0262-04

