基于改进差分进化的车辆路径优化算法

邬开俊，王铁君

1.兰州交通大学 电子与信息工程学院，兰州 730070

2.西北民族大学 数学与计算机科学学院，兰州 730030

基于改进差分进化的车辆路径优化算法

邬开俊1，王铁君2

1.兰州交通大学 电子与信息工程学院，兰州 730070

2.西北民族大学 数学与计算机科学学院，兰州 730030

1 引言

车辆路径问题（Vehicle Routing Problem，VRP）是指由一组车辆从一个或多个车场点出发对分布在不同地理位置的一系列顾客点进行服务，要求每个顾客点的需求必须被满足，每个车辆的路线开始于车场点，并最终结束于车场点[1]。如图1所示，左图是一个有1个车场一系列顾客点的VRP的实际问题，右图为一种动用5辆车的可行方案。优化一般以动用车辆数尽可能少，以及所有车辆的总运行路线长度尽可能短为目标。它是组合优化和运筹学研究领域的热点问题之一，在现实生活中应用广泛，如城市垃圾收集，包裹配送，校车接送路线安排等。研究满足生产经营和运作需要的车辆路径问题，并构建具有高质量和高鲁棒性的问题求解算法，对于提高生产经营管理水平和降低运作成本具有重要的理论意义和现实价值。

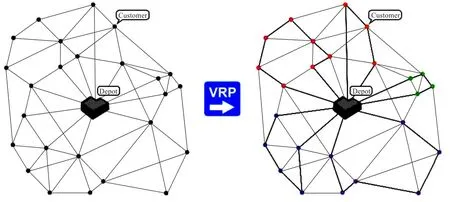
图1 一个VRP实例（左）及其可行解（右）

VRP是很多实际问题求解的最终转化形式，同时也是著名的NP难题，在短时间内精确地求出其最优解非常困难，尤其对于大规模问题，很难求得最优解。近年来，遗传、粒子群、蚁群、禁忌等算法在解决这一类问题时得到了初步的应用[2-5]，但是在求解精度和求解效率等方面还有待于提高。

差分进化算法（Differential Evolution，DE）是一种模拟“优胜劣汰，适者生存”的自然进化法则的仿生智能计算方法[6]。DE在解决复杂的全局优化问题方面的性能更加优秀，过程也更为简单，受控参数少，被视为仿生智能计算产生以来在算法结构方面取得的重大进展[7-8]。针对该算法存在收敛速度缓慢，计算量大，易早熟等问题[9]，本文提出了一种改进的差分进化算法。实验结果表明，改进DE算法能够高效地解决VRP问题。

2 VRP的数学模型

从图论的角度来看，VRP可以被表示为：一个完备图G=(V，A)，V={0，1，…，n}表示顶点集，其中0表示车场，V′={1，2，…，n}表示顾客点集，A={(i，j)|i，j∈V，i≠j}表示边集。

定义如下变量：

式中，Z表示目标函数；Z1、Z2分别表示使用车辆数和所有车辆的总运行路线长度；k1、k2为其权值系数；ci，j是边(i，j)的权重，表示点i到点j的旅行费用；di，j是点i到点j的空间距离；Q是车辆的最大装载能力；needi是顾客点i的需求；m是服务车辆数；R是车辆集，R={1，2，…，m}。

约束条件中，式（4）表示每个顾客点都要服务到；式（5）表示每个顶点进出车辆数相等；式（6）表示每个顾客点只能由一辆车来服务；式（7）表示车辆不能超载，即每辆车所服务的顾客点的需求之和不能超过车辆最大装载能力Q；式（8）表示顾客点j只能由来自其他顾客点i的车辆中的一辆来服务。

3 基于改进DE的VRP求解算法

3.1 编码方式

编码方式采用简单直观的序号编码。顾客点序号集为{1，2，…，n}，车场序号为0，车辆数目为k。编码结构为：{v1,v2,…,vi,…,vn+k-1}，是由顾客点序号集{1，2，…，n}和(k-1)个0任意组合而成的。其中(k-1)个0的加入是为了区分不同车辆的行驶路线。

解码方式为：

（1）在每条编码的两头各加一个0；

（2）依次遍历每条编码，将编码中被0隔开的每段非0序列保存，即为一辆车的访问路径。

每条编码可解码出1至k辆车的路径来。

以9个顾客点，5辆车为例，编码X=（0，1，2，3，0，0，4，5，6，0，7，8，9），解码出：（1，2，3），（4，5，6），（7，8，9）三段非0序列，即此编码表示：动用了3辆车，分别按照（1→2→3），（4→5→6），（7→8→9）的路线行驶。

编码中不能出现负数、小数编码和非0位位值重复等问题，即存在合法化问题。这也正是变异操作后需要进行的合法化处理的原因。

3.2 适应度函数

适应度函数按式（1）定义：使用车辆数Z1和所有车辆的总运行路线长度Z2的加权和。权值系数k1、k2的取值根据具体情况进行设置，即若优先考虑使用车辆数目少，则可设置k1≫k2；若优先保证车辆总行驶距离短，则可设置k1≪k2。

3.3 种群的初始化

为提高初始种群的质量，采用贪婪的初始化方法。对于初始种群的每个个体，产生方法如下：

步骤1初始化待服务的顾客点列表List为包含所有顾客点序号的列表，已经服务的顾客点列表SList为空。

步骤2随机选择一个顾客点A作为起点，并将此点作为当前顾客点T，插入SList，并从List中移除。

步骤3从List中选择距离顾客点T最近的顾客点作为新的当前顾客点T，将T插入SList，并从List中移除。

步骤4判断List是否为空，若是，则转步骤5；若否，则转步骤3。

步骤5将(K-1)个0随机插入SList序列中。

步骤6判断SList是否满足所有的约束条件，若不满足，则跳至步骤1；若满足，则结束。

通过以上贪婪方法初始化初始种群，直接得到局部较优解，能够大幅加快收敛速度。

3.4 变异及其合法化处理

将随机选择的个体进行直接按位相加减，而后进行合法化处理。

对于5个顾客点，2辆车的例子，随机选择3个个体：（1，0，2，3，0，4，5），（2，5，0，3，1，0，4），（5，3，1，0，0，4，2）。

合法化处理过程：

（1）提取编码vi中的0并记录其位置。如果0值位超过车辆数，则只提取车辆数个0。此时，vi=(-2，2，1，6，1，7)。

（2）将提取过0的编码vi从小到大排序，然后使用其序号代替原编码值。

如：vi=(-2，2，1，6，1，7)，排序后为：(-2，1，1，2，6，7)。从前到后依次：位值-2的序号为1，位值2的序号为4，依次类推进行合法化处理后的编码为（1，4，2，5，3，6）。

（3）将步骤（1）中提取出的0重新插入编码。此时vi=（1，4，2，5，3，0，6）。

3.5 改进的贪婪顺序交叉

顺序交叉可以看做是带有不同修复程序的部分映射交叉PMX的变形，能够较好地保留相邻关系、先后关系[10]。改进主要是针对编码中0值位可能出现重复的问题，即在去掉已有基因时，从前往后进行删除，并且，已有基因中有几个0则删除几个0。其步骤如下：

步骤1选切点c1、c2。

步骤2交换中间部分。

步骤3从第二个切点c2后，第一个基因起列出原顺序，去掉已有基因（注意0的个数）。

步骤4从第二个切点c2后，第一个位置起，将获得的无重复顺序填入。

以上步骤可以用图2来说明。

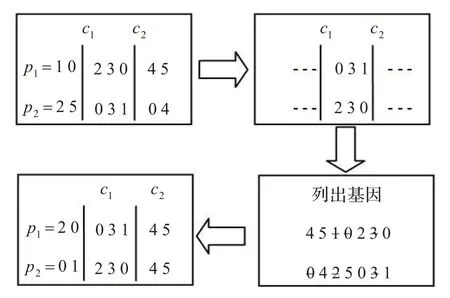
图2 交叉运算示意图

每次顺序交叉会产生两个交叉个体，而DE交叉操作中只需要一个交叉个体，为了提高收敛速度，改进算法贪婪选择适应度更优的个体作为返回的交叉个体。

3.6 选择操作及流程的改进

基本差分进化算法变异操作之后，直接进行交叉操作，可能导致变异操作产生的优良基因被交叉操作所破坏。为了防止交叉操作消除或者影响变异操作产生的寻优效果，改进算法在保留原有交叉操作之后的贪婪选择机制之外，增加了变异操作之后的选择机制，即：如果变异个体的适应度优于原个体，则直接跳过交叉操作，选择变异个体进入下一代种群；否则，如果变异个体劣于原个体，按照基本差分进化算法的流程，在变异的基础上进一步进行交叉操作。

3.7 改进DE算法的总流程

步骤1初始化参数。令迭代次数t=0，设置最大迭代次数，种群规模NP，放缩因子F，以及交叉常数CR。

步骤2贪婪初始化。

步骤3循环次数t←t+1。

步骤4令目标个体索引号i=1。

步骤5在目标个体xi之外随机选择另外3个不同的个体。

步骤6执行变异操作，产生变异个体vi。

步骤7计算vi的适应度，执行选择操作，若变异个体vi优于目标个体xi，则跳转到步骤10；否则执行步骤8。

步骤8对xi和vi执行交叉操作，产生交叉个体ui。

步骤9计算ui的适应度，执行选择操作。

步骤10目标个体索引号i←i+1，返回步骤5直至i=NP；否则，执行步骤11。

步骤11若迭代次数大于最大迭代次数，则循环结束并输出计算结果；否则跳转到步骤3，继续下一次迭代。

4 实验

为了证明改进DE算法的实用性和有效性，使用Matlab语言环境编程实现了改进算法，选用国际通用的VRP测试数据集实例：A-n32-k5.vrp（http：//www.coin-or.org/SYMPHONY/branchandcut/VRP/data/）进行求解，并与基本差分进化算法和基本蚁群算法进行了对比。测试数据集中顾客点的坐标和需求，如表1所示。

车场位置坐标(X，Y)=(82，76)，车辆总数为8辆，车辆最大载重Q=100 t。

设置改进DE算法的参数：种群规模NP为100，最大迭代次数为500，差分进化算法的交叉概率CR为0.5，放缩因子F为1，k1=1000，k2=1。

运行改进DE算法的最优个体为：（21，31，19，17，13，7，26，0，0，0，12，1，16，30，0，27，24，0，0，29，18，8，9，22，15，10，25，5，20，0，14，28，11，4，23，3，2，6），解码如表2所示。

表1 顾客点的坐标和需求

表2 最优个体的解码结果

所需车辆数为5，所有车辆路线长度之和为787.81 km，每辆车的载重均小于100 t，符合约束条件。此解也是该数据集实例目前已知的最优解，具体路线如图3所示。

图3 最优解示意图

改进DE算法与基本蚁群算法、基本DE算法进化过程对比，如图4所示。从图可知，在进化前期，改进DE算法与基本蚁群算法和基本DE算法都迅速优化，基本DE算法优化较慢；在进化后期时，基本蚁群算法和基本DE算法收敛速度慢，而改进DE算法能够不断优化，更快地在有限迭代次数里搜索到了最优解。因此，证明了本文改进DE算法求解VRP时的良好性能。

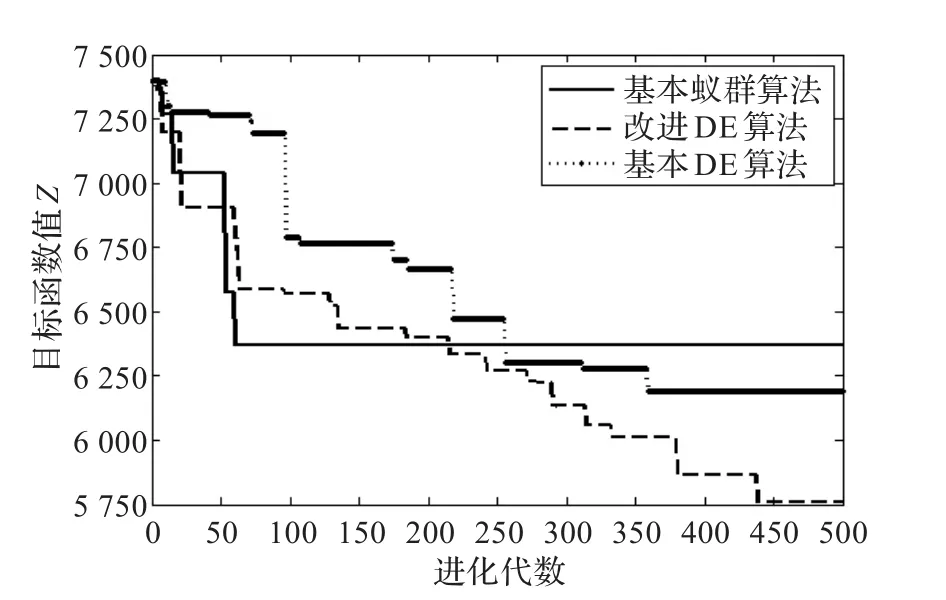
图4 进化过程对比

5 结束语

提出了一种将差分进化算法应用于VRP问题的新的改进方法。实验证明了改进的DE算法针对VRP问题的良好性能。但本文求解的标准VRP是VRP问题中约束条件最少的情况，下一步将进一步增加约束机制，改进模型，从而应用于更为复杂的VRP问题。

[1]Dantzig G，Ramser J.The truck dispatching problem[J].Management Science，1959（6）：58-102.

[2]陈迎欣.基于改进蚁群算法的车辆路径优化问题研究[J].计算机应用研究，2012，29（6）：2031-2034.

[3]王铁君，邬开俊.带时间窗的多车场车辆路径优化的粒子群算法[J].计算机工程与应用，2012，48（27）：27-30.

[4]蒋波.基于遗传算法的带时间窗车辆路径优化问题研究[D].北京：北京交通大学，2010-06.

[5]王君，李波.带模糊预约时间的车辆路径问题的多目标禁忌搜索算法[J].计算机集成制造系统，2011，17（4）：858-866.

[6]Storn R，Price K.Differential evolution-a simple and efficient adaptiveschemeforglobaloptimizationovercontinuous spaces，TR-95-012[R].Berkley：International Computer Science Institute，1995.

[7]Vesterstorm J，Thomsen R.A comparative study of differential evolution，particle swarm optimization and evolutionary algorithm on numerical benchmark problem[C]//Proceedings of IEEE Congress on Evolutionary Computation，2004：1980-1987.

[8]段海滨，张祥银，徐春芳.仿生智能计算[M].北京：科学出版社，2011：107-127.

[9]刘波，王凌，金以慧.差分进化算法研究进展[J].控制与决策，2007，22（7）：721-729.

[10]汪定伟.智能优化方法[M].北京：高等教育出版社，2007：38-39.

WU Kaijun1,WANG Tiejun2

1.School of Electronic and Information Engineering,Lanzhou Jiaotong University,Lanzhou 730070,China
2.School of Mathematics and Computer Science Institute,Northwest University for Nationalities,Lanzhou 730030,China

As a new kind of evolutionary algorithm,Differential Evolution（DE）algorithm with the characteristics of remembering individual optimal solution and information sharing can be regarded as a real coded and excellent security greedy genetic algorithm.To solve the Vehicle Routing Problem（VRP）,which belongs to NP problems,the paper puts forward an improved differential evolution algorithm.A greedy algorithm is used to generate the initial population,legalized method is used to repair mutation,improved order crossover is used,then,after the mutation operator,a new selection mechanism is added in.The new algorithm is implemented in Matlab,the experimental results show that the improved differential evolution algorithm can efficiently solve the VRP.

Differential Evolution（DE）;Vehicle Routing Problem（VRP）;greedy algorithm;NP problem;evolutionary algorithm

差分进化算法是一种具有记忆个体最优解和种群内部信息共享的特点的新型进化算法，本质上可看做是一种基于实数编码的、具有保优思想的贪婪遗传算法。针对具有NP难的车辆路径优化问题，提出了一种改进的差分进化算法。利用贪心算法产生初始种群，定义合法化修复变异个体的方法，采用改进的顺序交叉，并在变异操作之后，加入新的选择机制。使用Matlab进行了算法的实现，实验结果表明了改进DE算法能够高效地解决VRP问题。

差分进化算法；车辆路径问题；贪心算法；NP问题；进化算法

A

TP301.6

10.3778/j.issn.1002-8331.1301-0363

WU Kaijun,WANG Tiejun.Vehicle Routing Problem algorithm based on improved differential evolution.Computer Engineering and Applications,2013,49（13）：17-20.

国家社科基金（No.12CGL004）；兰州交通大学青年科学研究基金（No.2011005）。

邬开俊（1978—），男，博士研究生，副教授，CCF会员，研究方向：智能优化算法，应急调度；王铁君（1981—），女，博士研究生，讲师，CCF会员，研究方向：智能优化算法，车辆路径优化。E-mail：wkj@mail.lzjtu.cn

2013-02-05

2013-04-05

1002-8331（2013）13-0017-04

CNKI出版日期：2013-04-11http://www.cnki.net/kcms/detail/11.2127.TP.20130411.1555.003.html