效应代数成为布尔代数的充要条件
李海洋
西安工程大学 理学院,西安 710048
效应代数成为布尔代数的充要条件
李海洋
西安工程大学 理学院,西安 710048
1 引言
计算机硬件以惊人的速度增长,以致1965年Moore把这种增长概括为Moore律,即计算机的能力以固定的速率成长,大约每两年增加一倍。从20世纪60年代开始Moore律在几十年时间里都近似成立,然而,大多数观察家预期这将在21世纪的前20年内结束。当电子器件越做越小时,它的功能开始受到量子效应的干扰。
众所周知,量子逻辑是量子计算和量子力学的数学基础。效应代数作为量子逻辑的数学模型由Foulis和Bennett在1994引入[1]。与此同时,Kopka和Chovanec独立地引入了一种称之为D-偏序集的代数结构[2]。实际上,这两种代数结构是等价的。自1994年以来,文献[3-10]分别研究了效应代数中的sharp元、中心元、理想以及同余等代数性质。作为这些研究的继续,本文首先通过效应代数的中心元引入效应代数中的Well Inside关系,并在此基础上给出了一个效应代数成为布尔代数的充要条件。
2 预备知识
本章给出一些需要的主要定义,其他的请参考文献[11]。
定义1设E是一个含有特殊元0,1(0≠1)的集合,分别称为零元和单位元,⊕是E上的一个部分二元运算,并满足如下公理,其中a,b,c∈E。
(E1)(交换律)如果a⊕b有定义,则b⊕a有定义且a⊕b=b⊕a;
(E2)(结合律)如果b⊕c有定义且a⊕(b⊕c)有定义,则a⊕b有定义,(a⊕b)⊕c有定义,且a⊕(b⊕c)=(a⊕b)⊕c;
(E3)(正交补律)对任意a∈E,存在唯一b∈E使得a⊕b有定义且a⊕b=1;
(E4)(0-1律)如果1⊕a有定义,则a=0,那么称代数系统(E,⊕,0,1)为效应代数。
通常将效应代数(E,⊕,0,1)简记为E。设E为效应代数,a,b∈E。若a⊕b有定义,则称a垂直于b,并记做a⊥b。条件(E3)中唯一的b∈E称为a的正交补,记作a′。
在E中定义a≤b,当且仅当存在c∈E,使得b=a⊕c。则对任意效应代数E,容易证明(见文献[1]):
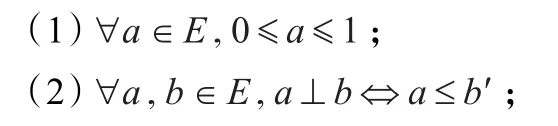
(3)(E,⊕,0,1)是偏序集且满足所谓的正交模律:
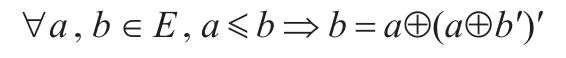
若偏序集(E,⊕,0,1)还是一个格,则称E为格序效应代数。此外,若a,b∈E,且a⊕b和a∨b存在,则a∧b也存在且a⊕b=(a∨b)⊕(a∧b)。反之,若a⊕b和a∧b存在,则a∨b不一定存在(见文献[7]例2.14)。
定义2(1)设E是效应代数,子集Q⊂E被称为E的子-效应代数,当且仅当0,1∈Q,且Q对p↦p′(∀p∈Q)封闭,以及对任意p,q∈Q,p⊥q⇒p⊕q∈Q。
(2)E的子-效应代数Q被称为正规子-效应代数,当且仅当对任意a,b,c∈E,若a⊕b⊕c∈E,a⊕b∈Q,且b⊕c∈Q,则b∈Q。
定义3设E是效应代数,且a∈E,a≠0,在区间F=[0,a]={b∈E|b≤a}上定义二元关系⊕F如下:∀b,c∈F,b⊕Fc有定义,当且仅当b⊥c且b⊕c≤a,则(F,⊕F,0,a)是效应代数。尽管F中的偏序与E中的偏序一致(事实上,F中的偏序是E中的偏序在F是上的限制),但F和E中的正交关系并不相同,它们具有如下的关系:

其中,*为F中的正交补。
E中的元素p称为主元,当且仅当⊥F是⊥在F=[0,a]上的限制。因此,p是主元当且仅当x⊥y蕴含x⊥Fy (∀x,y∈F)。再或者,p是主元当且仅当x⊥y,x,y≤p蕴含x⊕y≤p。
定义4设E、F是效应代数,映射f:E→F称为效应代数态射,如果它满足下面的条件:
(1)f(1E)=1F;(2)若a,b∈E,a⊥b,则f(a)⊥f(b)且f(a⊕b)=f(a)⊕f(b)。若效应代数态射f是一一映射,且f-1也是效应代数态射,则称f是效应代数同构。
易知效应代数的笛卡尔积按照点式序仍旧构成效应代数。因此若c∈E,则[0,c]×[0,c′]是效应代数,从而存在映射:
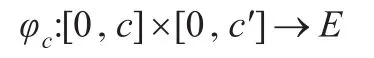
具体为φc(x,y)=x⊕y(∀x∈[0,c],y∈[0,c′])。
若φc是效应代数同构,则称c为E的中心元。E中的所有的中心元组成的集合称为E的中心,并记为C(E)。
关于效应代数的中心元和中心,有以下结论:
引理1[4]效应代数E中的元素c是中心元当且仅当下面条件成立:
(1)c和c′都是主元;
(2)对每个a∈E,有a=a1⊕a2且a1≤c,a2≤c′。
此外,可以证明(2)中的a1和a2是唯一的,并且a1=a∧c,a2=a∧c′。
引理2[8]若效应代数E是格序的,则c∈C(E),当且仅当a=(a∧c)∨(a∧c′)(∀a∈E)。
引理3[4]效应代数E的中心C(E)是E的Boolean子代数,且若c,d∈C(E),则c,d在C(E)中的交、并与在E中的交、并一致。
引理4[4]若c∈C(E)且a∈E,则x=a∧c,y=a∧c′都在E中存在,且x∧y=0,x⊕y=x∨y=a。特别地,若c∈C(E),a∈E则c⊥a,当且仅当a∧c=0。
定义5设E是效应代数。
(1)E的子集I称为理想,若I满足以下条件:
(i)对任意a∈E,r∈I,a≤r⇒a∈I;
(ii)对任意r,s∈I,若r⊕s有定义,则r⊕s∈I。
(2)E中的理想I称为是Riesz理想,若对任意a,b∈E,r∈I满足r≤a⊕b,则存在ra,rb∈I使得ra≤a,rb≤b且r≤ra⊕rb。
3 效应代数中的Well Inside关系
本章首先引入效应代数中的Well Inside关系,并在此基础上给出了一个效应代数成为布尔代数的充要条件。
定义6设E为效应代数,a,b∈E。如果存在c∈C(E)使得a∧c=0且b∨c=1,则称aWell Insideb,并记为a≺b。
定理1设E为效应代数,则:
(1)对任意a∈E,0≺a,a≺1;
(2)对任意a∈E,a≺a,当且仅当a∈C(E);
(3)若a≺b,则a≤b;
(4)对任意a,b,c,d∈E,若a≤b≺c≤d,则a≺d;
(5)若a≺b,c≺d且,则a⊕c≺b⊕d;
(6)若a≺b,c≺b且a⊥c,则a⊕c≺b;
(7)令Ia={x∈E|x≺a},则Ia是E的Riesz理想。
证明(1)显然成立。
(2)设a≺a,则由定义6可知,存在c∈C(E)使得a∧c=0且a∨c=1。再由引理1,a=(a∧c)⊕(a∧c′)=a∧c′,从而a≤c′,因此a⊕c有定义,所以有a⊕c≥a∨c=1,即a是c的补元,再由引理3可知a∈C(E);反之,若a∈C(E),取c=a′∈C(E),则可证结论成立。
(3)若a≺b,则由定义6,存在c∈C(E)使得a∧c=0且b∨c=1,从而b′∧c′=0,因此由引理4,a⊥c,b′⊥c′,所以a≤c′,c′≤b,即a≤b。
(4)由b≺c可知存在x∈C(E)使得b∧x=0且c∨x=1;又a≤b,c≤d,所以a∧x≤b∧x=0且d∨x≥c∨x=1,从而a≺d。
(5)若a≺b,c≺d,则存在x,y∈C(E)使得a∧x=0且b∨x=1,c∧y=0且d∨y=1,从而b′∧x′=0,d′∧y′=0,因此由引理4,a⊥x,b′⊥x′,c⊥y,d′⊥y′,所以a≤x′≤b,c≤y′≤d;又d⊥b,所以a⊕c,x′⊕y′有定义,且a⊕c≤x′⊕y′≤b⊕d。取z=(x′⊕y′)′,则z∈C(E),且(a⊕c)∧z=0,(b⊕d)∨z=1,因此a⊕c≺b⊕d。
(6)若a≺b,c≺b,则存在x,y∈C(E)使得a∧x=0且b∨x=1,c∧y=0且b∨y=1,从而b′∧x′=0,b′∧y′=0,因此由引理4,a⊥x,b′⊥x′,c⊥y,b′⊥y′,所以a≤x′≤b,c≤y′≤b;再由引理3,x′∨y′∈C(E),则a⊕c≤x′∨y′≤b。取z=(x′∨y′)′=x∧y,则z∈C(E),且(a⊕c)∧z=0,b∨z=1,因此a⊕c≺b。
(7)由上面(4)和(6),则有Ia是E中的理想。下面证Ia是E的Riesz理想。
若e∈Ia,b,c∈E满足b⊥c且e≤b⊕c,则存在d∈C(E)使得e∧d=0且a∨d=1,从而a′∧d′=0,因此由引理4,e⊥d,a′⊥d′,所以e≤d′≤a,从而e≤(b⊕c)∧d′=(b∧d′)⊕(c⊕d′)。又b∧d′,c∧d′∈Ia,所以Ia是E的Riesz理想。
定理2设E是完备的效应代数,则以下各条等价:(1)E是布尔代数;
(2)对任意x∈E,Ix={y∈E|y≺x}=↓x={y∈E|y≤x};(3)对任意x∈E,x=∨Ix=∨{y∈E|y≺x}。
证明(1)⇒(2)⇒(3)显然成立。下面证(3)蕴含(1)。

[1]Foulis D J,Bennett M K.Effect algebra and unsharp quantum logics[J].Found Phys,1994,24:1331-1352.
[2]Kopka F,Chovanec F.D-posets[J].Mathematical Slovaca,1994, 44:21-34.
[3]Jenca G,Riecanova Z.On sharp elements in lattice ordered effect algebras[J].BUSEFAL,1999,80:24-49.
[4]Greechie R,Foulis D,Pulmannova S.The center of an effect algebra[J].Order,1995,12:91-106.
[5]Gudder S.S-dominating effect algebras[J].International Journal of Theoretical Physics,1998,37:915-923.
[6]Riecanova Z.Continuous lattice effect algebras admitting ordercontinuous states[J].Fuzzy Sets and Syetems,2003,136:41-54.
[7]Riecanova Z.Sharp elements in effect algebras[J].International Journal of Theoretical Physics,2001,40:913-920.
[8]Riecanova Z.Subalgebras,intervals and central elements of generalized effect algebra[J].International Journal of Theoretical Physics,1999,38:3209-3220.
[9]颉永建.具有Riesz分解性质的广义效应代数[J].陕西师范大学学报:自然科学版,2009(3):1-4.
[10]颉永建,李永明。由可精确测量元控制的弱可换的伪效应代数[J].计算机工程与应用,2008,44(34):23-25.
[11]Dvurecenskij A,Pulmannova S.New trends in quantum structures[M].Kluwer:Dordrecht Academic Publishers,2000.
[12]Avallone A,Vitolo P.Congruences and ideals of effect algebras[J].Order,2003,20(1):67-77.
LI Haiyang
School of Science,Xi’an Polytechnic University,Xi’an 710048,China
The relationship of Well Inside in effect algebra is introduced by the center elements of effect algebra,and the properties of the relationship of Well Inside are studied.Based on the relationship of Well Inside,a necessary and sufficient condition which effect algebra becomes Boole algebra has been obtained.
effect algebra;Boole algebra;relationship of Well Inside
通过效应代数中的中心元引入效应代数中的Well Inside关系,研究了效应代数中的Well Inside关系的性质;在此基础上得出了效应代数成为布尔代数的一个充要条件。
效应代数;布尔代数;Well Inside关系
A
O153.1
10.3778/j.issn.1002-8331.1301-0271
LI Haiyang.Necessary and sufficient condition which effect algebra becomes Boole algebra.Computer Engineering and Applications,2013,49(13):5-7.
国家自然科学基金(No.11271297);陕西省教育厅专项基金(No.12JK853)。
李海洋(1975—),男,博士,副教授,主要研究领域为格上拓扑学,量子逻辑。E-mail:fplihaiyang@126.com
2013-01-24
2013-03-19
1002-8331(2013)13-0005-03
CNKI出版日期:2013-03-29http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1701.022.html

