MIMO-OFDM系统的IFD-SAGE信道估计算法
高敬鹏,赵旦峰,周相超,付芳
哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001
MIMO-OFDM系统的IFD-SAGE信道估计算法
高敬鹏,赵旦峰,周相超,付芳
哈尔滨工程大学 信息与通信工程学院,哈尔滨 150001
1 引言
正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)技术与多输入多输出(Multiple Input Multiple Output,MIMO)技术相结合已经成为第四代移动通信系统的关键技术之一[1-2]。为了实现MIMO-OFDM系统优良的传输性能,在解调之前进行精确的信道估计是非常必要的。目前在MIMO-OFDM系统的信道估计研究领域中,信道估计方法一般分为三种:非盲信道估计[3]、盲信道估计[4]和半盲信道估计方法[5]。半盲信道估计是非盲信道估计算法和盲信道估计算法的折中算法,既能提供良好的算法性能,又能很好地克服非盲信道估计算法的频谱利用率低和盲信道估计算法相位模糊以及收敛速度慢等缺点。
近年来,半盲信道估计算法因在信道信息不准确的条件下具有优越性能而得到迅速发展。文献[6-7]分别提出了最优最小二乘(Least Square,LS)和最优线性最小均方误差(Linear Minimum Mean Square Error,LMMSE)算法,并且在多个OFDM符号间采用相位正交导频序列以增加频谱利用率。虽然算法设计简单,但仍需矩阵求逆运算,且很难达到理想的估计性能。文献[8]利用Turbo迭代技术在信道估计上得到了很好的性能,但是该算法应用范围较小,且具有较高的复杂度。文献[9-10]给出了基于期望最大化算法的半盲信道估计算法,利用不完整数据集通过迭代得到估计值,但是该算法在每次迭代时需要更新整个参数集信息,其算法复杂度较高同时对迭代初值要求较高。文献[11]在MIMO-OFDM系统下提出了频域的空间交替广义期望最大化(Frequency Domain Space-Alternating Generalized EM,FD-SAGE)算法,并对它的均方误差性能和收敛性进行了分析。为了改善FD-SAGE算法的系统信道估计性能以及收敛速度问题,本文首先在FD-SAGE算法的基础上,通过对SAGE算法的完整数据空间进行贝叶斯公式分解推导出一种修正的SAGE算法,提高了算法的估计性能。然后,在迭代的最大值步骤操作中引入最大似然算法对OFDM符号进行估计,以提高算法的估计性能和收敛速度。
2 系统模型
MIMO-OFDM系统模型如图1所示。在发射端,数据源中的数据经信道编码模块后,进行串并转换分解成多个子数据流,每个子数据流进行映射编码、插入导频、IFFT变换及加入循环前缀CP以完成OFDM组帧,再进行上变频,最后由多根发射天线同时发送出去。在接收端,信道空间传输的信号经过天线接收,通过下变频后,去掉循环前缀,进行FFT变换提取导频信号,利用导频信息对信道进行估计,然后通过信号检测和空时解码,信道译码数据经解映射、解交织及解码后送至信宿。

图1 MIMO-OFDM系统模型图
在MIMO-OFDM系统的发射端,发射天线mT上的调制信号经过IFFT后成为时域信号,并插入循环前缀(CP)以消除ISI。对于接收端去除收到时域信号的循环前缀并对其进行FFT变换后,在n时刻,第mR根接收天线上接收到的数据可以表示成:

3 信道估计算法过程
3.1 SAGE算法
SAGE算法[12]是一种广义空间迭代期望最大化算法,与文献[13]提出的(Expectation Maximization,EM)算法相类似,都是通过引入潜在数据将完全数据与观测数据建立起多对一的映射。建立映射关系后,与EM算法不同是,SAGE算法在每次迭代时仅更新估计参数集合中的某一个集合。

3.2 改进的FD-SAGE算法
文献[11]将SAGE算法应用到MIMO-OFDM系统中,提出了FD-SAGE算法,其算法通过迭代的方式将多天线的最小二乘(LS)信道估计问题转变成多个单天线系统的LS信道估计问题,避免了大矩阵的求逆运算,从而降低了系统的复杂度。但是由于LS本身的算法缺陷导致该算法的性能下降。根据SAGE算法,重新定义完全数据空间Z,接收信号Y为不完全数据,发送数据X为潜在数据,H为待估计量。改进的FD-SAGE算法(IFD-SACE)如下所示。

选择信道矩阵的第mR列作为要估计参数的子集,首先进行SAGE算法的E步操作,根据贝叶斯公式,可以得到:

由于lgp(X|HmR,H[i]mˉR)独立于H,在M步中只是进行极大化,可以将其忽略,式(6)可以分解为:

进行SAGE算法的M步操作,根据混合高斯模型,极大化式(8)。令关于的微分运算等于零,再对微分运算公式两边求共轭运算,忽略无关项,可以得到:

在第i+1次迭代时,更新的第mT根发射天线和第mR根接收天线之间的信道冲激响应:

然后,根据最大似然(ML)准则[14],通过更新符号检测值:
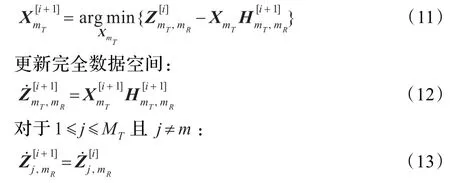
重复SAGE算法的迭代操作,直到迭代差值充分小或者达到设定的最大迭代次数时完成迭代过程。
3.3 导频的信道估计
对于改进的FD-SAGE算法来说,要想得到准确的信道状态信息并使算法快速收敛,信道估计初值的精准是十分重要的。MIMO-OFDM系统在发送数据时,以帧为单位进行数据传输,在每帧帧头都存在一个训练符号子块,接收时系统将去掉保护间隔的OFDM符号经过OFDM解调后,将接收码符号分成n+1个子块,第一个子块为已知导频信息,其他子块为n个OFDM符号。根据每一帧前端已知的块状导频数据,对于接收信号基于LS的信道估计为:

对于MIMO-OFDM系统来说,循环前缀的长度一般都大于信道的冲击响应长度。LS信道估计算法得到的信道能量集中在开头一些抽样点上,通过把大于循环前缀长度的信道响应值置零消除噪声的影响。将LS信道估计值进行IDFT变换得到:

式中,IDFTN{·}是N点的IDFT变换。所有有用的信道信息都包括在前LCP个抽样点上,其余的抽样点都是纯粹噪声。因此只保留前LCP个抽样点,忽略噪声区间。其响应用方程表示为:

在改进的FD-SAGE算法中,信道的初估计是由数据帧头的训练符号通过DFT-LS算法得到的,而后的OFDM符号都是以前一个符号的信号检测值和信道估计值作为后一个符号的导频信号来处理,即作为后一个符号的IDF-SAGE算法估计初值来处理,通过迭代实现信道估计。
4 仿真和分析
对本文所提的改进FD-SAGE算法设计方案进行系统性能仿真,仿真参数取值如表1所示。同时,假设发送天线和接收天线都相互独立,并且一帧内信道参数基本保持不变。
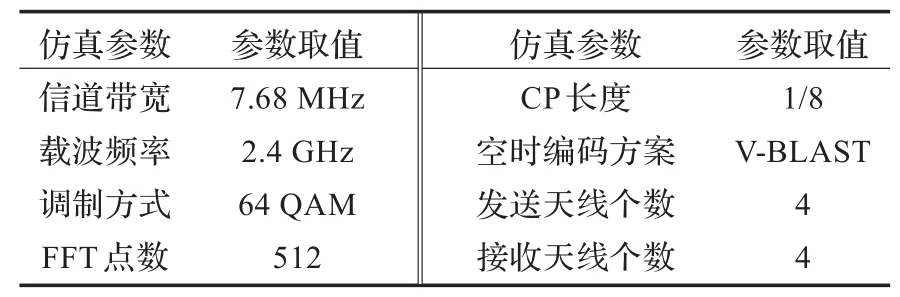
表1 算法仿真参数设置表
图2给出了采用LS信道估计与不同迭代次数的FD-SAGE信道估计和本文提出的IFD-SAGE算法,在设定的仿真参数条件下,均方误差性能随信噪比的变化曲线。仿真结果表明:在相同的迭代次数条件下,IFD-SAGE算法的性能明显优于FD-SAGE算法,原因是FD-SAGE算法随着信噪比逐渐增大时,由于地板效应使得算法的均方误差性能无法持续提高,而LS算法的估计性能由于受噪声方差影响,随着信噪比的提高而提高[15];与FD-SAGE算法相比,改进的FD-SAGE迭代算法能获得较好的估计性能,迭代对于提高算法的性能具有很大的作用,在高信噪比下性能明显优于LS算法。

图2 IFD-SAGE算法的均方误差曲线图
图3给出了在不同最大迭代次数情况下,本文所提改进的FD-SAGE算法误比特率的性能差异。从仿真结果可知,最大迭代次数为5的IFD-SAGE信道算法优于最大迭代次数为1和3的情况。其中最大迭代次数为3的优于最大迭代次数为1的约0.5 dB,但最大迭代次数为5的比最大迭代次数为3的性能没有明显增加。其主要原因是由于信道估计误差会随着算法迭代次数逐次积累,最终导致误比特率升高。同时,最大迭代次数为3时已很接近理想信道估计下的最大似然信号检测算法性能,可以看出本文所提算法能较好地追踪信道的变化,且收敛速度较快。

图3 不同最大迭代次数下IFD-SAGE算法的误比特率曲线图
图4给出了信号检测采用最大似然检测算法在设定的仿真参数条件下,理想信道估计,基于LS信道估计,迭代次数为3的FD-SAGE信道估计,以及迭代次数为3的IFD-SAGE信道估计随信噪比变化的误比特率性能曲线。仿真结果表明:信号检测采用ML算法在相同迭代次数的情况下,IFD-SAGE算法的性能优于FD-SAGE算法,且有了很大程度的改善。在相同误比特率情况下,基于ML检测算法的本文算法性能优于传统的基于ML检测的LS信道估计算法,与基于最大似然检测的理想信道性能相接近,仅相差0.5 dB左右。

图4 ML检测的信道估计算法性能比较
5 结束语
针对衰落信道下MIMO-OFDM系统的信道估计问题,提出了一种改进的FD-SAGE迭代信道估计算法。本文算法充分利用了信道参数的不确定性,通过多次迭代来逼近其真实值,从而提高了信道估计的准确性。通过理论分析和仿真结果表明所提算法具有两个优点:一是本文在SAGE算法迭代的基础上,利用修正公式改善了FD-SAGE算法在高信噪比下的地板效应现象,这样既没有增加算法设计的复杂度又可以减少传统算法带来的系统误差;二是利用在SAGE算法的M步(最大值步)操作中引入ML算法,提高了算法的估计性能,但算法复杂度也有所提高。仿真结果表明,基于ML检测算法的IFD-SAGE算法其性能接近于理想信道估计条件下的最大似然信号检测算法,信噪比仅损失0.5 dB。
[1]Katariya A,Yadav A,Jain N,et al.BER performance criteria based on standard IEEE 802.11a for OFDM in multipath fading environments[C]//Proceedings of the International Conference on Computational Intelligence and Communication Networks,2011:238-241.
[2]Yang H W.A road to future broadband wireless access:MIMOOFDM-based air interface[J].IEEE Communications Magazine,2005,43(1):53-60.
[3]Gao F F,Cui T,Nallanathan A.On channel estimation and optimal training design for amplify and forward relay networks[J].IEEETransactionsonWirelessCommunications,2008,5(7):1907-1916.
[4]Piechocki R J,Nix A R,McGeehan J P,et al.Joint blind and semi-blind detection and channel estimation for space-time trellis coded modulation over fast faded channels[J].IEE Proceedings Communications,2003,150(6):419-426.
[5]Tu C C,Champagne B.Subspace-based blind channel estimation for MIMO-OFDM systems with reduced time averaging[J]. IEEE Transactions on Vehicular Technology,2010,59(3):1539-1544.
[6]Hao J,Yang L.Semi-blind channel estimation of MIMO-OFDM systems based on RBF network[C]//Proceedings of the IET International Communication Conference on Wireless Mobile and Computing,2011:187-191.
[7]Huang L,Bergmans J W M,Willems F M J.Low-complexity LMMSE-based MIMO-OFDM channel estimation via angledomain processing[J].IEEE Transactions on Signal Processing,2007,55(12):5668-5680.
[8]Liu H Y,Yen R Y.Effective adaptive iteration algorithm for frequency tracking and channel estimation in OFDM systems[J].IEEE Transactions on Vehicular Technology,2010,59(4):2093-2097.
[9]Zhang Y,Khalighi M A,Bourennane S.EM-based channel estimation for cooperative relay networks[C]//Proceedings of the11thInternationalConferenceonTelecommunications Proceedings,2011:279-286.
[10]Obradovic D,Szabo A,Mandic D P,et al.Novel EM-based methodforchannelestimationandsignaldetectionin MIMO-OFDM systems[C]//Proceedings of the the International Conference on Computer as a Tool,2005:1795-1798.
[11]Ylioinas J,Raghavendra M R,Juntti M J.Avoiding matrix inversion in DD SAGE channel estimation in MIMO-OFDM with M-QAM[C]//Proceedings of the IEEE 70th Vehicular Technology Conference,2009:1-5.
[12]Shutin D,Fleury B H.Sparse variational Bayesian SAGE algorithm with application to the estimation of multipath wireless channels[J].IEEE Transactions on Signal Processing,2011,59(8):3609-3623.
[13]Frenkel L,Feder M.Recursive Expectation-Maximization(EM)algorithms for time-varying parameters with applications to multipletargettracking[J].IEEETransactionsonSignal Processing,1999,47(2):306-320.
[14]Lisheng F,Fukawa K,Suzuki H.ML detection of MIMOOFDMsignalsinselectedspatial-temporalsubspacefor prewhiteningwithrecursiveeigenvaluedecompositionin mobileinterferenceenvironments[C]//Proceedingsofthe IEEE 65th Vehicular Technology Conference,2007:2114-2118.
[15]Barhumi I,Leus G G,Moonen M S.Optimal training design for MIMO OFDM systems in mobile wireless channels[J]. IEEE Transactions on Signal Processing,2003,51(6):1615-1624.
GAO Jingpeng,ZHAO Danfeng,ZHOU Xiangchao,FU Fang
College of Information and Communication Engineering,Harbin Engineering University,Harbin 150001,China
Aiming at the poor performance of Frequency Domain Space-Alternating Generalized Expectation-Maximization(FD-SAGE)algorithm in channel estimation and the slow convergence speed in the MIMO-OFDM system,this paper presents an improved FD-SAGE channel estimate algorithm.On the basis of FD-SAGE algorithm,a modified SAGE algorithm is derived through decomposing and analyzing the potential and incomplete data of SAGE algorithm.Meanwhile,the maximum likelihood algorithm is introduced in the process of refreshing data information in SAGE algorithm,and then the reliability of system is improved.The theoretical analysis and simulation results show that this algorithm can better track the channel change and acquire a faster convergence speed,just in cost of a slight system complexity.The performance is better than the traditional Least Square(LS)algorithm.Comparing with the ideal channel estimation under the maximum likelihood algorithm in signal detection,the new proposed algorithm has only a loss of 0.5 dB with the same bit error rate.
MIMO-OFDM system;SAGE algorithm;improved FD-SAGE algorithm;channel estimation
针对MIMO-OFDM系统中频域的空间交替广义期望最大化(FD-SAGE)算法估计信道性能较差以及收敛速度慢的问题,提出了一种改进的FD-SAGE信道估计算法。该算法在FD-SAGE算法的基础上,通过对SAGE算法的潜在数据和不完全数据进行分解分析推导出一种修正的SAGE算法,同时在SAGE的更新数据信息时引入最大似然算法,进而提高系统的可靠性。理论研究和仿真结果表明,该算法以牺牲少量复杂度为代价,能较好地追踪信道变化且收敛速度较快,其性能优于传统的LS算法,信号检测采用最大似然算法时,在相同误比特率情况下与理想信道估计仅相差0.5 dB。
MIMO-OFDM系统;SAGE算法;改进的FD-SAGE算法;信道估计
A
TN92
10.3778/j.issn.1002-8331.1301-0076
GAO Jingpeng,ZHAO Danfeng,ZHOU Xiangchao,et al.Improved FD-SAGE channel estimation algorithm for MIMOOFDM system.Computer Engineering and Applications,2013,49(13):1-4.
国家部委预研基金(No.xxxx7010102);中央高校基本科研业务专项基金(No.HEUCF100814)。
高敬鹏(1980—),男,博士研究生,讲师,主要研究领域为信道估计和检测算法,高效信道编码与调制;赵旦峰(1961—),男,博士,教授,主要研究领域为现代通信系统,通信信号处理,高性能编码与调制技术;周相超(1987—),男,博士研究生,主要研究领域为现代通信系统,高性能编码与调制技术;付芳(1985—),女,博士研究生,主要研究领域为现代通信系统,高性能编码与调制技术。E-mail:gjpmcu@126.com
2013-01-10
2013-03-22
1002-8331(2013)13-0001-04
CNKI出版日期:2013-03-29http://www.cnki.net/kcms/detail/11.2127.TP.20130329.1701.023.html

