基于扩展OWA算子的数据信息聚合方法研究

韦纯福，牛义锋

河南理工大学 数学与信息科学学院，河南 焦作 454000

基于扩展OWA算子的数据信息聚合方法研究

韦纯福，牛义锋

河南理工大学 数学与信息科学学院，河南 焦作 454000

1 引言

随着信息技术的飞速发展，需要处理的数据信息越来越多，怎样在大量数据信息中提取出有用的信息，并科学合理地聚合得出最终的结论，逐渐成为人们研究的热点之一。国内外研究人员对聚合算子进行了大量的研究并且取得了卓越的研究成果，Yager[1]在1988年提出了有序加权平均（Ordered Weighted Averaging，OWA）算子，它是一种只考虑数据信息所处位置权重的聚合算子，介于最小算子与最大算子之间的加权平均算子。这种聚合算子介于两种极端之间：一种极端是“与（and）”算子，即所有的情况都被满足；另一种极端是“或（or）”算子，即只要其中一种情况被满足即可。因此OWA算子又被称作“or and”算子。文献[2-4]提出了序加权几何平均（OWGA）算子且论述了其基本性质，其中，文献[4]对OWGA和OWA这两个算子之间的关系进行了详细论述。由于OWA算子与OWGA算子能够有效地聚合不确定的和模糊的数据信息，目前已被广泛运用于管理与决策、专家知识系统[5-7]、模糊控制[8-9]、煤矿安全评价[10-11]和多属性决策[12-14]等方面。

然而，无论是OWA算子还是OWGA算子，在数据信息的聚合过程中仅仅考虑了聚合数据信息所处聚合位置的重要度，而没有考虑数据信息本身的重要度。针对上述聚合算子在数据信息聚合过程中的不足，本文给出了一个扩展的有序加权几何平均聚合算子，并且证明了该扩展聚合算子一些基本性质；基于该扩展的聚合算子，给出了数据信息聚合的一般步骤，该聚合方法不但考虑了指标本身的重要度，而且考虑了指标值在聚合过程中的重要度。通过算例分析验证了该数据聚合方法的有效性。

2 基本定义与相关定理

2.1 OWA算子

定义1.1[1]设OWA：Rn→R，如果满足，其中w=(w1，w2，…，wn)T是与OWA相关联的n维加权向量，且wi∈[0，1]，式中bj是 (a1，a2，…，an)中第j个最大元素，则称函数OWA为n维有序加权平均算子。

Yager教授给出了一种计算权重向量w的方法，w=(w1，w2，…，wn)T可由下面公式确定：

式中，Q为模糊语义量化算子，由下式计算：

式中，α，β，γ∈[0，1]。模糊语义量词Q(r)对应的参数(α，β)值可以有不同的确定方法，通常采取“大多数”、“至少一半”和“尽可能多”这三种指导原则，参数(α，β)依次选取（0.3，0.8），（0，0.5），（0.5，1）。

2.2 OWGA算子

上面这两种聚合算子的共同特点是：首先对数据ai(i∈N)按照由大到小的次序进行排序，然后结合位置权重信息聚合，而且ai与wi并无任何联系，wi仅与聚合过程中其所处的位置i有关系，没有考虑数据信息本身的权重。

3 扩展的OWGA算子

针对OWA算子与OWGA算子在聚合过程中的这种不足，本文对有序加权几何平均算子进行了扩展并且给出了IOWGA算子，详细研究了它的性质，并给出了该算子聚合数据信息的一般步骤，然后进行了算例分析。

下面是本文给出的扩展的有序加权几何平均聚合（IOWGA）算子的定义与性质证明。令M={1，2，…，m}，N={1，2，…，n}。

由定义可知，IOWGA聚合算子不但考虑了聚合信息所处位置的权重，而且考虑聚合信息本身的权重；该算子更能够科学、全面地反映实际情况。在下面的性质证明中，为了表示的方便，设f是一个IOWGA算子。

性质3.1IOWGA聚合算子具有单调性。设(a1，a2，…，an)和是任意的数据向量，cj是数据rϖiai(i∈N)中第j个最大的元素，是数据中第j个最大的元素，若任意给定的j，有cj≥，则下式成立

4 基于IOWGA算子的数据信息聚合方法

以下给出了多属性决策过程中使用IOWGA算子进行数据信息聚合的一般步骤：

步骤1设X={x1,x2,…，xm}为一组方案，U={u1,u2,…，un}为属性集合，权重信息均未知。针对方案xi，按照属性uj对其评价，得到xi关于uj的属性值记为aij，从而构成决策矩阵A=(aij)m×n。属性的类型通常有成本型、固定型、效益型等。为了克服不同的物理量纲对决策结果的影响，信息聚合之前需要对决策矩阵A归一化处理。A经过规范化处理后的矩阵记做R=(rij)m×n。

步骤2求解属性值自身的权重向量利用表1中的0.1～0.9标度语言值对属性集中的值进行两两比较，构造出模糊互补判断矩阵P=(pij)n×n，将其列向量代入互补判断矩阵的优先权重公式（3）[15]，可以得到如下属性权重向量：

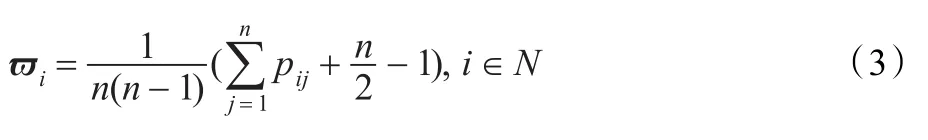
表1 0.1～0.9标度值

表1中，0.2，0.4，0.6，0.8可以取0.1～0.9相邻的判断中值。

步骤3求解每个方案xi(i∈N)的综合属性值zi(i∈N)。具体方法如下：

（1）利用公式（1）与（2）先求得与IOWGA相关联的权重向量

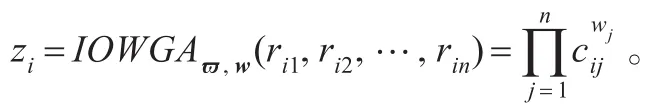
步骤4对综合值zi排序，选出所需方案。

5 算例分析

以某区域变电所选址过程的数据信息的聚合为例，选取与选址相关的覆盖范围Id1，基建投资Id2，运输成本Id3，不稳定费用Id4和预期效益Id5等初步论证方案的5个指标，构成选址方案评价的指标体系，并采用本文给出的方法，确定最优选址方案。下面以某个变电所5个选址方案(Xi，i=1，2，…，5)为例，按照经济效益的优劣对各个方案进行排序，表2列出了各项参数指标值。

采用上面给出的算法进行求解，步骤如下：

步骤1由决策信息表2建立决策矩阵A=(aij)5×5，将A规范化，得到规范化矩阵：

注：这里预期效益u5与覆盖范围u1是效益型指标，不稳定费用u4、运输成本u3和基建投资u2是成本型指标。

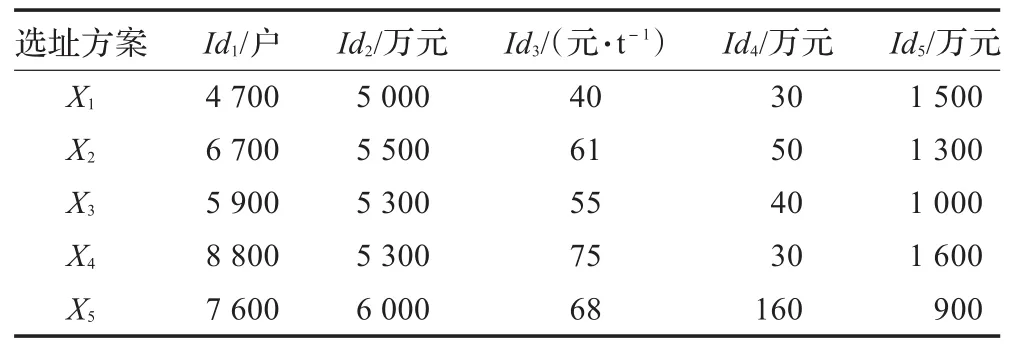
表2 变电所设计方案的参数指标

步骤2决策者根据0.1～0.9互补语言值标度对集合U={u1，u2，…，un}中的属性值做两两比较，并得到如下互补判断矩阵：

利用公式（3），求得属性的权重向量ϖ=(0.225，0.2，0.2，0.15，0.225)T。

步骤3利用公式（1）与公式（2）先求得与IOWGA关联的权重向量w=(0，0.2，0.4，0.4，0)T。

注：这里参数(α，β)选择(0.3，0.8)，即满足“大多数”的指导原则。

通过归一化处理矩阵R=(rij)m×n，并且结合IOWGA算子计算出每个方案Xi(i∈N)的综合属性值zi(i∈N)；平衡因子r=5。由此可求得：

步骤4依次对各方案的综合值进行排序：z1≻z4≻z2≻z3≻z5，故最优选址方案为X1。

现将上面提出的数据信息聚合模型中的聚合算子依次替换为OWA算子与OWGA算子后，再对该算例进行决策分析。

采用OWA算子时：

依次对各方案的综合值进行排序：z1=z4≻z2≻z3≻z5。

在上述算例的数据信息聚合过程中，发现3个算子的聚合结果基本相同（见表3，方案1和方案4除外），使用OWA算子与OWGA算子聚合信息时，方案1和方案4有相同的聚合结果，并列排在第一位；采用本文提出的IOWGA算子时，方案1的聚合结果略大于方案4的聚合结果，此时方案1排在第一位，方案4排在第二位。究其原因，可以发现方案1的评价集合{0.534，1，1，1，0.938}与方案4的评价集合{1，0.938，0.534，1，1}相同，在聚合的过程中，有相同的排序结果，即{1，1，1，0.938，0.534}，所以OWA和OWGA的聚合结果也相同，即z1=z4；当采用ILOWA算子聚合时，评价集合中的元素依次与本身对应的权值相乘后构成了两个新集合，新集合为两个不同的集合，从而新集合中的元素从大到小的排序结果也不相同，因此采用ILOWA算子可以区分出方案1和方案4的优劣。

表3 不同聚合算子聚合结果比较

6 结论

在数据信息聚合的过程中经常会用到聚合算子，本文给出了一种扩展的OWA算子，并且证明了其具有单调性、幂等性、置换不变性等基本性质；通过一个算例验证了该聚合算子不但考虑了数据信息所处位置的权重，而且考虑了各个数据信息自身的权重。今后，将继续研究用于聚合模糊信息和语言值的聚合算子。

[1]Yager R R.On ordered weighted averaging aggregation operators in multi-criteria decision making[J].IEEE Transactions on Systems，Man and Cybernetics，1988，l8：183-190.

[2]Chiclana F，Herllera F.Integrating multiplicative preference relations in a multipurpose decision-making model based on fuzzy preference relations[J].Fuzzy Sets and Systems，2001，122：277-29l.

[3]Herrera F，Herrera-Viedma E，Chiclana F.Multiperson decision making based on multiplicative preference relations[J].European Journal of Operational Research，2001，129：372-385.

[4]Xu Z S，Da Q L.The ordered weighted geometric averaging operators[J].International Journal of Intelligent Systems，2002，17：709-716.

[5]Le C A，Huynh V N，Dam H C.Combining classifier based on OWA operators with an application to word sense disambiguation[J].Proceedings of SPIE，2006，61：512-521.

[6]Xu Z S.Induced uncertain linguistic OWA operators applied to group decision making[J].Information Fusion，2006，7：231-238.

[7]Pei Z，Xu Y.Lattice implication algebra model of linguistic variable truth and its information[J].Applied Computational Intelligence：World Scientific，2004，32：93-98.

[8]孙晓玲，王宁.基于OWA算子的区间值加权模糊推理[J].计算机工程与应用，2012，48（10）：156-159.

[9]杨霁琳，周玉华，秦克云.不完备信息系统中属性的重要度及约简方法[J].计算机工程与应用，2010，46（1）：99-102.

[10]Wei C F，Pei Z，Li H M.An induced OWA operator in coal mine safety evaluation[J].Journal of Computer and System Sciences，2012，78：997-1005.

[11]Wei C F，Yuan R F.A decision-making method based on linguistic aggregation operator for coal mine safety evaluation[C]// Proceedings of the IEEE International Conference on Intelligent Systems and Knowledge Engineering，Hangzhou，China，2010：17-20.

[12]Xu Z S.A note on linguistic hybrid arithmetic averaging operator in multiple attribute group decision making with linguisticinformation[J].GroupDecisionandNegotiation，2006，15：593-604.

[13]Xu Z S.A method based on linguistic aggregation operators for group decision making with linguistic preference relations[J].Information Sciences，2004，166：19-30.

[14]刘家学，刘耀武.带有方案偏好信息的多指标决策法[J].系统工程与电子技术，1999，21（1）：47-50.

[15]Xu Z S.Algorithm for priorities of fuzzy complementary judgement matrics[J].Journal of Systems Engineering，2001，16：93-96.

WEI Chunfu,NIU Yifeng

School of Mathematics and Information Science,Henan Polytechnic University,Jiaozuo,Henan 454000,China

The Ordered Weighted Aggregation（OWA）operator only considers the ordered position of the given argument and few considers the given argument itself in the aggregation of data information.An induced Ordered Weighted Geometric Averaging（IOWGA）operator is presented,which not only considers the ordered position of the given argument but also consider the given argument itself,and some properties are proved.Then aggregation method of decision information based on the induced aggregation operator is scientific and reasonable by theoretical analysis.At last,the method is proved that can more scientifically reflect the real situation by comparative analysis with the common aggregation operators.

weight;attribute value;data information;aggregation operator;Ordered Weighted Aggregation（OWA）

在数据信息聚合的过程中通常会用到有序加权平均聚合算子，然而有序加权平均聚合算子只是考虑了数据信息所处聚合位置的重要度，却很少考虑数据本身的重要度。针对这种缺点和不足，提出了一种扩展的有序加权几何平均聚合算子，证明了该扩展聚合算子的一些基本性质定理；从理论上分析了该扩展聚合算子的科学性和合理性；通过一个算例的对比分析，证实了该扩展的聚合算子在数据信息聚合时更能真实地反映实际情况。

权重；属性值；数据信息；聚合算子；OWA算子

A

TP18；TP273

10.3778/j.issn.1002-8331.1301-0241

WEI Chunfu,NIU Yifeng.Research on data information aggregation method based on induced OWA operator.Computer Engineering and Applications,2013,49（13）：13-16.

国家自然科学基金（No.11226319，No.11226254，No.51274086）。

韦纯福（1979—），男，博士生，讲师，研究领域：智能信息处理，模糊集合理论；牛义锋（1981—），男，博士生，讲师，研究领域：系统可靠性、集成、分析。E-mail：weichunfu@hpu.edu.cn

2013-01-22

2013-04-07

1002-8331（2013）13-0013-04

CNKI出版日期：2013-04-11http://www.cnki.net/kcms/detail/11.2127.TP.20130411.1555.005.html