广义标准自动机及其商自动机

徐　慧，田　径，金英姬

(1.空军工程大学 基础部, 陕西 西安　710051;2.西安外国语大学 金融学院, 陕西 西安　710128；3.西藏民族大学 教育学院，陕西 咸阳　712082)

1936年英国数学家Turing提出一种抽象的自动机—图灵机,用来定义可计算函数类,自此开创了自动机理论的抽象研究[1]。二十世纪五六十年代,由于计算机、通信和人工智能的兴起,自动机理论得到了迅速发展。自动机不仅成为计算机科学的理论基础,而且在信息科学、生命科学、管理学、控制学等众多学科领域有着广泛应用[2-8]。

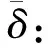
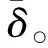
设自动机A=(Q,Σ,δ), 任取q∈Q, 令〈q〉表示集合{δ(q,u) |u∈Σ*}。 称自动机A(q)=(〈q〉,Σ,δ〈q〉×Σ)为由q生成的子自动机[5], 其中δ〈q〉×Σ表示δ在〈q〉×Σ上的限制。 进一步,若A=A(q), 则称q为A的生成元[10]。A的所有生成元构成的集合用Gen(A) 表示,称之为生成元集。 若Gen(A)≠∅, 则称A是循环自动机[10]。

设A=(Q,Σ,δ)是循环自动机, 在Q上定义二元关系LE如下:

LE{(p,q)∈Q×Q| (∃s∈Gen(A))p,q∈Os}，

其中

Os={f(s) |f∈E(A)}。

若LE是Q上的等价关系,则称A是标准自动机[11]。

文献[11-12] 中证明了循环交换异步自动机和强连通自动机是标准自动机，同时将强连通自动机的表示推广到标准自动机。在此基础上,本文将介绍一类非循环自动机,即广义标准自动机。我们将给出广义标准自动机的几个刻画。同时,讨论广义标准自动机的商自动机的循环性。

1　预备知识

设A=(Q,Σ,δ) 和B=(Q′,Σ,γ) 是自动机,f是从Q到Q′的映射。若对于任意的q∈Q和任意的x∈Σ有f(δ(q,x))=γ(f(q),x)成立,则称f是A到B的同态[10]。 若同态f是双射,则称f为同构[10]。 自动机A到其自身的同态和同构分别称为自同态和自同构。我们用E(A)和G(A)分别表示A的自同态和自同构的全体。 在通常意义的映射合成运算下,E(A)和G(A)分别构成幺半群和群,分别称为自同态幺半群和自同构群[10]

设A=(Q,Σ,δ)，ρ是状态集Q上的等价关系。 若对任意的p,q∈Q和任意的x∈Σ，有

(p,q)∈ρ⟹(δ(p,x),δ(q,x))∈ρ,

则称ρ是自动机A上的同余[10]。按照泛代数中的记号,我们将q所在的ρ类记为ρq,即

ρq={p∈Q| (p,q)∈ρ}。

设A=(Q,Σ,δ),ρ是A上的同余。 记Q/ρ={ρq|q∈Q}, 对任意的ρq∈Q/ρ和任意的x∈Σ定义δρ(ρq,x)=ρδ(q,x)。 称自动机A/ρ=(Q/ρ,Σ,δρ) 为A关于ρ的商自动机。

若A=(Q,Σ,δ)是非循环自动机,则Gen(A)=∅。 若存在S⊆Q, 使得Q=∪s∈S〈s〉, 即对任意的q∈Q, 存在s∈S和u∈Σ*，使得q=δ(s,u), 则称S是A的生成元集[13]。 进一步, 如果对于任意的s,t∈S有 〈s〉≠〈t〉, 那么称S是A的极小生成元集[13]

设A=(Q,Σ,δ),S={s1,s2,…,sn}是A的极小生成元集。如果对任意的f∈E(A)和任意的i∈{1,2,…,n}有f(si)∈〈si〉, 那么我们就称A是广义正规自动机。

文中未定义的概念和符号请参考文献[10,14]。

2　广义标准自动机的刻画

设A=(Q,Σ,δ)是广义正规自动机, 在Q上定义二元关系L如下:

其中Oi={f(si) |f∈E(A)}, [n]={1,2,…,n}。

容易验证，当A是循环自动机时, L=LE。

设A=(Q,Σ,δ)是广义正规自动机, 若L是Q上的等价关系, 则称A是广义标准自动机。

文献 [15]给出了L是等价关系的一个充分必要条件，结论如下。

引理1[15]设A=(Q,Σ,δ) 是广义正规自动机,S={s1,s2,…,sn} 是A的极小生成元集, 则A是广义标准自动机当且仅当如下条件成立:

1)任意q∈Q存在i∈[n],f∈E(A)，使得q=f(si);

2)若f(si)=f(sj), 则i=j。

设A=(Q,Σ,δ)是广义标准自动机, 任取i∈[n], 记Li={q∈Q| (q,si)∈L}。 根据L的定义可知,Li⊆Oi。 反之, 设q∈Oi, 则 (q,si)∈L。 这是因为si=I(si), 其中I是Q上的恒等映射,从而q∈Li。 这样, 我们得到了如下结论。

命题1设A=(Q,Σ,δ)是广义标准自动机, 则对任意的i∈[n]有Li=Oi。

在命题1的基础上,立即可以得出广义标准自动机的一个刻画。

定理1设A=(Q,Σ,δ) 是广义正规自动机, 则A是广义标准自动机当且仅当对任意的q∈Q存在唯一的i∈[n] ，使得q∈Oi。

下面,我们证明L是广义标准自动机上的同余关系。

命题2若A=(Q,Σ,δ) 是广义标准自动机, 则L是A上的同余关系。

证明设A=(Q,Σ,δ), 任取q,p∈Q。 若(q,p)∈L, 则存在i∈[n],f,h∈E(A) 使得q=f(si),p=h(si)。 任取u∈Σ*,根据引理1可知,存在j∈[n],g∈E(A) 使得δ(si,u)=g(sj)。 因此

δ(q,u)=δ(f(si),u)=f(δ(si,u))=(fg)(sj),

δ(p,u)=δ(h(si),u)=h(δ(si,u))=(hg)(sj),

从而(δ(q,u),δ(p,u))∈L。根据u的任意性可知,L是A上的同余。

3　商自动机的循环性

设S={s1,s2,…,sn} 是A的极小生成元集。 显然, 当n=1时，A是循环自动机。 此时，A/L也是循环的。 若n>1, 则A/L未必是循环自动机。下面我们给出n=2 时A/L是循环自动机的一个充分必要条件。

引理2设A=(Q,Σ,δ),S={s1,s2}是A的极小生成元集。 若A是广义正规自动机,则〈s1〉∩〈s2〉≠∅。

证明采用反证法。 假设〈s1〉∩〈s2〉=∅,则对任意q∈Q,v∈Σ*有,q∈〈si〉 与δ(q,v)∈〈si〉是等价的。定义映射f:Q→Q如下:

f(s1)=s2,f(s2)=s2,

(∀u∈Σ*)f(δ(s1,u))=δ(s2,u),

(∀u∈Σ*)f(δ(s2,u))=δ(s2,u)。

可以证明f∈E(A)。由于f(s1)∈〈s2〉, 这与A是广义正规自动机矛盾。 因此假设错误, 所以〈s1〉∩〈s2〉≠∅。

引理3设A=(Q,Σ,δ) 是广义标准自动机,S={s1,s2} 是A的极小生成元集, 则A/L是循环自动机当且仅当〈s1〉∩〈s2〉≠∅。

证明(必要性)由于A是广义正规自动机, 且|S|=2, 所以 |Q/L|=2。 若A/L是循环自动机, 则Gen(A/L)≠∅。 不妨设L1∈Gen(A/L), 则存在u∈Σ*使得δL(L1,u)=L2, 即Lδ(s1,u)=L2。 从而δ(s1,u)∈L2。 由于A是广义正规自动机,L2⊆〈s2〉, 因此,δ(s1,u)∈〈s2〉。 故〈s1〉∩〈s2〉≠∅。

(充分性)若〈s1〉∩〈s2〉≠∅, 则存在s∈〈s1〉∩〈s2〉。 由于A是广义标准自动机, 根据引理1可知,存在i∈{1,2}使得s∈Oi。 不妨假设s∈O1, 那么存在f∈E(A) 使得s=f(s1)。 另一方面, 由于s∈〈s2〉, 存在u∈Σ*使得s=δ(s2,u)。 因此s=f(s1)=δ(s2,u)。 从而L1=Ls=Lδ(s2,u)=δL(Ls2,u)。 故L2∈Gen(A/L), 所以A/L是循环自动机。

注意到广义标准自动机是广义正规自动机, 根据上述两个引理可得

命题3设A=(Q,Σ,δ)是广义标准自动机。若S={s1,s2} 是A的极小生成元集 (即极小生成元集中有两个元素),则A/L是循环自动机。

命题4设A=(Q,Σ,δ) 是广义标准自动机,S={s1,s2,…,sn} 是A的极小生成元集 (n≥3), 若A/L是循环的, 则存在i∈[n], 使得对任意的j∈[n](j≠i) 有〈s1〉∩〈s2〉≠∅, 并且Li∈Gen(A/L)。

证明若A/L是循环自动机, 则存在i∈[n] 使得Li∈Gen(A/L)。 从而对任意的j∈[n]存在uj∈Σ*使得δL(Li,uj)=Lj。 即Lδ(si,uj)=Lj。 故δ(si,uj)∈Lj⊆〈sj〉。 因此〈s1〉∩〈s2〉≠∅。

命题5设A=(Q,Σ,δ)是广义标准自动机,S={s1,s2,…,sn}是A的极小生成元集。 若对任意i,j∈[n] (i≠j) 有〈s1〉∩〈s2〉≠∅, 则A/L是循环自动机。

证明任取i,j∈[n], 若〈s1〉∩〈s2〉≠∅, 则存在s∈〈s1〉∩〈s2〉。 不妨设s∈Oi, 那么存在f∈E(A) 使得s=f(si)。 另一方面,由于s∈〈sj〉, 存在u∈Σ*使得δ(sj,u)=s。 因此,Li=Ls=Lδ(sj,u)=δL(Lsj,u)。 即Lj可以到达Li。 根据i,j的任意性可知,A/L是循环自动机。

参考文献：

[1]TURING A M. On computable number, with an application to the Entscheidungs problem[J].Proceedings of the London Mathematical Society, 1936,2(42):230-265.

[2]RABIN M O, SCOTT D. Finite automata and their decision problems [J]. IBM Journal of Research and Development, 1959, 3 (2): 114-125.

[3]SCHÜTZENBERGER M P. On the definition of a family of automata [J]. Information and Control, 1961, 4(2): 245-270.

[4]MOHRI M. Finite-state transducers in language and speech processing [J].Computational linguistics, 1997, 23(2): 269-311.

[5]RAMASUBRAMANIAN S V, KRITHIVASAN K. Finite automata digital images [J].International Journal of Pattern Recognition and Artificial Intelligence, 2000, 14:501-524.

[6]ANDERSON J A. Automata Theory with Modern Applications [M].Cambridge：Cambridge University Press, 2006.

[7]GOPALAKRISHNAN G. Computation Engineering: Applied Automata Theory and Logic[M]. New York: Springer, 2006.

[8]KOHAVI Z, JHA N K. Switching and Finite Automata Theory [M].Cambridge：Cambridge University Press, 2010.

[9]FLECK A C. Isomorphism groups of automata [J]. Journal of the Association for Computing Machinery, 1962, 9(4): 469-476.

[10] HOWIE J M. Automata and Languages[M]. Oxford: Clarendon Press, 1991.

[11] TIAN J, ZHAO X Z. Representations of commutative asynchronous automata [J].Journal of Computer and System Sciences, 2012, 78: 504-516.

[12] 田径. 关于自动机代数理论的研究 [D]. 西安: 西北大学, 2012.

[13] BAVEL Z. Structure and transition-preserving functions of finite automata [J].Journal of the Association for Computing Machinery, 1968, 15 (1): 135-158.

[14] ITO M. Algebraic Theory of Automata and Languages [M].Oxford：World Scientific Publishing Co.Pte.Ltd., 2004.

[15] 徐慧, 田径, 冯军庆. 有关本原自动机的研究 [J]. 空军工程大学学报, 2016,17(2):88-90.