零边界条件下二维元胞自动机矩阵可逆性分析

刘碧川，吴秋轩

(杭州电子科技大学自动化研究所，浙江杭州310018)

0 引言

元胞自动机是定义在一个由具有离散、有限状态的元胞组成的元胞空间上，并按照一定局部规则，在离散的时间维上演化的动力学系统。元胞自动机理论自提出以来得到了长足的发展，开始只是对元胞自动机进行了探索性的研究［1］，逐步将建立在矩阵代数中的一维元胞自动机扩展到二维元胞自动机［2］，而后对9邻域结构的二维元胞自动机进行了研究［3］，并且对二维元胞自动机的等效转移矩阵特性进行了初步的分析［4］。本文在其研究基础上对矩阵的可逆性研究进行一些探索，在一定程度上增进了二维元胞自动机的矩阵特性的理论发展。

1 二维元胞自动机

二维元胞自动机的元胞分布在二维网格中，元胞下一时步的状态取决于当前元胞和其相邻元胞的状态。对于 9 相邻元胞结构，第(i，j)个元胞在 t+1 时步的状态 q 可表述为 qi，j(t+1)=f［qi－1，j－1(t)，qi－1，j(t)，qi－1，j+1(t)，qi，j－1(t)，qi，j(t)，qi，j+1(t)，qi+1，j－1(t)，qi+1，j(t)，qi+1，j+1(t)］，其中 f表示局部规则。

元胞自动机中演化规则是定义在空间局部范围内的，因而，在指定规则之前，必须定义一定的邻域规则。以最常用的规则四方网格划分为例，二维元胞自动机的常用的邻域结构主要有Moore型和Von Neumann型，分别如图1(a)、(b)所示。

中心元胞表示当前元胞，周围元胞表示其相邻元胞。Moore型邻域结构由当前元胞和8个相邻元胞组成，Von Neumann型邻域结构由当前元胞和其上下左右共计5个元胞构成。网格中的数字则表示其规则号，如Rule 1表示当前元胞只受其本身的影响，Rule 32则表示当前元胞只受到其左边元胞的影响。图1(a)中这9个规则称为基础规则。若当前元胞受到两个或多个元胞的影响，则规则号表示为几个基础规则号的代数和(只考虑线性规则)，如常用的Rule 170(128+32+8+2)表示当前元胞受到上下左右4个相邻元胞的影响。

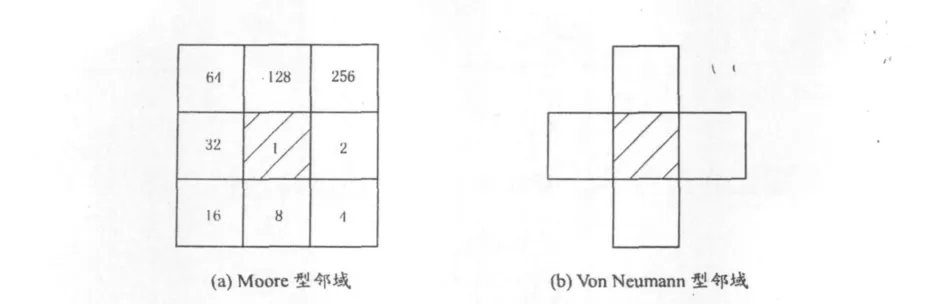
图1 二维元胞自动机邻域结构

2 二维元胞自动机的描述矩阵

二维元胞自动机在任一时步的状态均可用m×n阶位信息矩阵来表示。为便于分析，将转移规则按文献3，5中所述等效为mn×mn阶矩阵M，初始状态中每一行进行转置成Xmn×1，则下一时步状态Ymn×1=MXmn×1。若元胞仅有{0，1}两个状态，但MX会产生不属于这个状态集中的2，3…状态，这是由于实际中当前元胞的状态是由其相邻元胞状态异或得到的，而在数学表达式中却是简单的相加，故准确来讲，下一状态Y=MX mod 2。由此可推得，对于k个有限状态{0，1，2，…，k－1}的元胞自动机，其下一状态Y=MX mod k，其中X为当前状态，M为元胞规则的等效矩阵。

在零边界条件下，二维元胞自动机的等效转移矩阵 M为三对角矩阵，即 M=。其中，D，U，L=0 或 In×n或(T1)n×n或(T2)n×n或 Sn×n或(I+T1)n×n或 (I+T1)n×n或 (I+S)n×n［6］，S=T1+T2，T1和 T2是 两 个 基 础 矩 阵，分 别 为 T1=

转移矩阵M的特性取决于其子矩阵D，U，L的取值。D表示当前元胞受到其同一行元胞的影响的情况，若不受影响，则D=0，反之亦然;U和L分别表示当前元胞受到其下一行元胞和上一行元胞的影响情况［7］。

3 规则矩阵的可逆性

若用 Mi表示第 i号规则，其中 i=1，2，3，…，511，即 M1表示 Rule 1，M2表示 Rule 2，以此类推。由于规则矩阵的线性可加性，且M32=(M2)T，M64=(M4)T，M128=(M8)T，M256=(M16)T则根据文献4中所述，将{M1，M2，M4，M8，M16}做为基础矩阵，其他规则矩阵都可由此5个基础矩阵变换得到，例如 M15=M1+M2+M4+M8，M33=M1+M32=M4+(M2)T。

对5个基础矩阵的块矩阵进行分析，可得M1中D=I，U=L=0;M2中D=T1，U=L=0;M4中U=T1，D=L=0;M8中 U=I，D=L=0;M16中 U=T2，D=L=0。

根据以上分析结果，假设当前元胞的下一时步状态仅与其Moore型邻域的4个对角元胞(即其中非Von Neumann 型邻域)相关，则转移矩阵 M中，U，L=(T1)n×n或(T2)n×n或 Sn×n。可得 M中(或经过初等变换)必有全0行，故M不可逆。由此可得:

定理 若元胞自动机的规则矩阵可逆，则当前元胞的下一时步状态与其Von Neumann型邻域的当前状态相关。

例:2×3维元胞自动机的状态转移矩阵M276=0，其中，S=T1+T2，故|M276|=0，M276不可逆。

4 结束语

本文介绍了二维元胞自动机常见的两种邻域结构，并对Moore型邻域结构更新规则的状态转移矩阵进行了拓展，并对矩阵的可逆性进行了探索性的研究，指出了规则矩阵的可逆性和其Von Neumann型邻域的联系，但二维元胞自动机状态转移矩阵可逆性的研究还没有一个系统的方法，还需要进一步的探究。

［1］ Norman H Packard，Stephen Wolfram.Two-Dimensional Cellular Automata［J］.Journal of Statistical Physics，1985，38(5－6):901－946.

［2］ Chowdhury D R，Gupta IS，Chaudhuri P P.A low cost high capacity associative memory design using cellular automata［J］.IEEE Trans on Computers，1995，44(10):1 260 －1 264.

［3］ Khan A R，Choudhury PP，Dihidar K.VLSIarchitecture of a cellular auto mat a machine［J］.Computers and Mathematics with applications，1997，33(5):79 －94.

［4］ Choudhury P P，Birendra K N，Sudhakar Sahoo，et al.Theory and Applications of Two－ dimensional，Null-boundary，Nine-Neighborhood，Cellular Automata Linear rules［EB/OL］.http://arxiv.org/abs/0804.2346，2008 －04 －15.

［5］ Chattopadhyay P，Choudhury P P，Dihidar K.Characterisation of a Particular Hybrid Transformation of Two-Dimensional Cellular Automata［J］.Computers＆ Mathematics with Applications，1999，38(5－6):207－216.

［6］ Abdul Raouf Khan.Classification of2D Cellular Automata Uniform Group Rules［J］.European Journal of Scientific Research，2011，64(1):51－57.

［7］ Santoso J，Santoso O Slamet，Trilaksono B Riyanto.Matrix characteristics for two dimensional nongroup Cellular Automata［A］.International Conference on Electrical Engineering and Informatics［C］.Bandung，Indonesia，2011:1－4.