基于改进PSO算法的任务分配研究
曾文权,余爱民
广东科学技术职业学院 计算机工程学院,广东 珠海 519090
基于改进PSO算法的任务分配研究
曾文权,余爱民
广东科学技术职业学院 计算机工程学院,广东 珠海 519090
1 引言
虚拟企业是一种企业经营模式,在获得客户订单后,盟主企业首先将订单任务分解和分类为若干个子任务,然后采用招投标或协商等方式为每个子任务选择合适的供应商,该过程即虚拟企业中的任务分配或任务调度。
针对虚拟企业中的任务分配或调度问题,已有研究大多基于多Agent的协商与协作能力,首先建立起任务分配或调度的数学模型,然后采用各种数学方法或智能优化算法进行模型的求解[1-3];或者基于多Agent技术设计和开发任务的分配或调度系统[4-5]。任务的分配与调度是一个NP难题[6],PSO算法由于其具有收敛速度快以及鲁棒性好等优点而得到了广泛应用,如针对多无人作战飞机的协同控制[7-9]、雷达干扰[10]、多机器人系统[11]、网格系统[12]等领域的任务分配与调度。然而,PSO算法存在着易早熟收敛、后期搜索精度与迭代效率不高等缺陷[13-14]。因此,实际应用中,对基于PSO求解任务分配与调度问题大多需要进行改进。改进的方法包括:引入声搜索策略以克服陷入局部最优[15];采用自适应惯性权重提高算法的收敛速度[7];在算法中引入遗传算法中的克隆和变异算子[11];模拟生物免疫系统的特征和机制改进PSO算法[9]基于网格的特性与PSO的混合粒子群的算法[16]等。由于虚拟企业中订单任务的分配是一个多目标优化问题,盟主企业期望以最少的费用、最短的交货期、最高的供应质量和最小的风险等完成订单任务。因此,本文首先建立起订单任务分配的多目标优化决策模型,然后在分析传统PSO算法的基础上对其进行改进,并基于该方法求解任务的分配问题,最后通过实际应用实例和仿真实验来验证该方法的可行性和有效性。
2 任务分配的多目标决策模型
2.1 模型假设
记n个待分配任务记为T={t1,t2,…,ti,…,tn},则模型假设和参数描述为:
(1)任务ti之间相互独立,任务ti的候选供应商集合记为Pi={pi1,pi2,…,pij,…,pimi};
(2)若任务ti分配给了供应商pij,则状态变量uij=1,否则uij=0;
(3)供应商pij申请任务ti的信息中包括完成任务的费用cij、交货期限tij、质量等级qij;
(4)盟主企业对供应商pij的综合信任度为rij;
(5)盟主企业期望以最少的费用(C)、最短的交货期限(T)、最高的质量等级(Q)和最小的风险(R)完成订单任务。
2.2 建立模型
任务分配的目标即为每个ti(i=1,2,…,n)从Pi中选择一个供应商pij(i=1,2,…,n;j=1,2,…,mi),以满足盟主企业的期望。假设盟主企业对供应商的信任度记为TR,则其任务分配的目标函数为:

然而,上述目标在实际中是不可能实现的,针对该目标只能求得一组优化解。在对cij、tij、qij以及trij按Min-Max方法归一化处理后,建立任务分配目标的决策优化模型为:
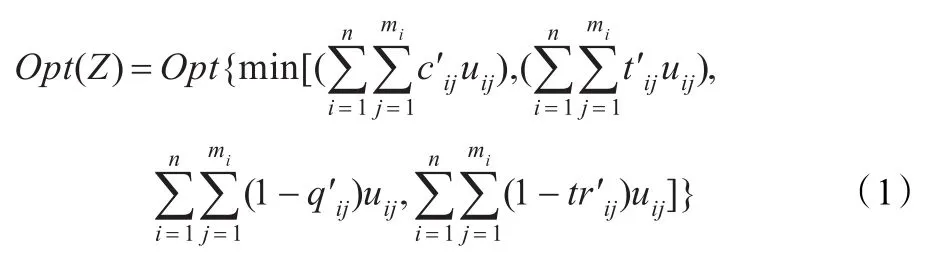
3 PSO算法与改进
3.1 PSO算法
PSO算法模拟鸟群的觅食行为,其基本思想是:粒子(一个候选解)从随机的初始位置以随机的初始速度开始搜索,并记录下搜索过程中单个粒子所经历的最好位置(个体最优解),以及整个粒子群体所经历过的最好位置(全局最优解),一次搜索结束后各个粒子通过个体最优解和全局最优解更新自己的飞行速度和位置,并进行下一轮的搜索,依此直至搜索次数达到设定值,则全局最优解为搜索问题的优化解。

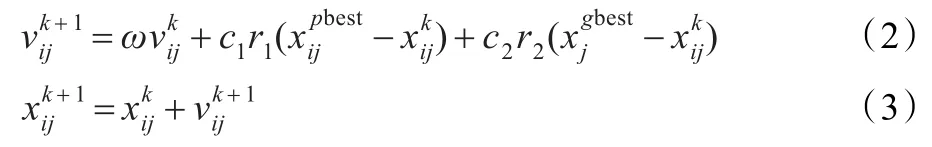
其中ω为速度惯性权重;c1和c2为加速度系数,分别为将粒子推向和的权重;r1和r2为区间[0,1]上的随机数。
3.2 PSO算法的改进
实践证明,PSO算法具有收敛速度快和通用性强的优点,但存在着易早熟收敛,搜索精度不高,以及后期迭代效率不高等缺陷[13-14]。因此,本文从PSO算法参数的调整,并引入遗传算法中的变异操作对其进行改进,在保留其优势的同时克服其不足。
(1)速度惯性权重的调整
速度惯性权重ω取值较大时有利于克服算法陷入局部最优,而取值较小时有利于算法收敛。因此,在算法的起初阶段,由于粒子缺乏对搜索空间的认识且没有足够的参照,ω应取较大值以扩大粒子群的搜索范围,从而提高搜全率;而在算法的收敛阶段,ω应取较小值以尽可能搜索最优解周边的小范围,从而提高搜准率。因此,设定ω的自动调整公式为:

其中ωk为第k(k=2,3,…,T)次搜索时的惯性权重,T为最大搜索次数,ω1为惯性权重的初始值。
(2)c1和c2的调整
c1和c2是分别用于调整个体最优解与全局最优解在粒子搜索过程中所起作用大小的两个参数。对c1和c2的调整策略为:若粒子当前位置的适应度大于粒子群体适应度的平均值,则增大c1且减小c2,以增加粒子沿自身方向飞行的速度,而减少向全局极值方向飞行的速度,反之采用相反策略。
c1和c2的自动调整方式描述为:记第k次搜索时粒子位置的适应度值为,而粒子群体适应度的平均值为,则第k+1次搜索时c1和c2的调整公式如下:
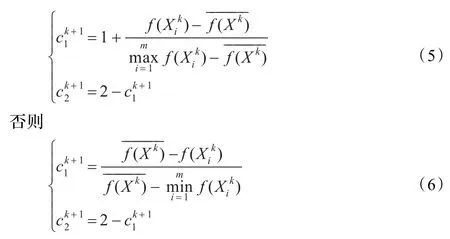
(3)引入变异操作
为了避免粒子群陷入局部最优,在算法中引入遗传算法中的变异操作。若单个粒子的个体最优解连续ξ(变异阈值)次没有更新,则采用两点变异策略对做变异操作。首先,产生[1,n]内的两个随机数na和nb(1≤na≠nb≤n),然后将中位置序号分别为na和nb的两个元素交换位置后作为粒子新的个体最优解。
4 基于改进PSO算法求解任务分配模型
4.1 问题与粒子的映射
针对模型(1),待分配的任务数n即粒子搜索空间的维度,则粒子i的位置为Xi=(xi1,xi2,…,xij,…,xin),xij即为任务tj分配的候选供应商序号,且xij取区间[1,mj]内的整数,mj为申请任务tj的供应商个数;粒子速度vij的取值范围设定为[-(mj-1),(mj-1)]。
由于xij取整数,当采用式(3)更新粒子位置后,若其值在[1,mj]内,则直接取结果的整数部分。否则,若xij>mj,则xij=mj;若xij<1,则xij=1。当按式(4)更新粒子的速度后,若vij>mj-1,则vij=mj-1;若vij<-(mj-1),则vij=-(mj-1)。
4.2 粒子位置适应度值的计算
在计算粒子群中各粒子位置的适应度值时,本文采用TOPSIS[17]方法进行计算。设粒子群的粒子个体数m,则其计算方法描述为:
步骤1根据各粒子的位置Xi,得到粒子群的位置M= (xi1,…,xij,…,xin)m×n。
步骤2根据xij读取出对应的费用信息cij、交货期限tij、质量等级qij和综合信任度trij,则M变形为M′=[(ci1,ti1,qi1,tri1),…,(cij,tij,qij,trij),…,(cin,tin,qin,trin)]m×n。
步骤3针对M′中的(cij,tij,qij,trij),首先对各个分量按列进行归一化处理后,然后计算M′中各行与正理想解和负理想解之间的距离,其计算公式分别为:

步骤4计算出各个粒子的位置适应度值,公式为:

4.3 任务分配模型的求解算法
基于改进的PSO算法求解任务分配模型(1)的算法步骤为:
步骤1设置算法的参数。设粒子群粒子个数为m,最大搜索次数(迭代次数)为T,粒子群惯性权重初始值和最后一次搜索时的值分别为ω1和ωT,设定c1和c2的初始值,以及变异阈值ξ。
步骤2随机生成粒子群的初始位置和初始速度
步骤3计算出粒子群中各个粒子的位置适应度值,进而得到单个粒子的个体最优解和粒子群的全局最优解
步骤4采用式(2)和(3)更新粒子群的速度vij和位置xij,对vij和xij的取值按4.1节的方法进行处理。
步骤5若搜索次数k=T,转步骤7;否则转步骤6。
步骤6对步骤3中连续ξ次未变化过的做变异操作,然后按(4)、(5)和(6)式更新惯性权重,c1和c2,并转步骤3。
步骤7输出步骤3中的,即为模型(1)的最优解,算法结束。
5 应用实例及仿真实验
5.1 应用实例
某面向全球范围从事机械类零部件产品加工定制的虚拟企业,盟主企业将4类待分配任务t1、t2、t3和t4向虚拟企业中的供应商成员企业发布后,针对各个任务,收集到供应商提交的任务申请信息包括费用(万元)、交货期限(天)、质量等级,如表1所示。

表1 各供应商对任务的申请信息
对表1中的信息加上盟主企业对各供应商的信任度值后,按Min-Max方法进行归一化处理后的结果,如表2所示。

表2 归一化后的任务申请信息
按照本文的任务分配求解算法,采用Matlab 7.0提供的PSO算法工具进行求解。求解过程中,设置粒子群粒子的个数m=10,粒子搜索空间的维度n=4,最大搜索次数T=50,初始惯性权重和最后一次搜索的惯性权重分别为ω1=0.9和ωT=0.1,c1和c2的初始值分别设为2,变异阈值ξ=4,求解结果如表3所示。

表3 算法运行结果
对表2中所有的240种任务分配组合分别进行适应度值计算后,其结果与算法的求解结果一致,均表明任务分配序列(2,3,3,3)为最优解。
5.2 仿真实验
为了验证本文方法有效性,任务数分别设为10个、20个、50个、70个和100个,各个任务的候选供应商个数假设都为10个,供应商提交的任务申请信息以及盟主企业对供应商的信任度值取[0,1]上随机数的条件下,分别采用本文的方法和传统PSO算法进行求解。求解时:设定粒子群个数m=50,搜索空间维度为任务的个数,最大迭代次数T=1 000;针对本文改进的PSO算法,设定ω1=0.9,ωT=0.1,c1和c2的初值均为2,ξ=4;PSO算法中ω=0.9,c1=2,c2=2。针对不同任务数的仿真结果分别如图1~图5所示,各任务数与收敛时的搜索次数关系如图6所示。
图1~图5的实验结果表明,本文对PSO算法进行改进后,既提高了传统PSO算法的收敛速度,也克服了其易陷入局部最优解的缺陷。并且从图6可看出,随着求解问题规模的扩大,算法的收敛次数不是呈指数变化,进一步说明本文方法有较好的优化特性。
6 结束语
为了提高PSO算法的收敛速度,尽量避免算法陷入局部最优,通过PSO算法中可调节参数的自动调整,并引入遗传算法中的变异操作,进而设计了基于改进PSO算法求解任务分配多目标优化模型的方法。实验证明该方法既保留了PSO算法易实现和收敛速度快的优点,同时克服了其容易陷入局部最优的缺陷。本文的方法对类似多目标组合优化问题的求解具有一定的参考意义。
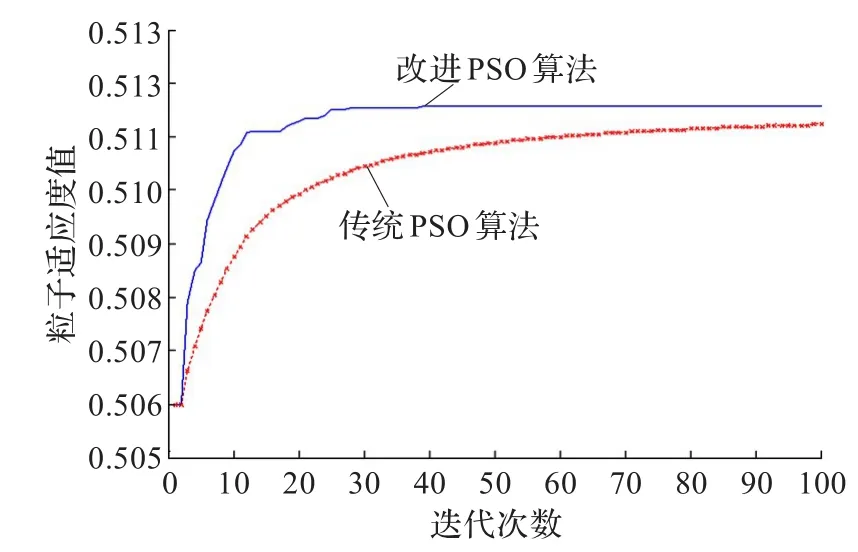
图1 10个任务的实验结果

图2 20个任务的实验结果
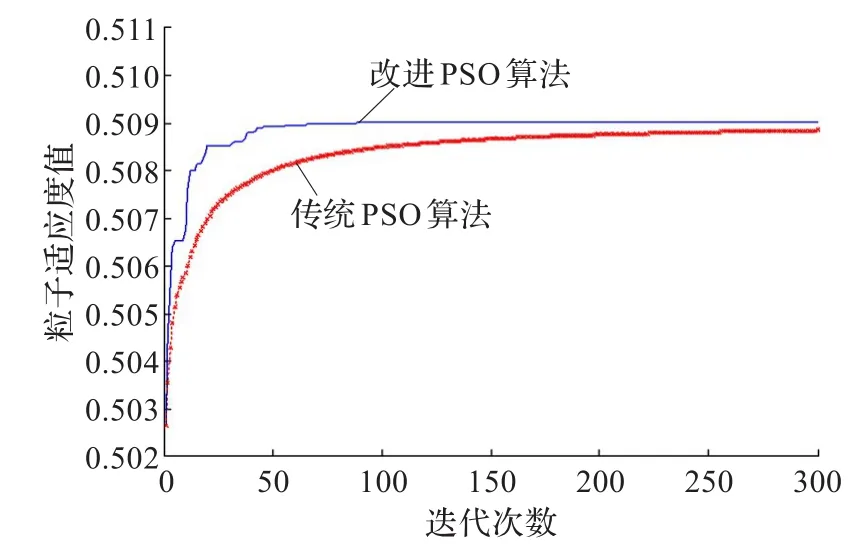
图3 50个任务的实验结果
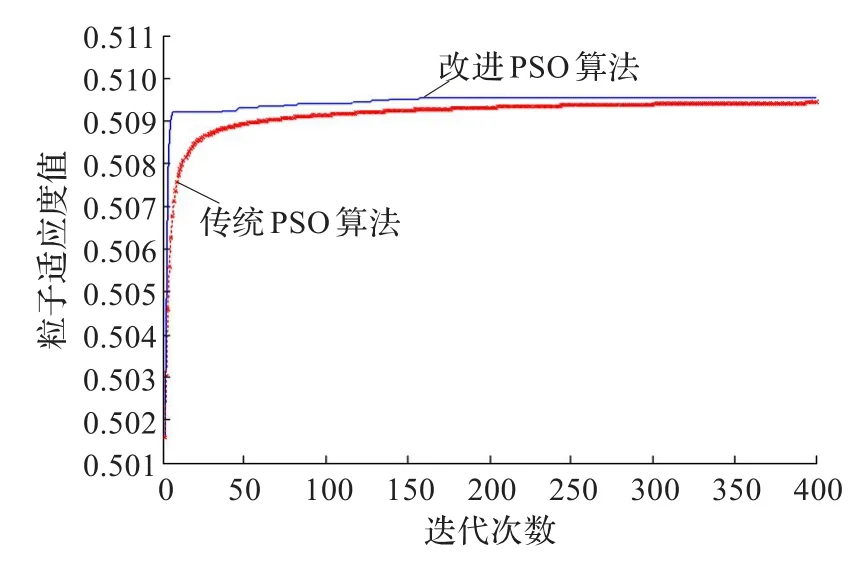
图4 70个任务的实验结果

图5 100个任务的实验结果

图6 任务个数不同时的搜索次数
[1]高阳,周伟.基于多Agent的虚拟企业调度研究与实现[J].中国机械工程,2004,15(11):978-982.
[2]赵强,肖人彬.基于多Agent的虚拟企业任务调度模型[J].控制理论与应用,2009,26(4):459-462.
[3]程方启,王洪飞,叶飞帆.横向虚拟企业订单分配模型研究[J].机电工程,2009,26(4):50-52.
[4]Kyung-Hyun C,Dong-Soo K,Yang-Hoi D.Multi-agent based taskassignmentsystemforvirtualenterprises[J].Robotics and Computer Integrated Manufacturing,2007,23:624-629.
[5]Shen Chenglin.Decision models of task assignment for virtual enterprise based on multi-agent theory[C]//Proceedings International Conference on Management and Service Science,2009.
[6]Lin W,Byrnes C.Control of discrete-time nonlinear system[J]. IEEE Transactions on Automatic Control,1996,41(4):494-510.
[7]杜继永,张凤鸣,杨骥,等.多UCAV协同任务分配模型及粒子群算法求解[J].控制与决策,2012,27(11):1751-1755.
[8]国博,王社伟,陶军.基于改进粒子群算法的多无人机任务分配研究[J].计算机仿真,2009,26(7):62-65.
[9]有伟,王社伟,陶军.基于免疫粒子群算法的多UCAV协同任务分配[J].计算机工程与应用,2010,46(32):224-227.
[10]李俊,郝成民,刘湘伟.改进PSO算法在雷达干扰任务分配中的应用[J].计算机仿真,2008,25(12):27-29.
[11]李济泽.基于粒子群遗传优化算法的多机器人任务分配研究[J].机械与电子,2007(10):45-48.
[12]王成昌,陈闳中,方钰,等.基于混合粒子群算法的网格任务调度[J].计算机科学,2012,39(2):18-21.
[13]Angeline P J.Evolutionary optimization versus particle swarm optimization:philosophyandperformancedifference[C]// Proc of the 7th Annual Conf on Evolutionary Programming,Germany,1998.
[14]刘衍民.粒子群算法的研究及应用[D].济南:山东师范大学,2011.
[15]陈大川,张荣国,黄付亮,等.PSO算法在子任务分配中的应用[J].计算机工程,2011,37(24):183-186.
[16]叶春晓,罗娟.基于网格的混合微粒群算法解决任务调度问题[J].计算机工程与应用,2012,48(12):34-37.
[17]Ertuqrul I,Karakasoqlu N.Performance evaluation of Turkish cement firms withfuzzyanalytic hierarchyprocess and TOPSIS methods[J].Expert Systems with Application,2009,36(1):702-715.
ZENG Wenquan,YU Aimin
School of Computer Engineering&Technology,Guangdong Institute of Science&Technology,Zhuhai,Guangdong 519090,China
To solve the task allocation in virtual enterprise,a multi-object decision-making optimization model on task allocation is constructed.The traditional Particle Swarm Optimization(PSO)algorithm is analyzed.It is improved by automatically adjusting the weight of speed inertia and acceleration coefficient,and by introducing the mutation operation in genetic algorithm.In process of solving the task allocation model by the improved PSO algorithm,the mapping between problems and particles and the computing method of particle position fitness value by Technique for Order Preference by Similarity to Ideal Solution(TOPSIS)are researched.Then,a task allocation algorithm based on the improved PSO algorithm is designed.Finally,the feasibility and validity of the method is verified by an application example and a simulation test.
virtual enterprise;Particle Swarm Optimization(PSO);task allocation;Technique for Order Preference by Similarity to Ideal Solution(TOPSIS)
为了解决虚拟企业中的任务分配问题,建立了任务分配的多目标决策优化模型。分析了传统的PSO算法,通过设置算法中速度惯性权重和加速度系数的自动调整,以及引入遗传算法中的变异操作,实现了对该算法的改进。基于改进的PSO算法求解任务分配模型,研究了求解问题与粒子的映射以及采用TOPSIS计算粒子位置适应度的方法,进而设计了一种基于改进PSO算法的任务分配算法。通过应用实例及仿真实验,证明了改进的PSO算法应用于任务分配的可行性和有效性。
虚拟企业;粒子群优化算法;任务分配;逼近理想解排序
A
TP391
10.3778/j.issn.1002-8331.1211-0032
ZENG Wenquan,YU Aimin.Research on improved PSO algorithm based task allocation.Computer Engineering and Applications,2013,49(13):51-55.
广东省自然科学基金(No.S2011010002537);广东省科技计划项目(No.2012A030400029)。
曾文权(1978—),男,副教授,主要研究方向:计算机应用技术,图像处理和分析;余爱民(1963—),男,博士,教授,主要研究方向:计算机应用技术,图像处理和分析。E-mail:bless365@126.com
2012-11-05
2012-12-31
1002-8331(2013)13-0051-05

