一种新的模糊决策表属性约简方法

徐 山，杜卫锋，闵 啸

1.南京城市职业学院 教务处，南京 210038

2.嘉兴学院 数理与信息工程学院，浙江 嘉兴 314001

一种新的模糊决策表属性约简方法

徐 山1，杜卫锋2，闵 啸2

1.南京城市职业学院 教务处，南京 210038

2.嘉兴学院 数理与信息工程学院，浙江 嘉兴 314001

粗糙集理论研究的核心内容之一是属性重要性的度量和属性约简。应用属性重要性的度量可以分析数据中不同属性的重要程度，从而可以剔除不重要的属性，去掉数据中的冗余成分，保持关键的信息，为科学地管理和决策提供支持。

经典的粗糙集模型适合于处理离散属性值，对于连续属性需要先进行离散化，但是离散化算法往往忽视了不同实值对于离散值的不同的隶属度，导致重要信息的丢失。一种更合理的方法是将模糊集和粗糙集结合，先进行模糊化，将实数值转化为相应的隶属度值，再使用模糊粗糙集进行属性约简[1]。文献[2]提出了一种基于模糊粗糙集的属性约简算法（Fuzzy-Rough Attribute Reduction，FRAR）。实验表明[3]，模糊粗糙属性选择比传统的基于熵、基于主成分分析以及基于随机性的归约技术等方法的效果更好。但是该算法存在有三个问题：（1）该算法的时间复杂度是属性个数的指数阶复杂度[4]，对于有较多属性的模糊决策表，算法并无实用价值。（2）根据该文献上的算例，X={ }x1，x3，x6时，，这与下近似算子是必然性算子的特性相悖。本文采用了另一种不基于模糊划分而是基于元素相关程度的下近似算子，该算子能很好地满足必然性算子的特性。（3）根据实验，在模糊决策表下，要使决策属性对于某条件属性子集的依赖度与决策属性对于条件属性全集的依赖度相等并不容易，此时得到的约简与条件属性全集相差无几，因此，本文提出了相对重要度的概念，通过设置阈值，能得到约简程度较高的近似约简。

1 基本概念

1.1 贴近度

贴近度用于刻画两个模糊集相近的程度，它是一个数量指标。贴近度的定义如下[5]：

定义1设映射N:F(X)×F(X)→[0，1]满足以下条件：

（1）∀A∈F(X)，N(A，A)=1；

（2）∀A，B∈F(X)，N(A，B)=N(B，A)；

（3）若∀A，B，C∈F(X)，∀x∈X满足：

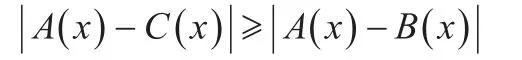
则有N(A，C)≤N(A，B)。则称映射N为F(X)上的贴近度，称N(A，B)为A与B的贴近度。

贴近度有很多具体的表示形式，下面给出其中的一种形式。

定义2设映射N:F(X)×F(X)→[0，1]，∀A，B∈F(X)，当X={x1，x2，…，xn}时，令

可以验证此定义的N(A，B)满足贴近度定义的三个条件。

1.2 依赖度

设(U，R)是模糊信息系统，即R是U上自反的模糊关系。

定义3设(U，R)是模糊信息系统，X⊆U是经典集合，称是X关于(U，R)的模糊下近似，其隶属函数定义为[6]：

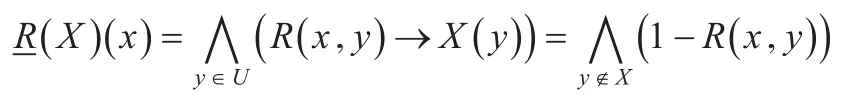
若{x∈U|x∉X}=∅，则说明X=U，此时即

定义4设(U，R)是模糊信息系统，d是U上的经典等价关系，称pοsR(d)是d的R模糊正域，其隶属函数定义为：

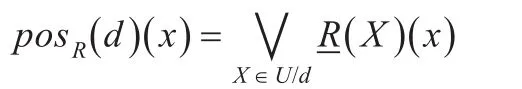
根据模糊正域的定义，d对R的依赖度为：

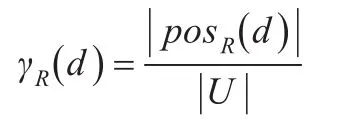
2 借用贴近度定义的模糊关系

如果有若干个模糊集并已知某两个元素对这些模糊集的隶属度，可借用贴近度的定义描述这两个元素之间的关系程度。而贴近度本是用于描述两个模糊集之间的相近程度的。

定义5设R是论域U上模糊关系，已知U上的n个模糊集Ai，i=1，2，…，n。∀x，y∈U，为定义R(x，y)的值，构造另一个论域V={x1，x2，…，xn}，其基数与U上模糊集的数目相等，再构造V上的两个模糊集A和B，∀xi∈V，令A(xi)=Ai(x)，B(xi)=Ai(y)，定义R(x，y)=N(A，B)。

例1有6个模糊集A1，A2，…，A6，已知两个元素x，y对其的隶属度如表1。

构造两个模糊集A和B如表2。

表1 两个元素x，y对模糊集A1，A2，…，A6的隶属度

表2 模糊集A和B

则R(x，y)=N(A，B)。由定义2：

3 一种新的模糊属性约简算法

定义6设有模糊决策表(U,A,d)，B⊆A，令，则称为属性B对于属性A的相对重要度。

模糊决策表属性快速约简算法：

输入模糊决策表(U，A，d)，其中A={a1，a2，…，an}，阈值λ。

输出A的约简Red。

（1）初始化Red=∅；

（2）∀ai∈A-Red，计算，取使值最大的ai，令Red=Red∪{ai}；

4 算例

为了展示该属性约简算法的过程，以文献[2]中给出的一个具体模糊决策表为例展示了该算法的完整操作过程，其中的数据通过编制相应的程序得到。

例2表3给出了一个模糊决策表，该决策表的论域U= {x1，x2，x3，x4，x5，x6}，条件属性集A={a1，a2，a3}和决策属性d，每个条件属性对应论域U上的2个模糊集，而决策属性对应了论域U上的硬划分。设定阈值为λ=0.8。

表3 模糊决策表

根据决策属性d，得到其上的划分：

根据下面将要介绍的方法先行计算得到决策属性d对条件属性全集A的依赖度：

在方法中，关键是要计算在某条件属性集下元素间的关系程度，从而计算在各个属性集下的下近似。仿照例1给出的过程，编程得到在条件属性a1下各元素间的关系程度a1(x，y)（在决策表中，属性集能够生成论域上的二元关系，所以将不再区分属性集和它生成的二元关系，由上下文可自行判断）如表4所示。

表4 在条件属性a1下各元素间的关系程度a1(x，y)

对于元素x1，计算如下：

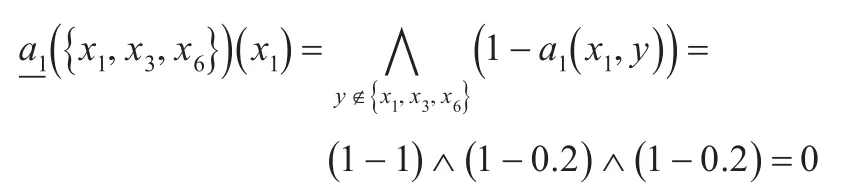
同理可计算得到其他元素的下近似，与元素x1一起列举如下：

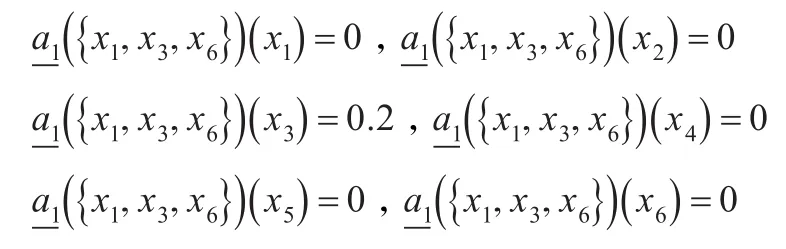
对于第二个决策等价类X={ }x2，x4，x5，也可类似计算得到：

因此每个对象的模糊正域可由定义4求得：

由此可以计算得到决策属性d对条件属性a1的依赖度为：

同理，对于条件属性a2和a3有：

由此发现决策属性d对于条件属性a3的依赖度最大，因此选择属性a3并将之加入约简中。迭代该过程，计算决策属性d对于条件属性集{a1，a3}和{a2，a3}的依赖度如下：

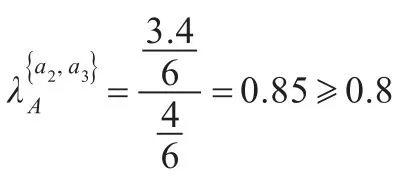
假设模糊决策表有|U|个元素，|A|个条件属性，由上面的计算过程可分析得到本算法的时间复杂度是O(|U|2|A|2)。

5 结论

随着对粗糙集理论研究的不断深入，与其他数学分支的联系也更加紧密。粗糙集理论研究不但需要以这些理论为基础，同时也相应地推动这些理论的发展。特别地，粗糙集理论与其他不确定理论的关系更是引起了广泛关注。文献[7-8]讨论了证据理论中信任函数和似然函数与粗糙集理论中上下近似之间的关系。模糊集和粗糙集理论在处理不确定性和不精确性问题方面都推广了经典集合论，两个理论的结合已经成为粗糙集理论的一个重要分支[9-10]，文献[11-13]给出了模糊粗糙集理论约简方面比较具有代表性的一些算法，文献[14-15]也在不同领域做了有意的尝试。

本文针对FRAR算法的三个问题，采用基于元素相关程度的下近似算子，提出了一种新的模糊决策表的属性约简算法，将原算法由指数复杂度下降为多项式复杂度，实验表明，该算法能处理规模较大的决策表。下一步的研究将从两方面着手：（1）本文提出的用于描述两个元素相关程度的算子随属性数目下降过快，将研究一类其他的算子；（2）本算法的多项式复杂度的阶数还是过高，可通过研究相关算子的性质进一步降低算法的复杂度。

[1]Dubois D，Prade H.Putting rough sets and fuzzy sets together[M]//Intelligent Decision Support.Dordrecht：Kluwer Academic Publishers，1992：203-232.

[2]Jensen R，Shen Q.Fuzzy-rough attribute reduction with application to web categorization[J].Fuzzy Sets and Systems，2004，141（3）：469-485.

[3]Jensen R，Shen Q.Fuzzy-rough data reduction with ant colony optimization[J].Fuzzy Sets and Systems，2005，149（1）：5-20.

[4]王丽，冯山.基于模糊粗糙集的两种属性约简算法[J].计算机应用，2006，26（3）：635-637.

[5]张曾科.模糊数学在自动化技术中的应用[M].北京：清华大学出版社，1997.

[6]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社，2003.

[7]Fagin R，Halpern J Y.Uncertainty，belief，and probability[J]. Comput Intell，1991，7：160-173.

[8]Skowron A.The relationship between the rough set theory and evidence theory[J].Bull Pol Acad Sci Math，1989，37：87-90.

[9]翟兴隆，李续武.基于模糊粗糙依赖度的连续值属性约简[J].计算机工程与应用，2010，46（17）：136-138.

[10]王国胤，姚一豫，于洪.粗糙集理论与应用研究综述[J].计算机学报，2009，32（7）：1229-1246.

[11]彭军峰.一种新的基于模糊粗糙集的连续值属性约简算法[J].电脑知识与技术，2009，5（2）：426-427.

[12]Bhatt R B，Gopal M.On fuzzy-rough sets approach to feature selection[J].Pattern Recognition Letters，2005，26（7）：965-975.

[13]孙如英.基于模糊粗糙集的一种属性约简算法[J].科技信息，2007（35）：681-682.

[14]邱卫根.基于模糊粗集的不完备信息表属性约简算法[J].计算机工程与应用，2005，41（35）：15-16.

[15]樊雷，雷英杰.基于直觉模糊粗糙集的属性约简研究[J].计算机工程与科学，2008，30（7）：79-81.

XU Shan1,DU Weifeng2,MIN Xiao2

1.Dean’s Office,Nanjing City Vocational College,Nanjing 210038,China
2.School of Mathematics,Physics and Information Engineering,Jiaxing University,Jiaxing,Zhejiang 314001,China

The attribute importance measure and attribute reduction is one of the core content of rough sets theory.The classical rough set model based on equivalence relation,is suitable for dealing with discrete attribute values.Fuzzy-rough set theory,combining fuzzy set and rough set theory,extending equivalence relation to fuzzy relation,can deal with fuzzy attribute values.By analyzing three problems of FRAR which is a fuzzy decision table attribute reduction algorithm having extensive use,this paper proposes a new reduction algorithm which has better overcome the problem,can handle larger fuzzy decision table.

rough sets;fuzzy-rough set;fuzzy relation;similarity degree;dependency degree

粗糙集理论研究的核心内容之一是属性重要性的度量和属性约简。经典的粗糙集模型基于等价关系，适合于处理离散属性值。模糊粗糙集理论将模糊集和粗糙集理论结合起来，将等价关系扩展为模糊关系，可处理模糊属性值。分析了已有广泛运用的模糊决策表的属性约简算法FRAR存在的三个问题，提出了一种新的约简算法，较好地克服了原算法的问题，能处理规模较大的模糊决策表。

粗糙集；模糊粗糙集；模糊关系；贴近度；依赖度

A

TP311

10.3778/j.issn.1002-8331.1303-0458

XU Shan,DU Weifeng,MIN Xiao.New method of attribute reduction to fuzzy decision table.Computer Engineering and Applications,2013,49（18）：105-107.

国家自然科学基金（No.61175055，No.61070213）；浙江省自然科学基金（No.LY12A01019，No.LY12F02019）。

徐山（1977—），男，讲师，网络技师，主要研究领域为智能信息处理；杜卫锋（1977—），通讯作者，男，博士，讲师，主要研究领域为粗糙集理论；闵啸（1972—），男，副教授，主要研究领域为最优化理论。

2013-03-28

2013-05-24

1002-8331（2013）18-0105-03