模拟跨导滤波器多目标并行进化的设计

张学华，李 尧

ZHANG Xuehua,LIYao

北华大学 物理学院，吉林 132013

College of Physics,Beihua University,Jilin 132013,China

1 引言

在数据采集、信号处理和实时工程控制等领域，都迫切需要一种能够根据环境变化或人为指导而能自动改变自身参数指标的滤波器，要求这种滤波器能自动跟踪输入信号频率，自动选择合适的滤波器中心频率；应该特别适用于某些宽频率动态范围且有实时性要求的场合。进化硬件（Evolvable Hardware，EHW）既可以满足应用系统的实时性要求，促进系统功能构造智能化发展，又可以提高资源的利用率，降低硬件成本。随着微电子制造和计算机技术的迅速发展，EHW为模拟电子系统设计提供了一条新途径[1-3]，设计思想是：以进化算法特别是遗传算法（Genetic Algorithm，GA）作为组合优化和全局搜索的主要工具[4-5]，将可编程器件作为主要的评估手段和实现载体，试图在不依赖先验知识和外力推动的条件下，通过进化探索更为广阔的设计空间来寻求满足给定要求的滤波器电路结构[6]，进而自动地、实时地重新配置内部电路结构，以适应内部条件（如局部故障）和外部环境（功能要求或物理条件）的变化[7]。这种进化型跨导滤波器不但滤波质量高，而且能够随着外界环境的变化而实时地改变自身的技术参数指标，具有很好的自适应能力和一定的容错能力，是一种很有发展前途的滤波器。本文提出一种模拟跨导滤波器的硬件进化结构和多目标自适应并行进化的设计方法，该方法是利用改进的多目标并行遗传算法（Improved Multiobjective Parallel Genetic Algorithm，IMPGA）实现跨导滤波器的参数优化设计。通过对高Q值的四阶带通跨导滤波器的仿真实验，结果令人满意。

2 模拟跨导滤波器的硬件进化结构

模拟跨导滤波器由跨导放大器、电容和可编程阵列构成，其硬件结构框图如图1所示，可以看出，四个跨导放大器和二个电容元件构成了该模拟跨导滤波器件的一个基本进化单元，其中gm是跨导运算放大器，电容是可编程阻抗阵列。模拟进化硬件由若干个这样的单元串接而成。此进化硬件的结构能被染色体寄存器的二进制位串所改变，且寄存器所存放的可编程位列的当前状态值唯一地决定了硬件的内部连接关系和性能。CPU位于集成电路的外部，是执行遗传算法的进化操作部分，首先通过评价函数对各二进制位串在当前环境下进行全局最优搜索，之后将最优解下载到染色体寄存器，再传送到EHW内部，EHW的结构被这组最优解暂时地唯一确定下来，其性能也随之确定。当运行环境（如温度等）改变，CPU再重新搜索特定条件下的全局最优解，如此反复，EHW的结构总能被特定环境下的全局最优解所决定，从而使EHW达到最优运行状态。

图1 模拟进化型状态变量滤波器硬件结构框图

3 滤波器的进化设计步骤

（1）确定滤波器的实现类型、电路结构及其性能要求。

（2）根据电路结构推导出传递函数，再由传递函数写出各性能指标的数学表达式。

（3）构造适用于进化型跨导滤波器的遗传算法，得到滤波器参数的全局最优解。

（4）将全局最优解匹配到可编程器件中，应用仿真软件验证优化结果。

4 模拟跨导滤波器的进化

4.1 并行遗传算法

并行遗传算法可以提高遗传算法的求解速度和质量[8]。目前，并行遗传算法（Parallel Genetic Algorithm，PGA）主要存在主从式、粗粒度、细粒度和多层的并行化模型[9-10]。粗粒度模型是适应性最强和应用最广的并行化模型[11]。该模型是将随机生成的初始群体依处理器个数分割成若干个子群体。各个子群体在不同的处理器上相互独立地并发执行。每经过一定的进化代，各子群体间会交换若干个体以引入其他子群体的优秀基因，丰富各子群体的多样性，防止未成熟收敛。本文采用粗粒度模型的并行遗传算法并对其进行改进。

PGA的一个重要指标就是迁移率，迁移率的选取是一个很复杂的问题，因为被迁移的往往是子种群中的优秀个体，迁移率大，则有利于优质基因在各个子种群中的传播，但同时增加了通信成本，降低了收敛速度，并且导致种群的多样性迅速下降，找不到满意解。迁移率过小，则又不能有效达到多种群并行计算的目的。

为避免不必要的个体迁移，减少通信代价，提高多群体PGA效率，本文运用基于渗透原理的迁移策略[12]，即设定一个阈值 θ ，0≤θ＜max{|fiti-fitj|}，i，j=0，1，…，n-1，由参考该阈值来确定迁移与否，不再需要人为设定迁移代频、迁移率及迁移方向，算法自身可以自适应地确定何时迁移、迁移多少个体及迁移方向。θ选取应根据算法不同选取不同的值，一般情况下，θ=0有利于优良个体信息的传播。

各子群体初始化后，同时进化。每进化一代比较相邻子群体（它们分别处于状态i，j）的最佳个体适应值。设 fiti，fitj，分别表示子群体状态i，j的最佳个体适应值，计算∆fit=fiti-fitj，迁移率的计算式为：

迁移方向由∆fit的符号确定：∆fit＞0则由i迁移到j；∆fit＜0则由j迁移到i。这样比较相邻子群体的最佳个体，通信量很小。若λ大于零按一定的选择策略选择λN个个体迁移；否则不迁移。接受子群体按一定选择策略，选择λN个个体替换。

4.2 子群体的自适应遗传算法

4.2.1 选择策略

采用赌轮方式进行选择时，如果群体中某一个体的数量多于其他个体，则该个体被选中的机会就远大于其他个体，这样容易导致早熟，使算法提前收敛。改进的期望值法（expected value model）可避免这种情况。

步骤3在[0，1]区间内生成一个均匀分布的伪随机数r，计算F和r的乘积Q，将它作为选择参考概率。

步骤4若Q≤f(V1)，则选择第一个染色体V1，否则选每一个个体的期望值进行取整，按得到的整数安排个体在下一代中的个数。

步骤2计算在步骤1中得到的种群中所有染色体(Vs)择第 k 个染色体Vk(2≤k≤pop_size)，使

步骤5对于期望值的小数部分，可按Bernoulli实验方式进行，将小数方式作为概率进行Bernoulli实验，若实验成功则选择该个体，如此进行下去，直到选满为止。

4.2.2 交叉策略

交叉采用单点交叉与多点交叉两种方式。单点交叉对破坏个体性状、降低个体适应度的可能性最小，因此在迭代后期优良个体较多时，采用单点交叉；多点交叉可能破坏一些好的模式，但同时能够产生较多新的基因块，增加群体多样性，因此在迭代初期优良个体不多时，适合采用多点交叉方式。为提高算法的运行效率和改善算法的收敛性，同时扩大搜索的解空间，以得到更好的最优操作结果。本文对采用两种交叉方式的概率进行规划分配。选择群体适应度的平均值 favg，当个体适应度大于 favg时，较大概率采用单点交叉，当个体适应度小于 favg时，较大概率采用多点交叉。

4.2.3 变异策略

变异本身是一种局部随机搜索与重组算子结合在一起的遗传策略，使GA具有局部搜索能力，保证了GA的有效性；同时“随机”使种群保持了多样性，避免了非全局收敛[13]。在进化初期，需要尽快地在较宽的范围内搜索较优的解，要求变异步长相对较大；当种群锁定到相对较优的范围内时，要求采用较小的变异步长，使搜索更为平滑细致，更有利于找到该局部区域内隐藏的最优解。因此这里采用了步长随世代进化而变化的变异算子：

式中M′为变异后变量取值，M为变异前变量取值，∆L为变量的取值范围，gentime为进化世代数，lchrom为染色体基因座个数，±号由随机数选取。

4.2.4 自适应交叉率和变异率

借鉴生物自适应进化的思想，引入自适应机制，自适应确定Pc和Pm，可较好地解决子群体易早熟收敛和搜索速度缓慢的弊端，克服传统GA的早熟现象，减少进化中后期随机搜索趋势的机率。这里自适应遗传算子采用exp-函数形式，调整如下：

4.2.5 多目标适应度函数的确定

滤波器电路进化设计是典型的多目标优化问题，由于各子目标往往相互冲突，多目标优化通常不存在全局最优解，而仅存在多个甚至无穷多个基于Pareto优于关系的有效解[14-15]。通常希望能够求出全部有效解，或者求出反映其分布规律的有效解子集。常用的“加权和法”通过将各子目标加权求和，将问题简化为单目标优化问题，再利用单目标进化算法求解，即

fi(X)为子目标的向量函数。但这样仅由唯一的权值向量决定的基本搜索方向，故每次运行仅能得到单个最优解，多次运行也无法得到均匀分布的有效解子集[14-15]。本文将次要子目标转化为约束条件，对目标函数作了一定的处理，使其具有相同的数量级，从而达到整体优化的目的。

在对四阶带通跨导滤波器进化过程中，对应每一个染色体可以计算出它的第一级中心频率 f01i，第二级中心频率f02i；增益ki；第一级品质因数为q1i，第二级品质因数为q2i。品质因数 q1i、q2i作为约束条件，满足 9≤q1i≤11，9≤q2i≤11；选择如下适应度函数 F(f01i，f02i，ki)作为每一个染色体的评价标准：F(f01i，f02i，ki)=1/Φ(f01i，f02i，ki)，Φ(f01i，f02i，ki)=ω1|f01i-f0|/a+ω2|f02i-f0|/b+ω3|ki-K|/c，ω1、ω2、ω3为加权值，满足ω1+ω2+ω3=1，a、b、c为常数，取值使适应度函数的目标函数各项在同一数量级上。

5 模拟跨导滤波器进化的仿真实验

以四阶带通跨导滤波器为例来验证模拟进化型跨导滤波器的实效性。设计一个中心频率 f0=1 000 Hz，放大倍数Kv=40，品质因数Q=10的进化型四阶带通跨导滤波器。

四阶带通跨导滤波器可由两级二阶带通跨导滤波器级联构成，每一级的中心频率 f01=f02=1 000 Hz，品质因数Q1=Q2=10。总电压增益 Kv=Kv1·Kv2=40。

对于四阶带通跨导滤波器，染色体长度为10×12{bit}=120 bit。这120 bit唯一确定一种内部结构和功能。在产生初始群体和进化过程中，已实时地剔除了非解染色体，加快了进化的速度。

运用IMPGA实现四阶带通跨导滤波器的参数进化。进化时，随机选取360个个体作为初始群体，分成6个子群体，每个子种群有60个个体，每个子种群独立进化。用长度为10 bit的二进制码串给对应的跨导、电容值编码，编码时要确保跨导和电容的数值基本在同一个数量级上，以减少在计算过程中由于近似计算带来的额外误差。选择策略采用改进的期望值法，交叉策略采用单点交叉和多点交叉相结合的方式，变异策略选取步长随世代进化变化的变异算子，交叉概率和变异概率策略采用exp-函数的自适应概率，适应度函数采用多目标适应度函数，迁移策略选取基于渗透原理迁移策略，阈值θ=0.01，以达到最大世代数得到滤波器最好参数为终止条件。进化后的电路如图2所示，电路元件参数和性能指标如表1所示，跨导单位是mS，电容单位是μF，频率单位是Hz。为了便于比较算法的性能，表1也给出了利用文献[16]中的改进的自适应遗传算法（Improved Adaptive Genetic Algorithm，IAGA）实现四阶带通跨导滤波器参数进化的结果。利用IMPGA进化的结果进行仿真实验，仿真结果如图3所示，图3也给出了两级二阶滤波器的仿真结果。

图2 进化后的四阶带通跨导滤波器

表1 滤波器电路元件参数和性能指标

图3 进化后的四阶带通跨导滤波器的幅频响应

根据表1可以看出利用IMPGA进化的四阶带通跨导滤波器性能指标更准确，与设计的理论值非常接近。由图3可以看出，该滤波器能够满足其在阻带、通带以及过渡带方面的性能要求，衰减特性的通带边缘陡峭，滤波质量高。

表2给出了利用IMPGA和文献[16]中的IAGA分别实现四阶带通跨导滤波器参数进化的算法性能比较。由表2可以看出，把IMPGA应用于该滤波器的进化设计，得到最佳个体的进化代数少，平均运行时间短，进化速度非常快；适应度大，个体性能优良；交叉次数多，个体选择性能好，随机搜索能力强；变异次数也较多，增加群体多样性，避免进化走向局部最优，改善了算法的性能。

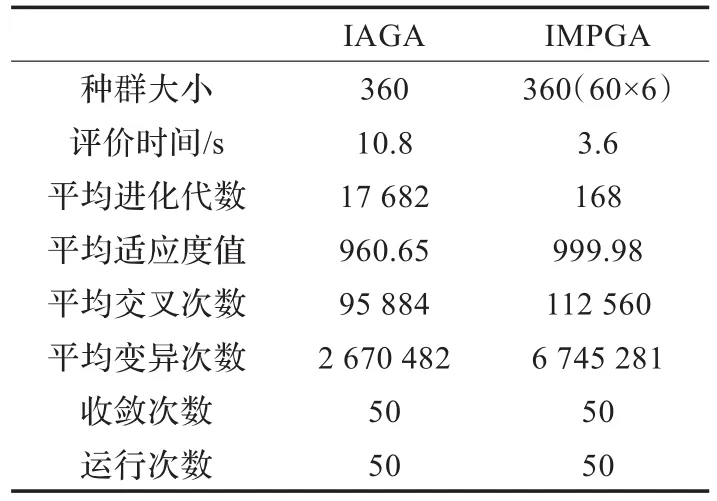
表2 IAGA和IMPGA性能比较

以往通过计算机优化进行滤波器设计的方法大都以目标函数入手，经过梯度算法程序得出问题的解，在数学上要求较高并可能收敛于局部最优解，滤波器的结构和参数往往要人工经过许多次的修改、计算和调试，才能够确定下来，这样耗费人力、物力和财力，设计周期较长；由表2知，把IMPGA应用于四阶带通跨导滤波器的优化设计，经过平均约168代就可以得到最佳个体，平均评价时间3.6 s，进化速度非常快，缩短了设计的周期，从而降低了设计成本。

6 结束语

提出了一种模拟跨导滤波器的硬件并行进化结构，其内部结构能自动地、实时地重新配置，以适应环境的变化。采用级联法所构成的模拟进化型跨导滤波器具有较好的实用性，包括跨导放大器等电路中所有器件都实现了进化，进化的参数值理论结果符合得非常好，能够满足其在阻带、通带以及过渡带方面的性能要求，得到令人满意的结果。由于进化型跨导滤波器可以降低生产中的苛刻条件，参数精度高，参数调节方便，设计快速灵活，设计周期短，设计成本低，电路简单，器件尺寸小，集成度高，抗干扰能力强，功耗低等优点，将成为模拟滤波器的发展方向，对模拟进化型跨导滤波器的研究和设计也就具有更加重要的意义。

[1]Raichman N，Segev R，Ben-Jacob E.Evolvable hardware：genetic search in a physical realm[J].Physica A，2003，326：265-285.

[2]Chen Jongchen，Chen Ruey-Dong.Toward evolvable neuromolecular hardware：a hardware design for a multilevel artificial brain with digital circuits[J].Neurocomputing，2002，42：9-34.

[3]Paola V D，Marijuan P C，Lahoz-Beltra R.Learning and evolution in bacterial taxis：an operational amplifier circuit modeling the computational dynamics of the prokaryotic“two component systems”protein network[J].Bio System，2004，74：29-49.

[4]周明，孙树栋.遗传算法原理及应用[M].北京：国防工业出版社，1999：4-13.

[5]王小平，曹立明.遗传算法——理论，应用与软件实现[M].西安：西安交通大学出版社，2001：74-78.

[6]Thompson A，Layzell P，Zebulum R S.Explorations in design space：unconventional electronics design through artificial evolution[J].IEEE Transactions on Evolutionary Computation，1999，3（3）：167-196.

[7]赵曙光，杨万海，刘喜贵.基于进化的电路自动设计方法[J].电路与系统学报，2002，7（1）：72-78.

[8]李慧贤，程春田.一种基于并行遗传算法的网格资源分配方法[J].计算机工程，2006，32（5）：175-177.

[9]曾国荪，丁春玲.并行遗传算法分析[J].计算机工程，2001（9）：53-55.

[10]张志增，李仲奎，程丽娟.基于主从式并行遗传算法的岩土力学参数反分析方法[J].工程力学，2010，27（10）：21-26.

[11]Lee Y H，Chen C.A modified genetic algorithm for task scheduling in multiprocessor systems[D].Taiwan：National Chiao Tung University，2003.

[12]赖鑫生，张明义.基于渗透原理迁移策略的并行遗传算法[J].计算机学报，2005，28（7）：1146-1152.

[13]余健明，张彦莉.电力网无功优化的一种新算法[J].西安理工大学学报，2005，21（2）：178-182.

[14]Fonseca C M，Fleming P J.An overview of evolutionary algorithms in multi-objective optimization[J].Evolutionary Computation，1995，3（l）：1-16.

[15]Leung Y W，Wang Y P.Multiobjective programming using uniform design and genetic algorithm[J].IEEE Trans on System，Man and Cybernetics-Part C，2000，30（3）：293-304.

[16]李尧，王永超，孙鹏，等.模拟进化型跨导滤波器的研究[J].吉林化工学院学报，2011，28（5）：66-70.