基于离散曲率熵的徘徊行为检测
刘 强 ,罗 斌 ,翟素兰 ,涂铮铮 ,4
LIU Qiang1,2,LUO Bin1,2,ZHAISulan1,3,TU Zhengzheng1,2,4
1.安徽省工业图像处理与分析重点实验室,合肥 230039
2.安徽大学 计算机科学与技术学院,合肥 230039
3.安徽大学 数学科学学院,合肥 230039
4.安徽大学 计算智能与信号处理教育部重点实验室,合肥 230039
1.Key Lab of Industrial Image Processing&Analysis of Anhui Province,Hefei 230039,China
2.School of Computer Science&Technology,Anhui University,Hefei230039,China
3.School of Mathematical Sciences,Anhui University,Hefei 230039,China
4.Key Lab of Intelligent Computing and Signal Processing of Ministry of Education,Anhui University,Hefei 230039,China
1 引言
当今视频监控领域,运动目标的检测和跟踪技术日趋成熟,对跟踪的目标进行分析处理也是当今计算机视觉领域的重要课题,特别是在公共安全的应用前景下,进行视频场景的分析和处理尤为重要。针对公共重点区域的异常行为的检测和分析,长时间进行人工监督和人工分析处理,既不经济又不实用,同时也浪费了大量的存储空间。为了提高监视区域的公共安全性,对区域内行为进行防范,国内外已经有很多学者对异常行为进行研究[1-2],如徘徊行为,徘徊行为常常导致异常情况出现。目前很多学者在基于视频序列的徘徊行为的检测研究上作了很多工作,文献[3]采用了二维马尔可夫随机游走模型,得到基于轨迹内容的时空信息跃迁矩阵,提取其平稳分布和边界穿越可能概率作为最终徘徊判断的准则。文献[4]利用贝叶斯表征跟踪器,对行人的外貌特征进行建模,形成一个候选行人数据库,然后根据保存的时间戳,判断行人行为是否属于徘徊行为,该方法需要建立每个行人的外貌库,过程复杂。
本文从行人的轨迹曲线出发,数学化其运动轨迹的杂乱程度,通过设定关联阈值,进而判断其行人是否是异常行为。本文方法只需计算轨迹,无需建立样本序列库,简单、有效、实时。总体框架流程图如图1所示。
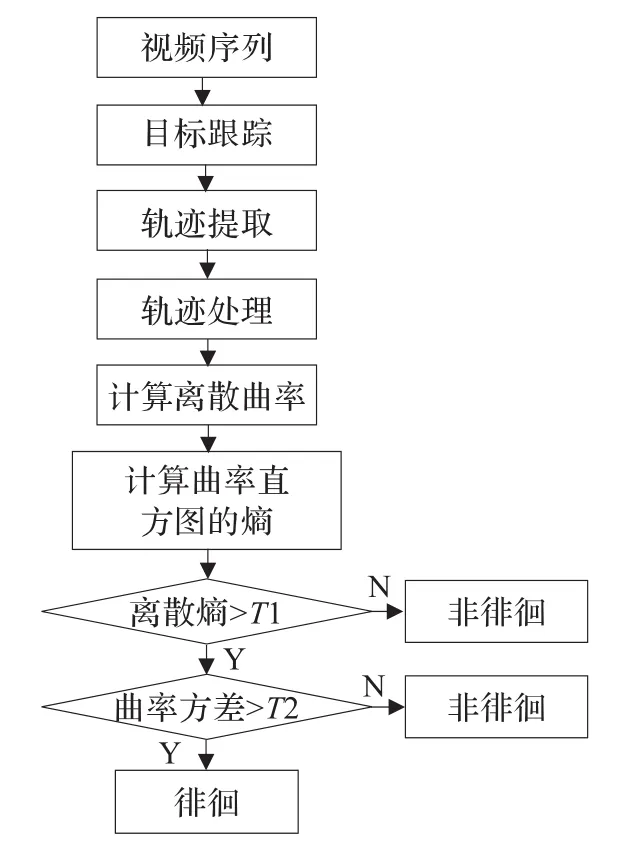
图1 徘徊检测流程图
2 轨迹信息提取与处理
2.1 轨迹提取
目前对于视频序列的运动目标的检测和跟踪算法已经成熟,在视频应用领域已经得到广泛的应用,本文采用Camshift和Kalman预测算法相结合的跟踪算法[5],跟踪效果比较稳定,即使运动目标短暂被遮挡,也具有较好的效果。通过跟踪运动目标得到运动目标质心的运动轨迹,通常这些质心点比较杂乱,会对后续处理带来影响,因此需要通过曲线拟合对这些离散点进行平滑处理。
2.2 轨迹处理
由于得到的整个轨迹离散点杂乱无章,本文采取分段曲线拟合,然后将这些曲线段连接,形成整条运动目标的轨迹曲线。
假设一条轨迹曲线中包含若干个点(x0,y0)、(x1,y1)、…、(xN,yN),从起始点开始到xi值最大处,记为(xm,ym),那么从(x0,y0)到(xm,ym)形成一条曲线段,记为s1,再从(xm+1,ym+1)开始到 xi最小处,记为(xn,yn),那么从(xm+1,ym+1)到(xn,yn)形成一条曲线段,记为s2,如此循环,直到整个轨迹结束,因此就形成了s1~sc若干条曲线段。分别对这些曲线段采取最小二乘法多项式拟合。设拟合公式为:
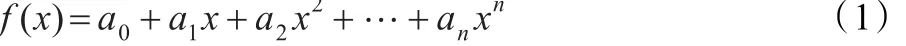
多项式的幂次一般小于7,本文设为6。则节点的偏差的平方和为:
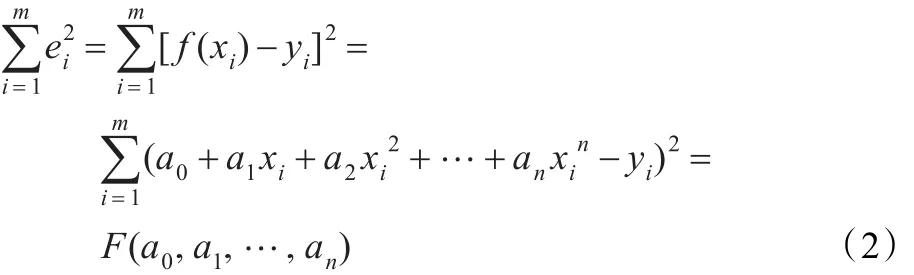
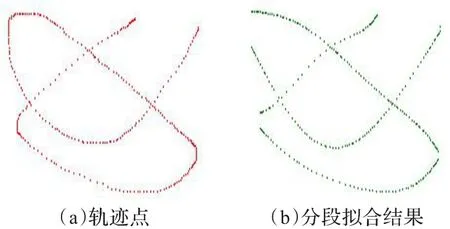
图2 轨迹曲线分段拟合
3 离散曲率的熵和方差
3.1 离散曲率计算
本文中轨迹曲线定义成(Pi)Ni=0=(P0,P1,…,PN),对于离散点 Pi,其离散曲率[6]与相邻点 Pi-1、Pi+1有关,如图3(a)所示,假设该点的离散曲率为 Ki,那么
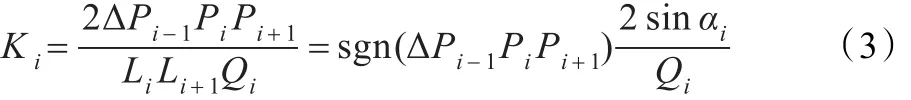
式中,Li=||Pi-Pi-1||,Qi=||Pi+1-Pi-1||,ΔPi-1PiPi+1是有符号的三角形,当 Pi-1,Pi,Pi+1方向是顺时针,Ki定义成正值,表示Pi该点为凸点,反之,当Pi-1,Pi,Pi+1方向是逆时针,Ki定义成负值,表示Pi该点为凹点。对于P0,PN属于特殊考虑点,为起点和终点,曲率计算需特殊考虑,其计算过程如下:
步骤1 假设初始向量 m̂0,终止向量 m̂N,点 P0→ P1→P2来表示 m̂0,点 PN→PN-1→PN-2表示 m̂N,例如,设示,即向量a0、向量b0的数学向量叉乘。m̂0计算[7]如下:
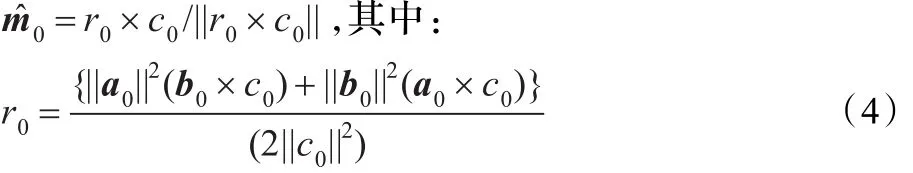
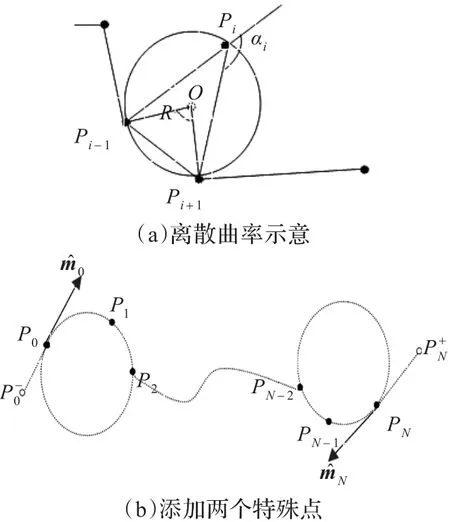
图3 离散点的离散曲率计算
步骤3 P0、PN点的离散曲率采用公式(3)求取。每个点离散曲率的一阶差分也能够被计算出:
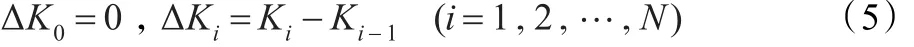
3.2 离散曲率熵以及方差计算
几何学中,曲率能够完全刻画曲线的弯曲程度,而在信息论中熵表示的是数据的杂乱程度,因此本文中徘徊行为的轨迹的杂乱程度用离散曲率的熵表示[8]。熵计算公式如下:
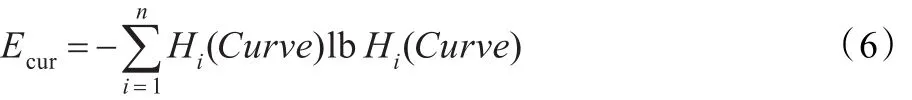
式中Ecur表示离散曲率的熵值,Hi(Curve)表示离散曲率的直方图。Ecur值越大,监视区域内的运动目标轨迹点的分布越杂乱,表示运动目标徘徊的可能性越大。但如果运动目标行走按照S型走出ROI(感兴趣区域)且曲线波动振幅较小,其熵值可能也是比较大的,所以仅仅依靠熵值的判断是不够的,由于方差能够表示数据的偏离程度,所以由方差对徘徊行为作出再判断。方差的公式如下:
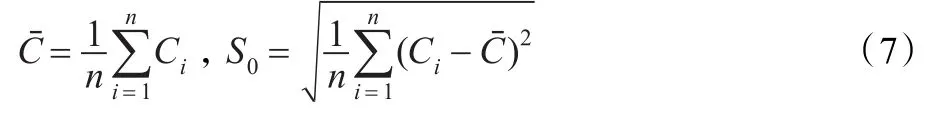
其中Ci表示轨迹中第i个轨迹点的离散曲率值,Cˉ表示轨迹的所有点离散曲率平均值。离散曲率的方差越大,表示偏离程度越大,徘徊的可能性越大,反之亦然。
4 实验结果分析
通过本文方法对几种轨迹样本进行实验,跟踪轨迹图如图4所示,得到轨迹特征值如表1所示,本文判定运动目标是否是徘徊行为,需要选定阈值,通过实验,本文选取熵值阈值 EΔ=1.0,方差阈值 SΔ=0.1。由徘徊行为(1)和(2)可知,曲率熵值Ex大于EΔ时,表示该轨迹杂乱程度较大,但是还需要进一步判断曲率的方差,方差Sx大于SΔ,将其判定为徘徊行为并报警,否则其行为不是徘徊行为。由非徘徊行为(1)可知熵值 Ex小于EΔ时,表示该轨迹杂乱程度较小,将其判定为非徘徊行为。由非徘徊行为(2)可知熵值 Ex大于 EΔ,方差 Sx小于SΔ,将其判定为非徘徊行为。本文采集了10个不同的行人行走视频片段,每组3~8个视频,其中每组中都有若干徘徊与非徘徊行为,通过本文方法对这些样本进行徘徊检测,统计得到正确检测率,结果如表2所示,该方法具有较好的稳定性。另外,Camshift和Kalman相结合的跟踪算法时间耗时约为5 ms,本文的方法平均耗时约为110 ms,因此满足实时性,能够应用到实时视频监控中,目前在徘徊异常检测方面的文献比较少,因此本文仅和文献[3]作了时间比较,比较结果如表1所示,可以看出本文算法在时间性能上的优势。
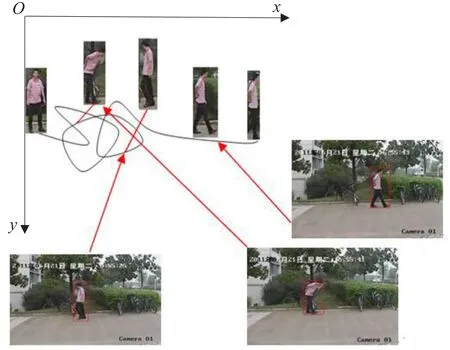
图4 跟踪轨迹示意图

表1 轨迹样本徘徊判定实验结果
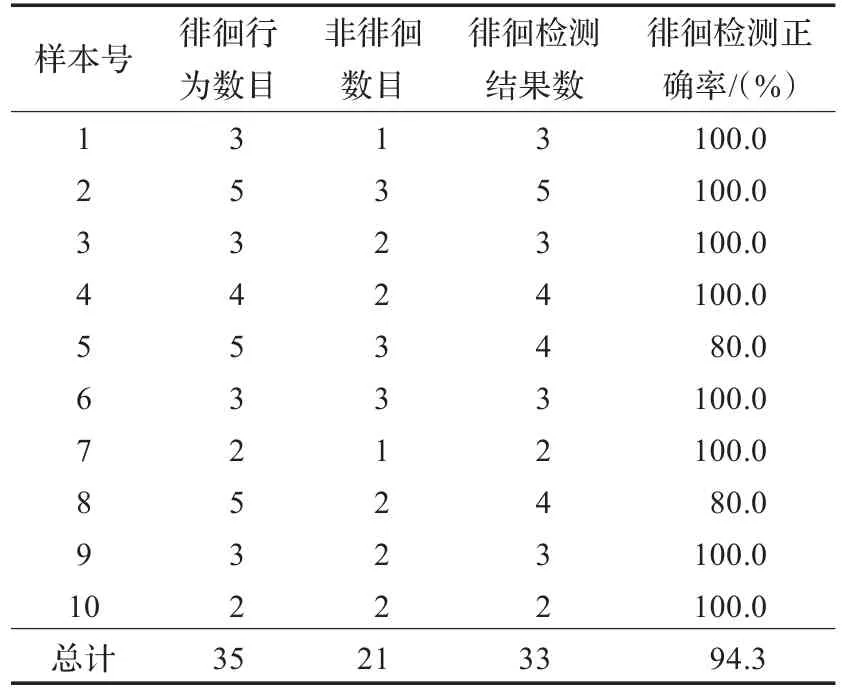
表2 样本检测统计结果
轨迹样本及处理结果如图5所示。

图5 轨迹样本及处理结果
5 结束语
本文通过Camshift和Kalman预测相结合的跟踪算法,对视频序列中的运动目标进行跟踪,将得到的轨迹通过分段曲线拟合进行平滑,计算其曲率熵值和方差,并与熵阈值和方差阈值进行比较,根据判定条件判定是否为徘徊行为。本文方法只需计算运动目标的运动轨迹,无需建立样本库,方法简单、有效、实时。但是本文中的离散熵阈值和方差阈值需要通过统计样本得到经验值,因此,将阈值自适应有待改进。
[1]李和平,胡占义,吴毅红,等.基于半监督学习的行为建模与异常检测[J].软件学报,2007,18(3):527-537.
[2]黄天羽,石崇德,李凤霞,等.一种基于判别随机场模型的联机行为识别方法[J].计算机学报,2009,32(2):275-281.
[3]Zin T T,Tin P,Toriu T.A Markov random walk model for loitering people detection[C]//2010 Sixth International Conference on Intelligent Information Hiding and Multimedia Signal Processing,2010:680-683.
[4]Huang Chung-Hsien,Wu Yita,Shih Ming-Yu.Unsupervised pedestrian re-identification for loitering detection[C]//Lecture Notes in Computer Science:Advances in Image and Video Technology,2009,5414:771-783.
[5]左军毅,梁彦,潘泉,等.基于多个颜色分布模型的Camshift跟踪算法[J].自动化学报,2008,34(7):736-742.
[6]Liu G H,Wong Y S,Zhang Y F.Adaptive fairing of digitized point data with discrete curvature[J].Computer-Aided Design,2002,34:309-320.
[7]Choi B K.Surface modeling for CAD/CAM[M].New York:Elsevier Science Publishers,1991.
[8]Cao Zhisheng,Ma Lin,Wang Naichao.An entropy-based evaluation method of maintenance support system[C]//9th International Conference on Reliability,Maintainability and Safety(ICRMS),2011:842-848.
[9]Piciarelli C,Micheloni C,Foresti G L.Trajectory-based anomalous event detection[J].IEEE Transactions on Circuits and Systems for Video Technology,2008,18:1544-1554.
[10]Bird N,Masoud O,Pananikolopoulos N,et al.Detection of loitering individuals in public transportation areas[J].IEEE Transactions on Intelligent Transportation Systems,2005,6:167-177.
[11]Adam,Rivlin,Shimshoni,et al.Robust real-time unusual event detection using multiple fixed-location monitors[J].IEEE Trans on Pattern Analysis and Machine Intelligence,2008,30(3):555-560.

