直觉模糊层次分析法处理医院用药风险评价

李卫霞，张 昊，张诚一

LIWeixia1,ZHANG Hao2,ZHANG Chengyi3

1.海南医学院 公共卫生学院，海口 571199

2.海南软件职业技术学院 信息管理系，海南 琼海 571400

3.海南师范大学 数学与统计学院，海口 571158

1.School of Public Health,Hainan Medical University,Haikou 571199,China

2.Department of Information Management,Hainan College of Software Technology,Qionghai,Hainan 571400,China 3.School of Mathematics and Statistics,Hainan Normal University,Haikou 571158,China

1 引言

自1980年以来，层次分析法（AHP）[1]及模糊层次分析法（FAHP）[2]的决策理论方法有了很好的实际应用。作为模糊集的推广，在不确定性信息处理与决策方面，直觉模糊集[3]比单值模糊集更具有科学合理、实用性强的特点，然而，也带来了计算的复杂性，为了克服这一矛盾，张诚一[4]提出了直觉模糊集的模糊逼近理论，在此基础上，给出了将直觉模糊互补判断矩阵转换为模糊逼近矩阵[5]，进而提出了直觉模糊环境下的AHP方法，简称为直觉模糊层次分析法。

在社会生活中，重大药品的安全事件发生很多，对人民带来了巨大的创伤和压力，因此药品安全值得特别关注，近年来对用药风险的研究已经从定性研究阶段，提高到对风险评价的量化分析阶段，但是量化处理重大药品安全事件的理论方法并不成熟，本文将直觉模糊层次分析法应用于对医疗机构的用药风险的评价问题，该方法可以提供定性定量结合的风险评价，给出了各子风险类别的权重，是一种实用性较强的医疗机构用药风险评价方法。

2 预备知识

定义 1[6]设判断矩阵 B=(bij)n×n，若 bij∈[0，1](i，j∈N)，bij+bji=1，bii=0.5，则称矩阵B是模糊互补判断矩阵。

定义2[6]设 B=(bij)n×n为模糊互补判断矩阵，若对∀i，j，k∈N ，均有：bij=bik-bjk+0.5，则称 B 是模糊一致性互补判断矩阵。

定义3[3]设X是论域，X的一个直觉模糊集A可以用一个真隶属度函数（又称支持度函数）tA:X→[0，1]和一个假隶属度函数（又称反对度函数）fA:X→[0，1]来刻画，则A可以表示为 A={(tA(x)，fA(x)，πA(x))|x∈X}，其中 0＜tA(x)+fA(x)≤1，πA(x)=1-tA(x)-fA(x)，称 (tA(x)，fA(x))为 A 上的一个直觉模糊值，X上全体直觉模糊集所成集合为V(X)。

为了解决直觉模糊集带来的计算复杂性，利用投票模型解释了直觉模糊集的逼近问题[4]，讨论了第k次投票的结果对第k+1次投票结果的影响，最终给出了无限次投票的极限结果如下：

定义 4[4]设 X 是论域，A={(tA(x)，fA(x)，πA(x))|x∈X}∈FA(x))|x∈X}，称 FA(x)为直觉模糊值(tA(x)，fA(x))的模糊逼近，FA是直觉模糊集A的模糊逼近。

定义5[5]设 B=(bij)n×n是直觉模糊判断矩阵，bij=(tij，1-fij)(i，j∈ N)，且 tij∈[0，1]，fij∈[0，1]，tij=fji，tji=fij，tii=fii=0.5，tij+fij=1，则称矩阵B是直觉模糊互补判断矩阵。

定义6[5]设直觉模糊互补判断矩阵 B=(bij)n×n，其中bij=(tij，1-fij)，πij=1-tij-fij，模糊矩阵 P=(pij)n×n，且 pij=tij/(1-πij)，称模糊矩阵P为B的模糊逼近的模糊互补判断矩阵。

定义7[5]设直觉模糊互补判断矩阵 B=(bij)n×n，其中bij=(tij，1-fij)，P为B的模糊逼近的模糊互补判断矩阵，若P是一致性模糊互补判断矩阵，则称B是一致的。

文献[7]中给出的一种模糊互补判断矩阵的一致性检验调整及排序方法如下：

算法设计1[7]：当模糊互补判断矩阵 P=(pij)n×n不具有满意一致性，采用如下修正方法。

定理1[7]若P为模糊一致性互补判断矩阵，则 pij=β(wi-wj)+0.5(β≥(n-1)/2且为常数)，若 P 为不一致时，则上式不成立，当 β=(n-1)/2解

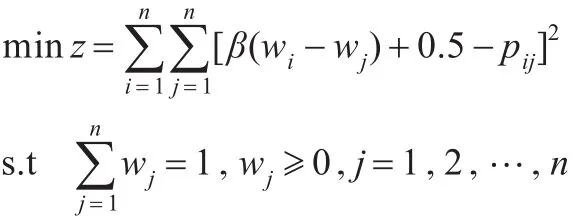
的权重为：

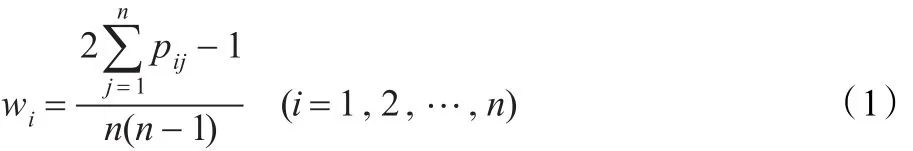
3 基于直觉模糊环境下的AHP

步骤1分析系统中各因素之间的关系，建立系统的递阶结构。

步骤2首先请专家通过对同层属性关于上层属性进行两两比较建立直觉判断矩阵 B=(bij)n×n，其中 bij=(tij，1-fij)，i，j=1，2，…，n ，tij，fij的值根据 0.1～0.9九标度给出的定量标准。然后根据定义6得到模糊逼近的模糊互补判断矩阵P。

步骤3对模糊互补判断矩阵进行一致性检验，利用算法设计1，经过对P进行一致性检验及调整，最后得到满意一致性矩阵。

步骤4计算权重向量。利用式（1）计算各层次构成要素的权重，然后计算最底层构成要素对于总目标的组合权重。

4 基于直觉模糊环境下的AHP在综合医院用药风险评价中的应用

随着社会的发展，医药的种类越来越多、用途和效果也不断增加，然而社会中重大药品的安全事件也日渐频繁，用药的反面作用给人们的用药心理造成了负担，为了减少和解决用药风险问题，近年来对用药风险的研究已经从定性研究阶段，提高到对风险评价的量化分析阶段。

文献[8]利用的模糊层次分析法对各用药风险元素的重要性大小排序，由于在专家给出各个元素的相对重要度时，各专家判断时常常存在不确定度的情况，然而文献[8]没有考虑到这一点，直觉模糊互补判断矩阵体现了决策者对各因素相对重要性的不确定度，于是，将直觉模糊层次分析法应用于对医疗机构的用药风险的评价问题，给出了各子风险类别的权重，是一种实用性较强的医疗机构用药风险评价方法。

下面给出了直觉模糊层次分析法解决医疗机构用药风险元素的评价问题的步骤如下：

步骤1构造评估指标体系，建立递阶结构。根据综合医院用药风险的特点，借鉴文献[8]，综合分析影响综合医院用药风险的各种因素，建立了一套综合医院用药风险评价指标体系。具体结构见表1。

步骤2请多位专家通过对准则层（子准则）各指标关于上层目标层（准则层）的重要性进行两两比较，综合各位专家的意见，建立直觉模糊互补判断矩阵。

表1 综合医院用药风险评价指标体系

其中，第二层准则层中所有元素对目标层的直觉模糊互补判断矩阵为：

依次得到第三层子准则层各元素相对于准则层指标的直觉模糊互补判断矩阵分别为：

上述矩阵的模糊逼近判断矩阵为：

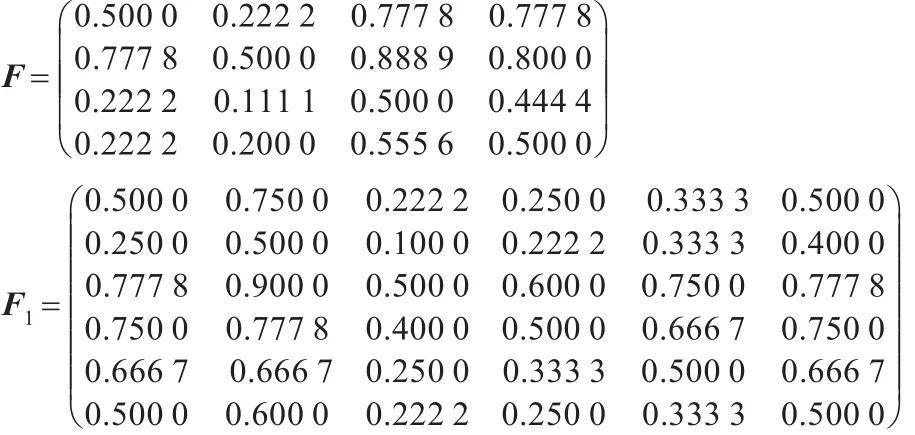
等。

步骤3按算法设计1得到满意一致性矩阵如下：

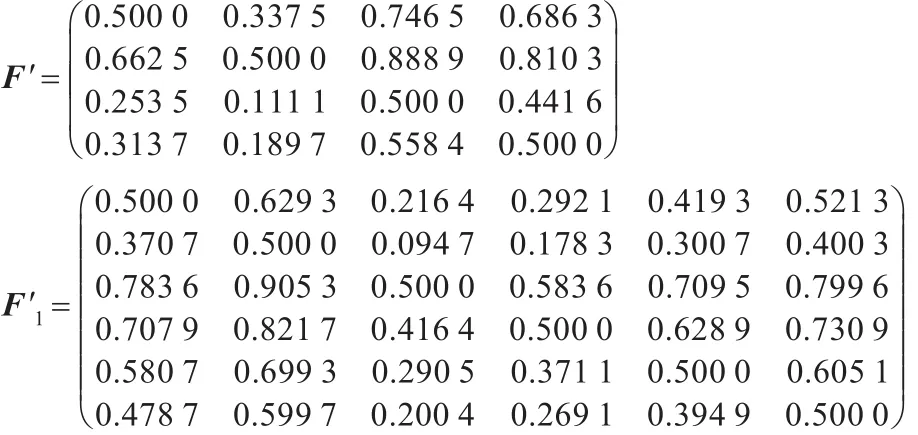
步骤4计算权重向量。根据式（1）计算第二层准则层中所有元素对目标层的权重为：w=(0.2951，0.393 6，0.134 4，0.177)′。同理得到子准则层各元素相对于其上一层各元素的相对权重分别为：

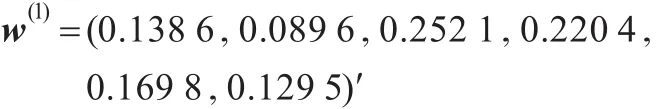
（注：这里 w(i)，i=1，2，3，4，都是23行1列，事实上，所有的子准则元素中对准则层元素不起影响作用的元素权重值为0进行了省略）。因此得到子准则层对于准则层各元素的权重矩阵 W(1)，即 W(1)=(w(1)，w(2)，w(3)，w(4))。集结各层之间的权重。子指标层各元素相对于目标层的元素的组合权重为：

根据以上结果可以看出药物风险在该医院的用药总体风险中比重最大为39.36%，其他风险的重要性依次为机体风险29.51%，技术风险为17.7%，医患风险为13.44%；在药物风险中剂量选择风险所占比例是23个子准则中最大为8.3%，其次比例占第二的是贮存养护风险为7.96%；第三重要的是机体风险中的病理状态风险占7.44%；第四是技术风险中处方审核系统设计风险占6.71%。由上述结论可知，可以对四个风险因素的重要性给出清晰的排序，而且可知得到的准则层四个风险因素的比例相差不是很大。

然而，文献[8]给出的药物风险在该医院的用药总体风险中比重最大为63%，机体风险为23.8%，技术风险为6.6%，医患风险为6.6%。因此其对用药风险因素的重要性比较判断时，得到四因素的重要性相差较大，特别是药物风险的比重占一半以上。

通过比较可知，本文的方法体现了决策者在对因素进行两两比较相对重要度时，考虑了不确定度后将对实际判断有实际意义，实际生活中对于考虑到的风险因素具有重要性应该相差不大，均不可忽视，在进行预防措施时均要重视，这样的结论比其他方法得到的结论更具有实际意义，充分体现了直觉模糊层次分析法的重要作用。

5 结束语

直觉模糊层次分析法把直觉模糊集的优势性质引入了层次分析法，使得人从主观评价时具有考虑犹豫度，是一种更实用的主观判断方法，利用直觉模糊集逼近于模糊集理论来克服运算的复杂性，对实际问题的解决具有说服力。影响医疗机构药品安全的因素众多，患者的安全是非常重要的问题，因此对风险的评价需要有更准确实用的方法，本文利用直觉模糊层次分析法对各风险的重要性做出排序，并且体现了没有忽视相对次要的风险的影响，对医疗机构用药风险的评价有非常重要的意义。

[1]Saaty T L.The analytic hierarchy process[M].New York：Me-Graw-Hill，1980.

[2]张吉军.模糊层次分析法（FAHP）[J].模糊系统与数学，2000，14（2）：80-88.

[3]Atanassov K.Intuitionistic fuzzy sets[J].Fuzzy Sets and Systems，1986，20（1）：87-96.

[4]张诚一，周厚勇.Vague集的模糊逼近与模糊熵相似度量[J].计算机工程与应用，2006，42（33）：20-21.

[5]Zhang Chengyi，Li Weixia，Wang Leng.AHP under the intuitionistic fuzzy environment[C]//2011 8th International Conference on Fuzzy Systems and Knowledge Discovery，2011：583-587.

[6]Orlovsky S A.Decision making with a fuzzy preference relation[J].Fuzzy Sets and Systems，1978，1（3）：155-167.

[7]吴小欢，吕跃进，杨芳.模糊互不判断矩阵的一致性检验及修正[J].模糊系统与数学，2010，24（2）：105-111.

[8]李春慧，施鹏.基于模糊层次分析法的综合医院用药风险评价[J].中国现代医学杂志，2011，21（14）：1685-1687.