粒子群和遗传算法优化支持向量机的破产预测

杨钟瑾

YANG Zhongjin

广东财经大学 信息学院，广州 510320

School of Information Science and Technology,Guangdong University of Finance and Economics,Guangzhou 510320,China

1 引言

破产预测能让人类做出理性的决策，从而最小化风险造成的损失。破产预测广泛应用于各行各业，尤其在学术界和商界备受关注。但是，现实世界所面对的破产预测问题经常是复杂多变和难于捉摸。由于统计模型方法固有的缺陷，因此难于胜任破产预测。与传统的统计模型方法相比，虽然神经网络[1]对破产预测的效果有所改进，但是神经网络具有以下的缺点：（1）难以构建合适的预测模型；（2）常常陷入局部极小值；（3）经验风险最小化原则的运用不能确保良好的推广能力；（4）不容易正确选定训练集的大小。

支持向量机[2]是一种新型的破产预测智能技术，不仅备受瞩目，而且日益盛行。支持向量机以统计学习理论为基础，与神经网络明显不同之处在于运用结构风险最小化原理，克服了神经网络容易陷入局部极小值的问题，提高了推广能力。同时，在运用支持向量机构建预测模型时，在正确选定了核函数[3]的基础上，只需选择最优参数。因此，相对神经网络而言，支持向量机更简易快捷。目前，启发式优化技术[4-5]得到众多研究者的追捧，其中粒子群优化[6]和遗传算法[7]等最为流行，它们都具有并行处理的特征。与其他的优化技术相比，粒子群优化有许多优点：减少内存、快速运算、容易与其他优化技术集成和易于实现。同样，遗传算法也具有以下优点：有效地扫描和探测复杂空间、避免陷入局部极小值、出色地平衡效果与效率之间的关系和不乏灵活性。

Shin等人运用支持向量机预测公司破产，所得预测准确率超过神经网络与其他统计预测方法[8]。Min和Lee采用栅格搜索技术寻找支持向量机最优的核函数参数值，并在此基础上构建破产预测模型，实验结果显示支持向量机的预测准确率高于神经网络与其他统计预测方法[9]。Min等人集成遗传算法与支持向量机来预测破产，采用遗传算法优化特征子集和支持向量机的参数，预测结果表明这种方法优于其他没有优化方法[10]。杨和蒙采用支持向量机在商业银行构建破产预测模型，并将结果与BP神经网络相比，研究结果表明支持向量机优于BP神经网络[11]。Wu等人采用真值遗传算法优化支持向量机的参数，同时构建优化的破产预测模型，实验结果显示这种模型的预测准确率强于神经网络和常规支持向量机[12]。鲁和徐建立基于支持向量机的企业破产分析预测系统模型，实证表明该模型具有良好的预测能力和较强的实用性[13]。Gao等人揉合K-最近邻与支持向量机对公司破产进行预测，这种预测方法比传统支持向量机有更好的分类性能[14]。Zhong等人运用支持向量机构建破产预测模型，实验结果显示该种模型性能优于传统统计模型[15]。Yoon和Kwon运用栅格搜索方法寻找支持向量机的最优参数，并建立模型预测小企业的破产，这种引荐模型的预测性能优于其他模型[16]。Chaudhuri和De运用模糊支持向量机预测上市大公司的破产，与其他方法相比，这种方法改进了预测准确率[17]。Moradi等人运用支持向量机预测上市公司的破产，结果显示该方法的平均预测准确率高于辨别分析方法[18]。

预测准确率取决于支持向量机的推广能力，支持向量机的推广能力又深受相关参数选择所左右。在很多情况下，为某一个问题而选择最优参数是艺术多于科学，而且这其中经常涉及大量的尝试和失败。因此，预测模型的优化经常导致昂贵的过程。本研究将运用粒子群算法和遗传算法优化支持向量机的参数，构建优化的支持向量机预测模型，采用来自UCI机器学习数据库[19]的样本数据并进行归一化数据预处理，将这些引荐方法与随意选择相关参数方法进行比较研究，同时与输入未经预处理的样本原值数据方法比较，由此提出有效优化支持向量机的方法，进而加快支持向量机的学习速度和提高支持向量机的推广性能，从此提高破产预测准确率。

2 支持向量机

支持向量机和核函数方法日愈流行，二者珠联璧合成为核函数支持向量机[20]，同时成功地在预测领域应用。在模式分类与回归分析方面，支持向量机基于统计学习理论和运用VC维思想。支持向量机的基本思想是构造一个超平面作为决策面，由此最大化两类样本的间隔。核函数具有平滑和相似性度量的作用，支持向量机主要由核函数确定。在特征空间中，选择不同形式的核函数就会构成不同的支持向量机，因而也构造出不同的超平面。

在预测领域，径向基核函数是一种常用的核函数，该核函数的表达式如下：

其中，γ是核参数。

在支持向量机的学习过程中，破产公司和非破产公司的样本数据连续地被输入，这些输入数据通过非线性核函数映射到特征空间。在高维特征空间中寻找破产公司和非破产公司样本之间的最大间隔，由此构造超平面的一个最优分界来增强分类性能。因此，可以运用支持向量机预测破产。

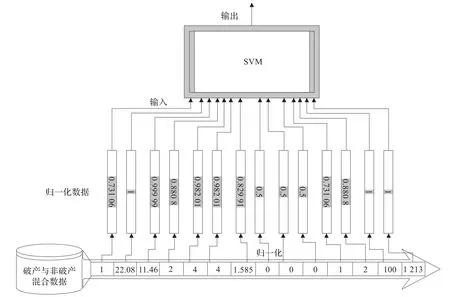
图1 运用支持向量机和归一化输入数据预测破产模型

运用支持向量机预测破产模型如图1，预测模型从混合样本数据集中读取数据，接着归一化预处理这些数据，随后已预处理数据被送进输入空间并转换为输入向量。输入向量经由核函数映射到高维特征空间，在高维特征空间中，通过优化获得一个超平面来分离破产公司和非破产公司的样本，从而实现破产预测功能。

3 粒子群算法和遗传算法

3.1 粒子群算法

粒子群算法是一种新颖且有效的优化智能技术，算法思想来自由个体组成的群体与周边环境以及个体之间互动行为的启示。

在求解优化问题时，个体不仅在搜索空间里有确定的位置，而且具有一定的运动速度，这些个体被称为粒子。根据粒子本身具有最佳性能时所处位置与邻近全局最优粒子的位置，粒子动态地调整它的状态。这个迭代过程直到寻获最优解或是超出了计算限值才终止。在搜索空间里，每个粒子都是一个潜在解，而粒子适应度是评价这些解优劣的标准。粒子适应度计算公式如下：

在此，f(t)为第t回合迭代时当前粒子的适应度，y(t)表示第t回合迭代时当前粒子的实际输出，d(t)代表第t回合迭代时当前粒子的期望输出。

3.2 遗传算法

遗传算法是一种具有随机全局搜索性能的优化智能技术，它模拟自然生物进化原理——适者生存，优胜劣汰。遗传算法根据这个进化原理，将优化问题的求解表示为个体在种群里优胜劣汰的过程，通过对个体进行选择、交叉和变异等遗传操作，实现种群中个体一代接一代地进化，最终获得问题的最优解或满意解。

选择操作确定了新个体基因的来源，在每一代中，选择操作根据种群里个体适应度的评价水平选出优良个体。交叉操作是新个体产生的主要途径，并且决定遗传算法的全局搜索性能，交叉操作是将来自父母代的不同个体基因进行交换和重组，由此产生下一代的新个体。变异操作增加了种群变化的途径，决定局部搜索性能并促进遗传算法收敛于全局最优。变异操作是依据存在于染色体中某个体基因的变异概率而改变这个基因的值，由此产生新的个体。

4 粒子群算法和遗传算法优化支持向量机

正则化参数C和核参数γ是支持向量机的重要参数，这两个参数对支持向量机的预测性能具有深远的影响。在本研究中，将分别运用粒子群算法和遗传算法优化正则化参数C和核参数γ，然后运用优化参数的支持向量机预测破产。

4.1 支持向量机参数

参数选择对支持向量机的推广能力至关重要，因此错误选定参数将极大减弱支持向量机的推广能力。优化支持向量机模型是指为增强推广能力而选定最优参数的过程，决定支持向量机模型性能的参数主要是正则化参数C和核参数γ。正则化参数C协调最小学习误差与最小模型复杂度之间的关系，如果参数C赋值过小，那么就会因为模型过于简单而引起实践风险过高；如果参数C赋值过大，那么就会因为模型过于复杂而过度学习。核参数γ隐式定义了从输入空间到高维特征空间的非线性映射，通常也将这个高水平参数称为超参数，如果参数γ取值过小，那么就会对上界域产生过大影响。虽然支持向量机目前发展得很好，但其目前尚缺乏结构化方法来实现参数的最优选择[21]。在实际应用中，这些最优参数的选择缺乏坚实的理论指导，往往经过多次实验和错误后才能选定。在此，分别通过粒子群算法和遗传算法优化这些参数。

4.2 粒子群算法优化支持向量机过程

粒子群算法依据以下公式调整每个粒子的速度和位置：

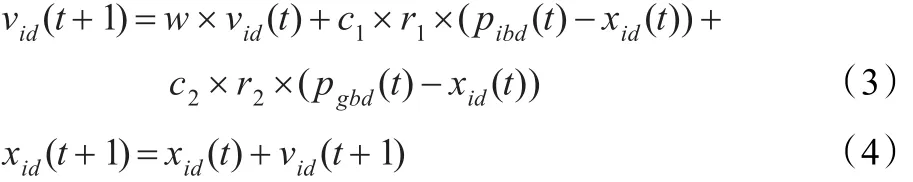
其中，i=1，2，…，m ，d=1，2，…，D ；w 为惯性因子；c1，c2是取值为正的学习因子；r1，r2是取值范围为[0，1]的随机数；vid(t+1)和vid(t)分别代表在第(t+1)回合和第t回合迭代时，第i个粒子在第d维度的速度；xid(t+1)和 xid(t)分别代表在第(t+1)回合和第t回合迭代时，第i个粒子在第d维度的位置；pibd(t)表示第t回合迭代时，第i个粒子在第d维度的最佳位置；pgbd(t)表示第t回合迭代时，整个粒子群在第d维度的最佳位置。

运用粒子群算法优化支持向量机参数过程的概要如图2。

4.3 遗传算法优化支持向量机过程

图3描绘了运用遗传算法优化支持向量机参数过程的概要。

4.4 性能评价

采用预测准确率作为评价支持向量机预测模型性能的指标，同时运用7重交叉校验方法计算和评价模型的预测准确率，这种校验方法确保样本数据集中的每个样本数据都做并且只做一次检验，因此最低程度地减少了因特别选择训练子集和检验子集所带来的结果偏差。在此，PCR表示预测准确率，TQ是指检验样本总数，CQ代表被正确预测的检验样本个数。预测准确率的计算公式如下：

5 结果和讨论

利用Matlab编写程序和进行仿真，相关方法在运行Windows XP的个人计算机（AMD Athlon 64 3200+2 GHz processor；4 GB RAM）上实施与测试。

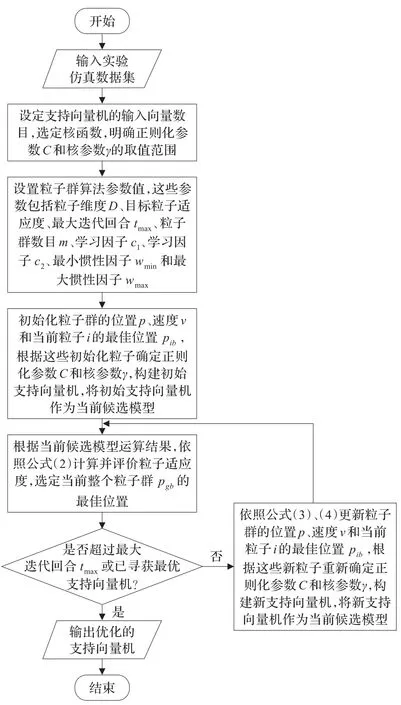
图2 粒子群优化支持向量机参数算法流程图

实验仿真数据源自UCI机器学习数据库的澳大利亚信用数据集，实验仿真数据集由383个破产样本数据与307个非破产样本数据所构成，这个混合数据集共包含690个样本数据。在支持向量机的7重交叉校验仿真实验中，分别从混合数据集中选取370个破产样本数据和295个非破产样本数据作为测试样本数据，这665个样本数据首先随机地分成各自含有95个样本数据的7个子集。每一重交叉校验仿真实验都选取7个子集中的一个子集作为检验集，剩下的6个子集共同构成训练集。最后所得预测准确率是7重交叉校验预测准确率的平均值。

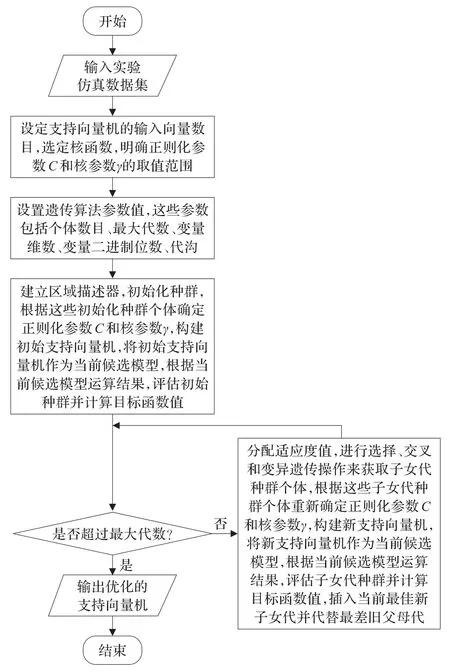
图3 遗传算法优化支持向量机参数算法流程图

在此，粒子群算法和遗传算法的相关参数值是根据预测对象与所获得实验结果而选择设置。在运用粒子群算法优化支持向量机参数过程中，粒子维度设置为2，目标粒子适应度设置为0.001，最大迭代回合设置为3，粒子群数目设置为15，学习因子c1与学习因子c2都设置为1.48，最小惯性因子与最大惯性因子分别设置为0.4和0.9。在运用遗传算法优化支持向量机参数过程中，通过Genetic Algorithm（GA）Toolbox[22]应用软件解决优化问题。采用二进制字符串编码形式，遗传算法的主要参数分别设置为：个体数目等于20，最大代数等于10，变量维数等于2，变量二进制位数等于20，代沟等于0.9。采用随机全体采样选择操作方法，同时采用单点交叉操作方法，并将交叉概率设置为0.7。

在破产预测过程中，预测模型运用二进制支持向量机并通过STPRtool[23]应用软件实现，这些支持向量机由SVMlight[24]软件包（5.00版本）[25]所构建，SVMlight软件包是处理复杂问题的强大优化工具[26]。预测模型的支持向量机采用径向基核函数。表1给出了每一个预测模型的模型名称（MN）、输入数据类型（IDT）、输入向量个数（IVN）、正则化参数（C）、核参数（γ）和输出向量个数（OVN），同时该表也分别列出了各个预测模型的预测准确率（PCR）与平均每一回合模型优化时间（TIME）。

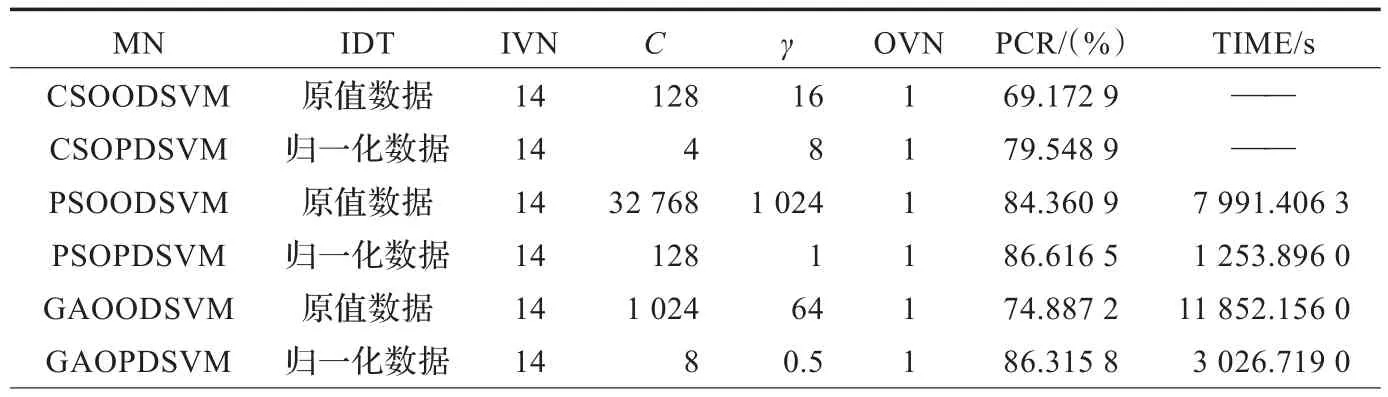
表1 性能比较

从表1可以得到以下观点：

（1）采用经归一化预处理数据时，运用粒子群算法优化支持向量机参数所获得的预测模型PSOPDSVM的预测准确率是86.616 5%，平均每一回合模型优化时间为1 253.896 s；运用遗传算法优化支持向量机参数所获得的预测模型GAOPDSVM的预测准确率是86.315 8%，平均每一回合模型优化时间为3 026.719 s；而随意设置支持向量机参数所获得的预测模型CSOPDSVM的预测准确率仅是79.548 9%。

（2）采用原值数据时，运用粒子群算法优化支持向量机参数所获得的预测模型PSOODSVM的预测准确率是84.360 9%，平均每一回合模型优化时间为7 991.406 3 s；运用遗传算法优化支持向量机参数所获得的预测模型GAOODSVM的预测准确率是74.887 2%，平均每一回合模型优化时间为11 852.156 s；而随意设置支持向量机参数所获得的预测模型CSOODSVM的预测准确率只是69.172 9%。

（3）当采用经归一化预处理数据时，模型PSOPDSVM的预测准确率比模型GAOPDSVM和模型CSOPDSVM的预测准确率分别高出0.300 7%和7.067 6%，模型GAOPDSVM比模型CSOPDSVM的预测准确率高出6.766 9%。模型PSOPDSVM的平均每一回合模型优化时间比模型GAOPDSVM的平均每一回合模型优化时间约少1.4倍。

（4）当采用原值数据时，模型PSOODSVM的预测准确率比模型GAOODSVM和模型CSOODSVM的预测准确率分别高出9.473 7%和15.188%，模型GAOODSVM比模型CSOODSVM的预测准确率高出5.714 3%。模型PSOODSVM的平均每一回合模型优化时间比模型GAOODSVM的平均每一回合模型优化时间约少0.5倍。

（5）预测模型PSOPDSVM的预测准确率比预测模型PSOODSVM的预测准确率高2.255 6%，预测模型GAOPDSVM的预测准确率比预测模型GAOODSVM的预测准确率高11.428 6%，预测模型CSOPDSVM的预测准确率比预测模型CSOODSVM的预测准确率高10.376%。模型PSOODSVM的平均每一回合模型优化时间比模型PSOPDSVM的平均每一回合模型优化时间约多5.4倍，模型GAOODSVM的平均每一回合模型优化时间比模型GAOPDSVM的平均每一回合模型优化时间约多2.9倍。

（6）在预测准确率方面，运用粒子群算法优化支持向量机参数所获得的预测模型比运用遗传算法优化支持向量机参数与随意设置支持向量机参数所获得的预测模型高，运用遗传算法优化支持向量机参数所获得的预测模型比随意设置支持向量机参数所获得的预测模型高，采用经归一化预处理数据比采用原值数据高。

（7）在模型优化时间方面，运用粒子群算法优化支持向量机参数比运用遗传算法优化支持向量机参数少，采用经归一化预处理数据比采用原值数据少。

6 结论和未来研究

本文介绍了运用粒子群算法和遗传算法优化支持向量机参数的研究。此外，针对破产预测构建了二进制支持向量机，采用源自UCI机器学习数据库的破产和非破产混合样本数据集，分别输入未经预处理的原值数据和经归一化预处理的数据进行仿真实验，运用7重交叉校验方法计算和客观地评价模型的预测准确率。仿真实验证明，运用粒子群算法和遗传算法优化支持向量机参数有效地加速学习和提高推广性能，从而进一步提高破产预测准确率。同时，采用经归一化预处理数据可以进一步提高破产预测准确率。实验结果比较分析表明，在支持向量机预测模型优化方面，无论是预测准确率或模型优化时间，粒子群算法都强于遗传算法。

支持向量机由于不同核函数的构造和选择而各异，核函数的合理构造与正确选择是支持向量机执行学习过程的重要一步，并且对支持向量机性能有至深的影响。为特定问题而构造和选择核函数是一个耗时与耗力的过程，因此，如何构造与如何选择最优核函数是亟需有待进一步研究的重要问题。

[1]Haykin S.Neural networks：a comprehensive foundation[M].Upper Saddle River，NJ，USA：Prentice Hall，1998.

[2]Vapnik V.The nature of statistical learning theory[M].New York：Springer-Verlag，1995.

[3]Schoelkopf B，Smola A.Learning with kernels[M].Cambridge，Massachusetts：The MIT Press，2002.

[4]Jiao Licheng，Li Yangyang，Gong Maoguo，et al.Quantum-inspired immune clonal algorithm for global optimization[J].IEEE Transactions on Systems，Man，and Cybernetics，Part B（Cybernetics），2008，38（5）：1234-1253.

[5]Karaboga D，Basturk B.On the performance of artificial bee colony algorithm[J].Applied Soft Computing，2008，8（1）：687-697.

[6]Kennedy J，Eberhart R C.Particle swarm optimization[C]//Proceedings of IEEE International Conference on Neural Networks.Piscataway：IEEE Press，1995：1942-1948.

[7]Goldberg D E.Genetic algorithms in search，optimization and machine learning[M].New York：Addison-Wesley，1989.

[8]Shin K，Lee T S，Kim H.An application of support vector machines in bankruptcy prediction model[J].Expert Systems with Applications，2005，28（1）：127-135.

[9]Min J H，Lee Y.Bankruptcy prediction using support vector machine with optimal choice of kernel function parameters[J].Expert Systems with Applications，2005，28（4）：603-614.

[10]Min S，Lee J，Han I.Hybrid genetic algorithms and support vector machines for bankruptcy prediction[J].Expert Systems with Applications，2006，31（3）：652-660.

[11]杨毓，蒙肖莲.用支持向量机（SVM）构建企业破产预测模型[J].金融研究，2006（10）：65-75.

[12]Wu C，Tzeng G，Goo Y，et al.A real-valued genetic algorithm to optimize the parameters of support vector machine for predicting bankruptcy[J].Expert Systems with Applications，2007，32（2）：397-408.

[13]鲁海波，徐云.基于支持向量机的企业破产分析[J].数学的实践与认识，2007，37（12）：13-18.

[14]Gao Zhong，Cui Meng，Po Laiman.Enterprise bankruptcy prediction using noisy-tolerant Support Vector Machine[C]//2008 International Seminar on Future Information Technology and Management Engineering.Leicestershire：IEEE Press，2008：153-156.

[15]Zhong Ping，Xi Bin，Cen Yong.Support Vector Machines modeling for prediction[J].International Journal of Systems and Control，2008，1：42-47.

[16]Yoon J S，Kwon Y S.A practical approach to bankruptcy prediction for small businesses：substituting the unavailable financial data for credit card sales information[J].Expert Systems with Applications，2010，37（5）：3624-3629.

[17]Chaudhuri A，De K.Fuzzy Support Vector Machine for bankruptcy prediction[J].Applied Soft Computing，2011，11（2）：2472-2486.

[18]Moradi M，Sardasht M S，Ebrahimpou M.An application of Support Vector Machines in bankruptcy prediction evidence from Iran[J].World Applied Sciences Journal，2012，17（6）：710-717.

[19]Asuncion A，Newman D J.UCI machine learning repository[EB/OL].[2012-03-14].http：//archive.ics.uci.edu/ml/datasets.html.

[20]杨钟瑾.核函数支持向量机[J].计算机工程与应用，2008，44（33）：1-6.

[21]顾亚祥，丁世飞.支持向量机研究进展[J].计算机科学，2011，38（2）：14-17.

[22]Andrew C，Peter F，Hartmut P，et al.Genetic Algorithm toolbox user’s guide[R].Sheffield：University of Sheffield，1994.

[23]Franc V，Hlava V.STPRtool[EB/OL].（2004-12-14）.http：//cmp.felk.cvut.cz/cmp/cmp software.html.

[24]Joachims T.Making large-scale SVM learning practical[C]//Advances in Kernel Methods—Support Vector Learning.Cambridge，MA：MIT Press，1999：169-184.

[25]Joachims T.SVMlight software[EB/OL].（2002-03-14）.http：//svmlight.joachims.org/.

[26]Franc V，Hlava V.Statistical pattern recognition toolbox for Matlab user’s guide[EB/OL].（2004-06-24）.ftp：//cmp.felk.cvut.cz/pub/cmp/articles/.