外P-集合副集的τ-生成与τ-强生成

于秀清，董立华，张玉坤

德州学院 数学系，山东 德州 253023

外P-集合副集的τ-生成与τ-强生成

于秀清，董立华，张玉坤

德州学院 数学系，山东 德州 253023

P-集合是由内P-集合与外P-集合XF构成的集合对()。它是将动态特性引入有限非空普通集合X，对其进行改进得到的。设集合X={x1，x2，…，xm}，α= {α1，α2，…，αk}是X的属性集合。若α外的某些属性被迁入α内，α内的属性增加，相应地，集合X内的某些元素就被迁出X，X里面的元素减少，X变成内P-集合另一方面，若α内的部分属性被迁出α，α内的属性减少，相应地，集合X外的某些元素就被迁入X，X里面的元素增加，X变成外P-集合XF。内P-集合与外P-集合XF是集合X的动态特性的具体表现。P-集合是一个研究动态问题的新的数学理论工具，近几年得到广大学者的关注与研究，在多个领域获得了应用。文献[1-4]给出了P-集合特性讨论，文献[5-12]给出了P-集合在信息系统、控制系统中的应用。

深入分析集合X变化到外P-集合XF的动态过程，容易发现：元素迁移f∈F对元素i=1，2，…，t，进行迁移的结果有三种：（1）yi仍在集合X外；（2）yi被完全迁入集合X；（3）yi被部分迁入集合X。外P-集合只考虑了前两种结果，忽略了第三种结果，或者说，外P-集合是在假设第三种结果不会发生的前提下进行的定义。但在控制系统、信息系统中，确实存在元素被部分迁入集合的情况，而且这些被部分迁入的元素对系统本身的影响是不容忽视的，有时甚至是相当大的。例如，国内生产太阳能的企业构成集合X={x1，x2，…，xn}，α={α1，α2，…，αn′}是影响太阳能企业发展的因素构成的集合，或者，α是X的属性集合。由于国内外大力提倡发展与利用清洁新能源，国家放宽了生产太阳能产品的政策，太阳能经济得到快速发展，某些不景气的其他企业转行加入到太阳能企业的行列，还有一部分企业在保留部分原来产品生产的基础上，进行太阳能产品的生产。这样在进行太阳能市场分析时，就需要考虑三方面的情况：原有太阳能企业、新加入的太阳能企业与部分进行生产太阳能产品的企业。当部分进行生产太阳能产品的企业所占太阳能市场的份额很大的时候，必须要考虑其在太阳能产品生产中的影响，否则分析结果就会与实际情况偏差很大，进而作出错误的决策。基于此，本文给出外P-集合的副集、外P-集合副集τ-生成与外P-集合副集τ-强生成的概念与结构，从理论的角度讨论了外P-集合副集、外P-集合副集τ-生成与τ-强生成之间的关系，得到外P-集合副集、外P-集合副集τ-生成与τ-强生成的性质定理，对P-集合理论进行了补充，扩展了P-集合的应用范围。

为了更容易接受本文的研究结果，简要介绍了外P-集合的概念与结构，关于外P-集合与P-集合的更多更详细的讨论与应用见文献[1-12]。

1 P-集合的概念与结构

约定：U是有限元素论域，X⊂U是有限非空元素集合；V是属性论域；，f∈F是元素迁移，={f1，f2，…，ft}是元素迁移族；card=cardinal number（基数），UNI=unidentification（不可辨识），IED=identification（可辨识）。

给定有限非空集合X={x1,x2,…,xq}⊂U,α={α1，α2，…，αk}⊂V是X的属性集合，称XF是X生成的外P-集合，简称XF是外P-集合，而且：

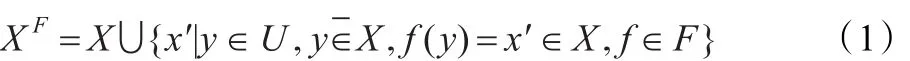
利用式（1）给出的结构，容易得到下面外P-集合XF与普通集合X之间的关系定理。

定理1.1（外P-集合XF与集合X关系定理）外P-集合XF与普通集合X满足：

特别地，当F=F=ϕ时，UNI(X，XF)。

2 外P-集合副集的τ-生成与τ-强生成

定义2.1设X={…，xn}⊂U，给定元素y∈U、、元素迁移f∈F，如果f(y)∈X，称元素y对于集合X是全迁入，f(y)的特征函数χf(y)满足χf(y)=1。

给定元素y∈U、、元素迁移f∈F，如果称元素y对于集合X是零迁入，f(y)的特征函数χf(y)满足χf(y)=0。

给定元素y∈U、、元素迁移f∈F，如果称元素y对于集合X是部分迁入，f(y)的特征函数χf(y)满足0＜χf(y)＜1。这里，表示元素迁移f∈F把部分迁入集合X内。

定义2.2称集合Α(XF)是外P-集合XF的副集（assistant set），简称Α(XF)是外副集，如果

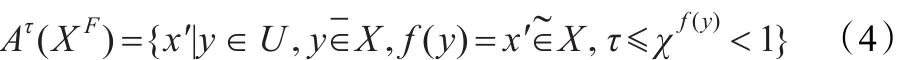
称是外P-集合副集的τ-生成（τ-generation of assistant set of outer P-set），简称外副集Α(XF)的τ-生成，如果称Ατ˙(XF)是外P-集合副集的τ-强生成（τ-strong generation of assistant set of outer P-set），简称外副集Α(XF)的τ-强生成，如果

其中0＜τ＜1。

在定义2.1中，由于元素迁移f∈F的作用，产生了元素补充集合{x′|y∈U，f(y)=x′∈X，f∈F}与外副集Α(XF)={x′|y∈U，=。元素补充集合是由被完全迁入集合X的元素构成的集合，外副集是由被部分迁入集合X的元素构成的集合。外P-集合没有考虑被部分迁入的元素，仅仅考虑了被全部迁入的元素。但在实际问题中被部分迁入的元素也会对问题的研究产生很大的影响。由于不同的实际问题要求的精确度不同，进而提出外副集的τ-生成与τ-强生成的概念，这样可以根据实际情况选择不同的参数τ。

由定义2.1与定义2.2可以直接得到命题2.1～2.5、定理2.1与定理2.2成立。

命题2.1 当F=时，对 ∀τ∈(0，1)都有Ατ˙(XF)=Ατ(XF)=Α(XF)=XF=。

命题2.2对∀τ∈(0，1)，Ατ(XF)=的充分必要条件是Α(XF)=。

命题2.3对∀τ∈(0，1)，Ατ˙(XF)=的充分必要条件是Α(XF)=。

命题2.4对∀τ∈(0，1)，Ατ˙(XF)=的充分必要条件是Ατ(XF)=。

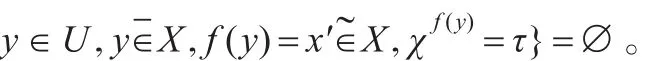
定理2.1（外副集与其τ-生成、τ-强生成关系定理）设Ατ˙(XF)，Ατ(XF)分别是外副集Α(XF)的τ-生成与τ-强生成，则对∀τ∈(0，1)，有

定理2.2（集合X与外副集关系定理）设Α(XF)是外P-集合XF的副集，则

推论2.1设Ατ(XF)是外副集Α(XF)的τ-生成，则对∀τ∈(0，1)，有

推论2.2设Ατ˙(XF)是外副集Α(XF)的τ-强生成，则对∀τ∈(0，1)，有

3 外副集的τ-生成与它的性质定理

定理3.1（外副集Α(XF)的τ-生成、τ-强生成关系定理）Ατ˙(XF)，Ατ(XF)分别是外副集Α(XF)的τ-生成与τ-强生成，对∀τ1，τ2∈(0，1)，若τ1＜τ2，则

这里仅给出（1）的证明，（2）与（3）的证明类似，略。

证明对∀x′∈、元素迁移f∈F，令满足f(y)=x′，由式（9）知，f(y)=x′的特征函数χf(y)满足τ2＜χf(y)＜1，因为τ1＜τ2，所以f(y)=x′的特征函数χf(y)满足τ1≤χf(y)＜1，故x′∈，（1）成立。

推论3.1设分别是外副集Α(XF)的τ-生成与τ-强生成，对∀τ1，τ2，…，τt∈(0，1)，若τ1＜τ2＜…＜τt，则

推论3.2设分别是外副集Α(XF)的τ-生成与τ-强生成，则(Ατ(XF)，⊆)、(Ατ˙(XF)，⊆)是全序集。

推论3.3设Ατ˙(XF)，Ατ(XF)分别是外副集Α(XF)的τ-生成与τ-强生成，I是有限指标集合，∀i∈I，τi∈(0，1)有

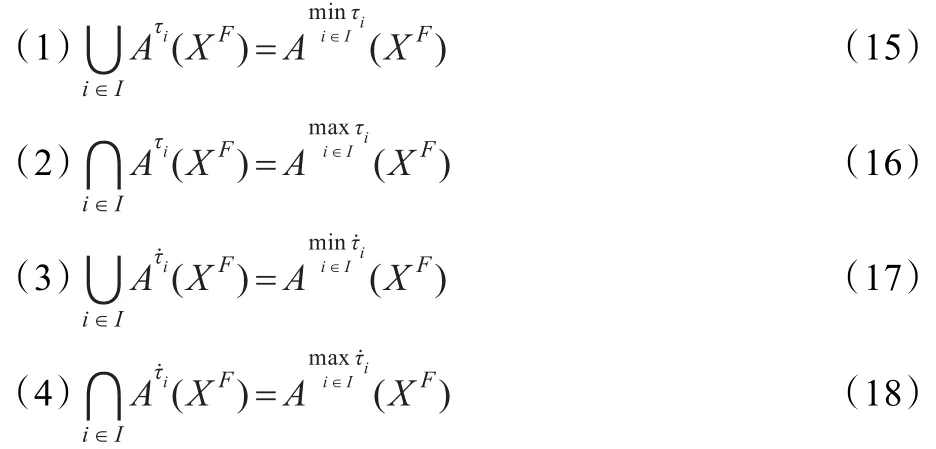
定理3.2（外副集的生成定理）设Ατ˙(XF)，Ατ(XF)分别是外副集Α(XF)的τ-生成与τ-强生成，则

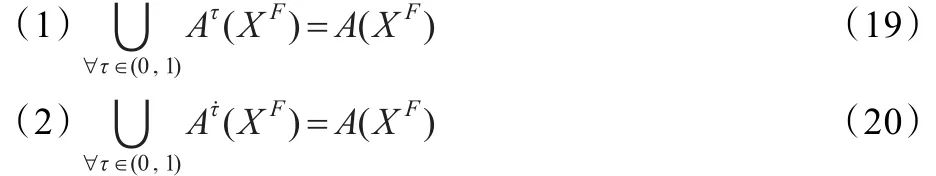
定理3.3（外副集的τ-生成不可辨识定理）设Ατ(XF)是外副集Α(XF)的τ-生成，若存在τ1，τ2∈(0，1)，τ1＜τ2，满足UNI(Ατ1(XF)，Ατ2(XF))，则对∀τ*∈[τ1，τ2]，都有：

定理3.4（外副集的τ-强生成不可辨识定理）设Ατ˙(XF)是外副集Α(XF)的τ-强生成，若存在τ1，τ2∈(0，1)，τ1＜τ2，满足UNI(Ατ˙1(XF)，，则对∀τ*∈[τ1，τ2]，都有：

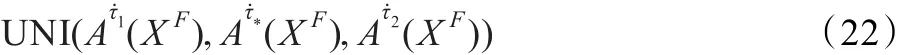
定理3.4的证明与定理3.3类似，略。

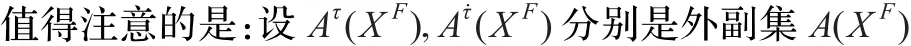
由以上分析得到定理3.5成立。

定理3.5（外副集τ-生成与τ-强生成不可辨识定理）设Ατ(XF)，Ατ˙(XF)分别是外副集Α(XF)的τ-生成与τ-强生成，若存在τ1，τ2∈(0，1)，τ1＜τ2，满足 UNI()，则对∀τ*∈[τ1，τ2)，都有：

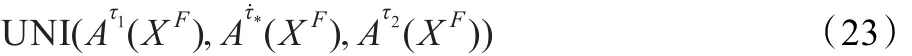
由定理3.2～3.5可以直接得到推论3.4～3.6。

推论3.4设Ατ(XF)，Ατ˙(XF)分别是外副集Α(XF)的τ-生成与τ-强生成，若存在τ1，τ2∈(0，1)，τ1＜τ2，满足UNI(Ατ˙1(XF)，Ατ˙2(XF))，则对∀τ*∈(τ1，τ2)，都有：

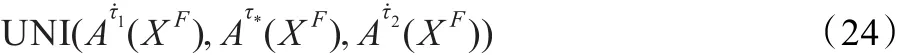
推论3.5设Ατ˙(XF)是外副集Α(XF)的τ-强生成，若UNI(Ατ(XF)，Α(XF))，则对∀τ*∈(0，τ)，都有：

推论3.6设Ατ(XF)分别是外副集Α(XF)的τ-生成，若UNI(Ατ(XF)，Α(XF))，则对∀τ*∈(0，τ]，都有：

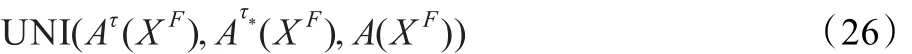
推论3.7设Ατ(XF)是外副集Α(XF)的τ-生成，若存在τ1，τ2∈(0，1)，τ1＜τ2，满足 IDE(Ατ1(XF)，Ατ2(XF))，则对∀τ*∈(0，τ1)，都有：

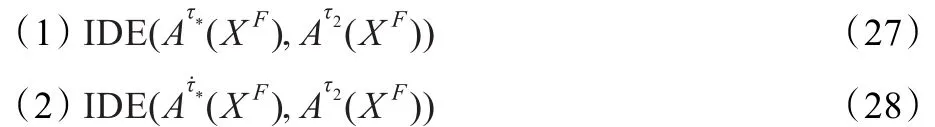
4 讨论

P-集合具有动态特性，是研究动态系统的一个有利的数学理论工具。但由于外P-集合是在假设集合中元素被全部迁入的前提下进行的研究，外P-集合在实践中的应用受到了一定程度的限制。外P-集合的副集与外P-集合副集的τ-生成、τ-强生成的提出弥补了P-集合理论的不足，扩大了P-集合的应用领域。

[1]史开泉.P-集合[J].山东大学学报：理学版，2008，43（11）：75-84.

[2]于秀清.P-集合的动态特性[J].计算机工程与应用，2010，46（18）：45-48.

[3]Huang Shunliang，Wang Wei，Geng Dianyou.P-sets and its internal P-memory characteristics[J].An International Journal Advances in Systems Science and Applications，2010，10（2）：216-222.

[4]Huang Shunliang，Wei Wang，Geng Dianyou.P-Sets and its P-separation theorems[J].An International Journal Advances in System Science and Application，2010，10（2）：245-251.

[5]Lin Rong，Fan Chengxian.Packet sets and identification of inward-convergence information[J].An International Journal of Convergence Information Τechnology，2012，7（7）：157-164.

[6]张飞，陈萍，张丽.P-集合的P-分离与应用[J].山东大学学报：理学版，2010，45（3）：18-22.

[7]史开泉，张丽.外P-集合与数据外-恢复[J].山东大学学报：理学版，2009，44（4）：8-14.

[8]于秀清.P-集合与F-外嵌入信息辨识-发现[J].计算机科学，2010，38（1）：250-253.

[9]Zhang Guanyu，Li Enzhong.Information gene and its information knock-out/knock-in[J].An International Journal Advances in Systems Science and Applications，2010，10（2）：267-275.

[10]Liu Jiqin.P-probabilities and its application[J].An International Journal Advances in Systems Science and Applications，2010，10（2）：237-244.

[11]李豫颖.F-畸变数据的生成与修复[J].吉首大学学报：自然科学版，2010，31（3）：59-72.

[12]于秀清.迭代F-外嵌入信息生成及其遗传发现-应用[J].系统工程与电子技术，2011，33（12）：2691-2695.

YU Xiuqing,DONG Lihua,ZHANG Yukun

Department of Mathematics Science,Dezhou University,Dezhou,Shandong 253023,China

P-sets（Packet sets）is a pair of sets composed of internal P-set（internal Packet set）and outer P-set（outer Packet set）, which has dynamic characteristics.Based on outer P-set,some concepts related to outer P-set are proposed,such as assistant set of outer P-set,τ-generation of assistant set of outer P-set,τ-strong generation of assistant set of outer P-set,and so on.Furthermore,the relationships among them are discussed.And their relation theorems,identified theorems,unidentified theorems and generation theorems of assistant set of outer P-set are obtained.Τhe theory of P-sets is supplemented.

outer P-set;assistant set of outer P-set;τ-generation of assistant set of outer P-set;τ-strong generation of assistant set of outer P-set;identification theorems

P-集合是由内P-集合与外P-集合构成的集合对，它具有动态特性。在外P-集合的基础上，定义了外P-集合的副集Α(XF)、外P-集合副集τ-生成Ατ(XF)与外P-集合副集τ-强生成Ατ˙(XF)，讨论了三者之间的关系，得到外P-集合副集τ-生成与外P-集合副集τ-强生成关系定理、辨识定理与外P-集合副集的生成定理。对P-集合理论进行了补充。

外P-集合；外P-集合的副集；外P-集合副集的τ-生成；外副集的τ-强生成；辨识定理

A

O159

10.3778/j.issn.1002-8331.1208-0030

YU Xiuqing,DONG Lihua,ZHANG Yukun.τ-generation andτ-strong generation of assistant set of outer P-set.Computer Engineering and Applications,2013,49（15）：41-43.

山东省高校科技计划资助项目（No.J12LN92）；山东省自然科学基金（No.ZR2010AL019）；山东省科技发展计划资助项目（No.2011GGA14074）。

于秀清（1968—），女，教授，研究领域为粗系统理论与应用，信息系统理论与应用。E-mail：sddzyxq@163.com

2012-08-02

2012-10-16

1002-8331（2013）15-0041-03