三角代数上中心化子的刻画

马 飞，张建华，李 莉，任刚练

1.陕西师范大学 数学与信息科学学院，西安 710062

2.咸阳师范学院 数学与信息科学学院，陕西 咸阳 712000

3.西安工程大学 理学院，西安 710048

三角代数上中心化子的刻画

马 飞1，2，张建华1，李 莉3，任刚练2

1.陕西师范大学 数学与信息科学学院，西安 710062

2.咸阳师范学院 数学与信息科学学院，陕西 咸阳 712000

3.西安工程大学 理学院，西安 710048

1 引言

设Α是一个环或代数，如果可加映射φ:Α→Α满足对任意的a，b∈Α有φ(ab)=φ(a)b，那么称φ是一个左中心化子；类似的可以定义右中心化子。如果φ既是左中心化子又是右中心化子，那么称φ是中心化子。与中心化子密切相关的一类重要映射是中心化映射，若映射φ:Α→Α满足对任意的a∈Α，有φ(a)a-aφ(a)∈Z(Α)（Z(Α)为Α的中心），则称映射φ是中心化的；特别的，若φ(a)a=aφ(a)，则称映射φ是可交换的。

关于具有满足哪些条件的映射为中心化子的研究一直深受许多学者的关注，但是大多都要求环或代数具有素或半素性，如Brešar在文献[1]中证明了若半素环R上的映射φ既是左Jordan中心化子，又是右Jordan中心化子，则存在λ∈C（R的扩展中心），使得φ(a)=λa对任意的a∈R都成立；Vukman在文献[2]中对2-非扰自由半素环R上的可加映射φ证明了，如果对于任意的a∈R，有2φ(a2)=φ(a)a+aφ(a)，那么φ是中心化子；Zalar在文献[3]中证明了2-非挠的半素环上的任意的左（右）Jordan中心化子是左（右）中心化子；Benkovič和Eremita在文献[4]中证明了2-非挠的素环上的可加映射φ，如果满足对任意的a∈R，n≥2都有φ(an)=φ(a)an-1，那么φ是左中心化子；Vukman在文献[5]中讨论了在标准算子代数Α上，若可加映射φ满足φ(am+n+1)=amφ(a)an（其中m，n为正整数），则存在数域F中的常数λ，使得对任意的a∈Α，有φ(a)=λa。Qi在文献[6]中将条件推广φ满足φ(am+n+1)-amφ(a)an∈FI（其中I为单位算子，F为实或复数域）即可。张等在文献[7]证明了在套代数上若可加映射φ满足φ(am+n+1)=amφ(a)an或(m+n)φ(ar+1)=mφ(a)ar+narφ(a)，则存在数域F中的常数λ，使得对任意的a∈Α，有φ(a)=λa。类似结果可见文献[8-10]。

三角代数首先是在文献[11]中引出，随后被许多学者所研究（见文献[8，11-15]）。设Α和B是作用在可交换环R上的代数，且分别含有单位元1Α和1B，M是忠实的含单位(Α，B)-双模。M称为忠实的Α-模是指如果a∈Α且aM=0，则有a=0。一个在通常矩阵算法意义下的R-代数：

称为三角代数。有关三角代数最典型，也是最重要的模型是上（下）三角矩阵代数和套代数。

设Z(T)为T的中心，由文献[11]中命题3可知：

显然，三角代数T是含单位I的，且存在非平凡幂等元e1和e2，其中：

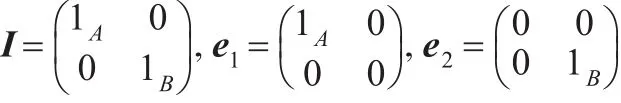
则由矩阵的运算可知，对于任意的1≤i≤j≤2，有Tij=eiTej。因而可以将三角代数T表示为：

这里，T11是T的子代数且同构于Α，T22是T的子代数且同构于B，T12是(T11，T22)-双模且同构于双模M。为了记述方便，用Tij来表示Α，M，B。

显然，三角代数是一类非半素的算子代数，并且受中心化子和中心化映射及上述结论的启发，自然想到在三角代数T上对于任意的a∈T，满足：(m+n)φ(ar+1)-(mφ(a)ar+narφ(a))∈Z(T)（其中m，n，r为正整数，Z(T)为T的中心）的可加映射φ的刻画。

2 满足条件 (m+n)φ(ar+1)-mφ(a)ar-narφ(a)∈Z(T)的映射

首先来讨论当r=1时的情形。

设φ:T→T是可加映射。如果存在正整数m，n≥1，使得：

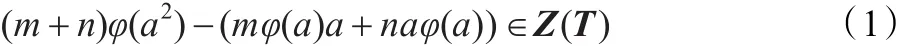
对所有的a∈T都成立。

引理2.1设φ是满足式（1）的可加映射，则对任意a，b∈T，有

证明（1）对于任意的a，b∈T，在式（1）中用a+b代替a可知：

又因为φ是可加映射，所以：

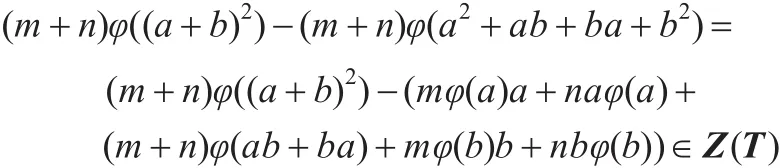
比较上两式可知（1）成立。

（2）在引理2.1中的（1）中取b=I易得（2）成立。

引理2.2设φ是满足式（1）的可加映射，则对1≤i≤j≤2，有φ(Tij)⊆Tij。

证明因为ei=e2i，所以存在Zei∈Z(T)，使得：

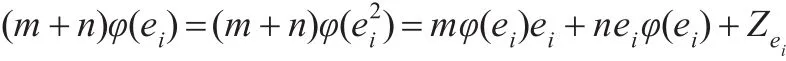
对上式两边同时左乘和右乘ei，可得Zei=0。因而：

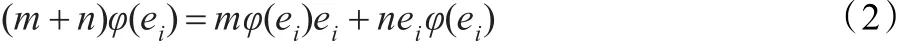
对式（2）分别左乘和右乘ei，得

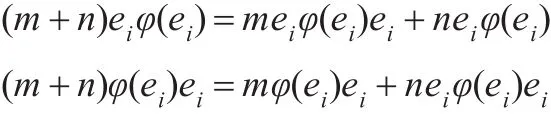
因而有φ(ei)=eiφ(ei)=φ(ei)ei=eiφ(ei)ei∈Tii。

另一方面，由引理2.1（2）知，存在∈Z(T)，使得：

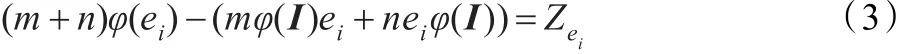
对式（3）两边分别左乘和右乘ei，得

上两式相减，则有：

对式（6）两边分别左乘和右乘ei，整理可得eiφ(I)=φ(I)ei=eiφ(I)ei。因而Zei=0。再由式（3）可知φ(ei)=φ(I)ei=eiφ(I)。对于任意的a11∈T11，由引理 2.1（2）可知，存在∈Z(T)，使得：

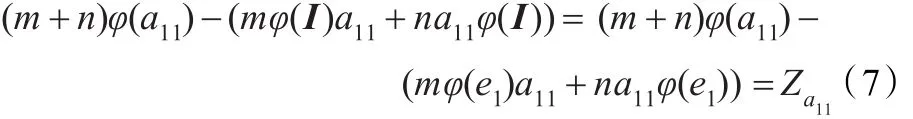
对式（7）两边同时左乘和右乘e1，得

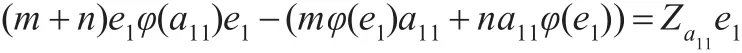
对式（7）两边同时左乘e1和右乘e2，得e1φ(a11)e2=0。

对式（7）两边同时左乘和右乘e2，得

由引理2.1（1），则存在∈Z(T)使得：

式（8）减式（7），得

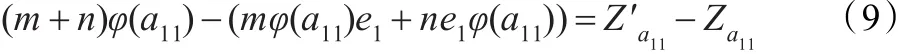
对式（9）两边同时左乘和右乘e1可得=Za11。此时，再对式（9）两边同时左乘和右乘e2，可得e2φ(a11)e2=0。故φ(a11)∈T11。

类似可以证明φ(a22)∈T22。

对于任意的a12∈T12，由引理2.1（1）可知，存在∈Z(T)使得：

由φ(ei)=φ(I)ei=eiφ(I)及引理2.1（2）可知，存在∈Z(T)使得：

由式（10）及式（11）可得：

对上式两边左乘e1，且由e1φ(a12)e1=φ(a12)e1可知Z′a12=

因而有：

对上式两边同时左乘和右乘e1，可得e1φ(a12)e1=0。对式（10）两边同时左乘和右乘e1及结合式（11），因而有：

再对上式两边同时左乘和右乘e2，得e2φ(a12)e2=0。于是φ(a12)=e1φ(a12)e2∈T12。于是引理2.2得到了证明。

引理2.3设φ是满足式（1）的可加映射，对于任意的aij，bij∈Tij(1≤i≤j≤2)，有

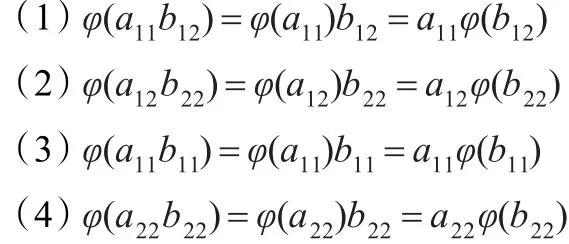
证明（1）对于任意的a11∈T11，b12∈T12，由引理2.1（1）及引理2.2可知存在∈Z(T)使得：

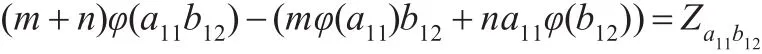
又由引理 2.2 可知φ(a11b12)，φ(a11)b12，a11φ(b12)∈T12，因此有=0。从而

利用类似的方法可得：

利用式（12）及引理2.2可知：

因此有：

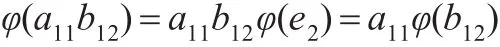
从而φ(a11b12)=φ(a11)b12=a11φ(b12)。从而结论（1）成立。

（2）由式（14）及式（15）可知

利用式（14）可得：φ(a12b22)=φ(a12)b22=a12φ(b22)。从而结论（2）成立。

（3）由结论（1），对任意的s12∈T12，有

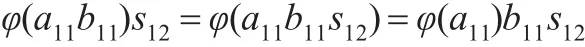
且φ(a11b11)s12=φ(a11b11s12)=a11φ(b11s12)=a11φ(b11)s12。

由引理2.3和引理2.1（1），则φ(a11b11)=φ(a11)b11=a11φ(b11)。从而结论（3）成立。

（4）由结论（2），对任意的s12∈T12，有s12φ(a22b22)=φ(s12a22b22)=s12a22φ(b22)且

由引理2.3和引理2.1（2）可知，φ(a22b22)=φ(a22)b22=a22φ(b22)。从而结论（4）成立。

定理2.1设T=Tri(Α，M，B)为三角代数，φ:T→T是一个可加映射。如果存在正整数m，n及对任意的a∈T都满足式（1），则存在λ∈Z(T)，使得对任意a∈T，有φ(Α)=λΑ。

证明设a，b∈T，则a=a11+a12+a22，b=b11+b12+b22，其中aij，bij∈Tij。由引理2.2和引理2.3得：

特别地，对任意a∈T，有φ(a)=φ(I)a=aφ(I)。因而存在λ∈Z(T)，使得φ(I)=λ，从而对任意a∈T，有φ(a)=λa。

定理2.2设T=Tri(Α，M，B)为三角代数，φ:T→T是一个可加映射。如果存在正整数m，n，r，使得对于任意的a∈T满足：

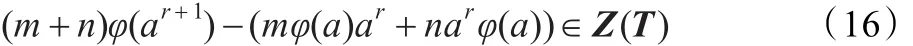
则存在λ∈Z(T)，使得对任意a∈T，有φ(a)=λa。

证明在式（16）中用a+tI代替a（t为任意正整数），且注意到φ(ta)=tφ(a)，则

在式（17）中依次取t=1，2，…，r，得到了一个以fi(a) (i=1，2，…，r)为变量的线性方程组：

此方程组的系数矩阵是范德蒙矩阵：

由式（19），则对任意a∈T，有：

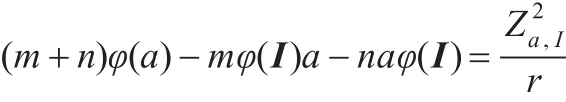
在上式中用a2代替a，得：

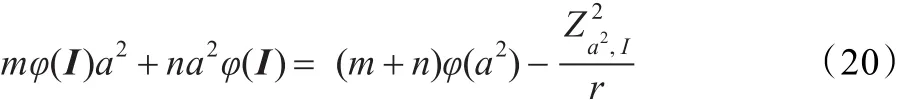
将式（20）代入式（18），化简得：

由定理2.1，则存在λ∈Z(T)，使得对任意a∈T，有φ(a)=λa。

通过定理2.2的证明过程，很容易得到下面的推论。

推论2.1设T=Tri(Α，M，B)为三角代数，φ:T→T是一个可加映射。则下面几个条件等价。

（1）存在λ∈Z(T)，使得对任意a∈T，有φ(a)=λa。

（2）存在正整数m，n，r，使得对任意的a∈T，有：(m+n)φ(ar+1)-(mφ(a)ar+narφ(a))∈Z(T)。

（3）对任意的正整数m，n，r和任意的a∈T，有：(m+n)φ(ar+1)-(mφ(a)ar+narφ(a))∈Z(T)。

（4）φ:T→T是中心化子。

3 结论

本文主要研究了三角代数上满足 (m+n)φ(ar+1)-(mφ(a)ar+narφ(a))在三角代数中心时的保持映射。有φ(a)=λa的固定形式，给出了三角代数上的保持映射的刻画，具有一定的理论意义。

[1]Brešar M.Centralizing mappings on von Neumann algebras[J]. Proc Amer Math Soc，1991，3：501-510.

[2]Vukman J，Kosi-Ulbl I.On centralizers of semiprime rings[J]. Aequationes Math，2003，66：277-283.

[3]Zalar B.On centralizers of semiprime rings[J].Comment Math Univ Carolin，1991，32：609-614.

[4]Benkovič D，Eremita D.Characterizing left centralizers by their action on a polynomial[J].Publ Math Debrecen，2004，64（3）：343-351.

[5]Vukman J，Kosiulbl I.Centralizers rings and algebras[J].Bull Austral Math Soc，2005，71：225-234.

[6]Qi X F，Du S P，Hou J C.Characterization of centralizers[J]. Acta Math Sinica，2008，51（3）：509-516.

[7]Yang C，Zhang J H.Generalized Jordan centralizers on nest algebras[J].Acta Math Sinica，2010，53（5）：975-980.

[8]Benkovič D，Eremita D.Commuting traces and commutativity preserving maps on triangular algebras[J].J Algebra，2004，280：797-824.

[9]Brešar M.On a generalization of the notion of centralizing mappings[J].Proc Amer Math Soc，1992，114：641-649.

[10]Brešar M.Centralizing mappings and derivations in prime rings[J].J Algebra，1993，156：385-394.

[11]Cheung W S.Commuting maps of triangular algebras[J].J London Mathematical Society，2001，63（1）：117-127.

[12]Chen L，Zhang J H.Nonlinear lie derivation on upper triangularmatrix algebras[J].Linearand MultilinearAlgebra，2008，56（6）：725-730.

[13]Benkovič D.Generalized lie derivations on triangular algebras[J].Linear Algebra Appl，2011，434（6）：1532-1544.

[14]Yu W Y，Zhang J H.Nonlinear lie derivations on triangular algebras[J].Linear Algebra Appl，2010，432（10）：2953-2960.

[15]Xiao Z K，Wei F.Jordan higher derivations on triangular algebras[J].Linear Algebra Appl，2010，432（10）：2615-2622.

MA Fei1，2,ZHANG Jianhua1,LI Li3,REN Ganglian2

1.College of Mathematics and Information Science,Shaanxi Normal University,Xi’an 710062,China
2.College of Mathematics and Information Science,Xianyang Normal University,Xianyang,Shaanxi 712000,China
3.School of Science,Xi’an Polytechnic University,Xi’an 710048,China

Τhis paper supposesTis a triangular algebra,andφ:T→Tis an additive mapping.It proves that if there is some positive integer numberm，n，rsatisfying(m+n)φ(ar+1)-mφ(a)ar-narφ(a)∈Z(T)for alla∈T,then there exists someλ∈Z(T),such thatφ(a)=λafor alla∈T.

additive map;centralizers;triangular algebras

设T是一个三角代数，φ:T→T是一个可加映射。证明了如果存在正整数m，n，r，使得(m+n)φ(ar+1)-(mφ(a)ar+narφ(a))∈Z(T)对任意的a∈T成立，那么存在λ∈Z(T)，使得对任意的a∈T，有φ(a)=λa。

可加映射；中心化子；三角代数

A

O177.2

10.3778/j.issn.1002-8331.1304-0135

MA Fei,ZHANG Jianhua,LI Li,et al.Characterization of centralizers on triangular algebras.Computer Engineering and Applications,2013,49（15）：23-26.

高等学校博士学科点专项科研基金（No.20110202110002）；陕西省教育厅研究计划资助项目（No.09JK803，No.2010JK890，No.11JK0469）；西安工程大学科研项目（No.BS1015）。

马飞（1981—），男，在读博士，讲师，研究领域为算子代数与自由概率；张建华（1965—），男，教授，博导，研究领域为算子代数与自由概率；李莉（1982—），女，博士，讲师，研究领域为算子理论与量子计算；任刚练（1970—），男，博士，副教授，研究领域为数论。E-mail：mafei6337@sina.com

2013-04-10

2013-05-28

1002-8331（2013）15-0023-04

◎理论研究、研发设计◎