动态分级中心引力约束优化算法及工程应用

吴华伟，陈特放

中南大学 信息科学与工程学院，长沙 410083

动态分级中心引力约束优化算法及工程应用

吴华伟，陈特放

中南大学 信息科学与工程学院，长沙 410083

1 引言

约束优化问题是科学研究与应用领域经常会遇到的一类数学规划问题，一个非线性约束优化问题通常可描述为：

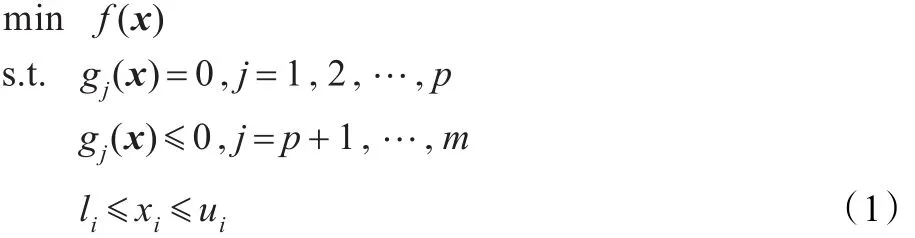
其中f(x)为目标函数，xi(i=1，2，…，n)为决策变量，gj(x)为约束条件，li和ui是变量xi取值的上下界。

智能优化算法具有不依赖于问题的梯度信息，利用种群对问题解空间进行多点并行搜索，能以较大概率收敛到问题的全局最优解等特点。结合合适的约束处理技术，目前智能优化算法已被广泛地应用于求解约束优化问题[1-2]。

中心引力优化（Central Force Optimization，CFO）算法是Formato最近提出的一种基于重力场粒子运动规律的智能优化算法[3]。CFO算法虽然具有原理简单，容易实现且具有较强的全局寻优能力。与其他基于种群迭代的智能优化算法一样，CFO算法同样具有后期收敛速度慢、易陷入局部最优的缺点。因此，研究者提出了许多的改进CFO算法。文献[4]提出了一种基于决策空间和决策变量自适应变化的中心引力优化算法用于求解大规模无约束优化问题。为了避免算法陷入局部最优。文献[5]将粒子的运动时间定义在适应度函数里，从而提出了一种自适应中心引力优化算法，该算法可以平衡其局部和全局搜索能力。文献[6]引入差分进化算子对当前粒子位置的分量进行变异，提出了一种基于差分进化算子变异的中心引力优化算法。

鉴于目前鲜有文献报道利用中心引力优化算法求解约束优化问题，本文利用非固定多段罚函数处理约束条件，设计出一种动态分级中心引力优化算法用于求解约束优化问题。几个典型的约束优化测试问题和工程优化问题的实验结果表明，该方法具有较好的优化性能。

2 中心引力优化算法

在描述CFO算法之前，先介绍一下与其相关的物理运动学知识。根据牛顿万有引力定律，任何两个物体之间的引力为：

式中，G为引力常量，m1和m2分别是两个物体的质量，r是两个物体之间的距离。物体m1作用于物体m2的加速度为：

式中，μ是物体m1和物体m2连线的单位向量，方向指向物体m2。假设在k时刻，物体的位置和速度分别为Xk和速度Vk，则在k+Dk时刻，物体的位置为：

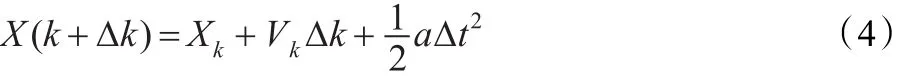
CFO算法是由Formato在2007年提出的一种基于物理运动学原理的群智能优化算法。它将优化问题解空间中的候选解当做带有质量的粒子，将目标函数f(X)定义粒子的适应度函数。假设所求问题的搜索空间为d维，在k时刻解空间里存在N个粒子2，…，N，在k时刻粒子Xi相对于粒子Xj的加速度为：

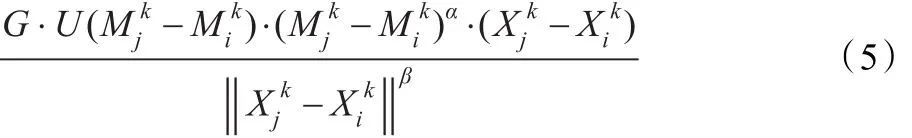
粒子Xi在k+1时刻的位置为：

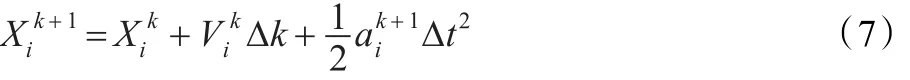
其中，是粒子Xi在k时刻的速度，通常取为0，Dk为时刻常数。

CFO算法的实现步骤如下：

步骤1在搜索空间中随机初始化粒子的加速度和位置。

步骤2计算每个粒子的适应度值。

步骤3判断算法是否满足终止条件，若满足，则算法结束，输出最优解；否则执行步骤4。

步骤4根据式（6）和式（7）更新每个粒子的加速度和位置，返回步骤2。

3 动态分级约束优化CFO算法

3.1 算法思想

针对CFO算法具有种群多样性差、对种群的初始分布要求较高、全局搜索能力不强等缺点[7]，本文提出一种动态分级的约束优化CFO算法，其思路主要为：首先利用佳点集方法构建初始种群，以保证粒子能均匀分布在搜索空间中。将种群分为2个子种群，其粒子数目分别为N1和N2，满足N1+N2=N，N为种群规模。在每次迭代后，将适应度值较优的N1个粒子作为第1个子种群，引入模式搜索方法[8]用于进行局部搜索；将适应度值较差的N2个粒子作为第2个子种群，引入多样性变异算子[9]以增强算法的全局搜索能力。在迭代过程中，进化的初始阶段应偏重于全局搜索，因而此阶段的N2值应取较大些，以增强算法的全局搜索能力；进化的末期，主要考虑局部精确搜索，这时N1的取值应大些，以提高算法的局部搜索能力。因此，在每次迭代过程中两个子种群的粒子数目是自适应动态调整的。

3.2 种群初始化

由于CFO算法是一种基于种群迭代的群智能搜索方法，因此初始种群的优劣对算法的搜索性能具有较大的影响。若群体中粒子在搜索空间中分布不均匀，则可能导致算法的搜索效率及搜索能力受到一定的限制。佳点集方法是一种均匀取点的实验方法，其偏差仅为O(n-1+ε)，其中n为取点个数，ε为无穷小量。具体取点方法详见文献[10]。本文采用佳点集方法来产生初始种群。图1是采用佳点集方法产生的规模为80的初始种群分布，其中，变量的维数为2，变量的取值范围为[-20，20]。

从图1可以清楚地看出，与随机方法相比，佳点集方法产生的初始粒子分布均匀，具有较好的多样性。

图1 佳点集方法产生的80个初始种群分布

3.3 模式搜索法

模式搜索法是由Hooke等[8]提出的一种有效的确定性直接搜索方法，具有较强的局部搜索能力，其具体步骤如下：

（1）给定初始点x(1)∈Rn，n个轴向坐标方向为e1，e2，…，en，初始步长δ，加速因子μ≥1，缩减率ω∈[0，1]，允许误差为ε＞0，令y(1)=x(1)，k=1，j=1。

（2）对每个分量依次进行轴向搜索(j=1，2，…，n)，若f(y(j)+δej)优于f(y(1))，y(j+1)=y(j)+δej；若f(y(j)-δej)优于f(y(1))，y(j+1)=y(j)-δej；否则y(j+1)=y(j)。

（3）若f(y(n+1))优于f(x(k))，置x(k+1)=y(n+1)，令y(1)=x(k+1)+μ(x(k+1)-x(k))，k=k+1，j=1，转步骤（2），否则进行步骤（4）。

（4）若δ≤ε，则迭代停止，得点x(k)；否则δ=ωδ，y(1)=x(k)，x(k+1)=x(k)，k=k+1，j=1，转步骤（2）。

3.4 多样性变异算子

为了增加种群多样性，本文对第1个子种群进行多样性变异，具体操作如下[9]：

假设群体中粒子Xi表示为Xi=(xi1，xi2，…，xid)，以概率1/n随机从粒子Xi中选择一个元xih(h=1，2，…，d)，然后在[li，ui]中随机产生一个实数替代粒子Xi中选择一个元xih，从而产生新的个体X′i=(x′i1，x′i2，…，x′id)。多样性变异算子为：

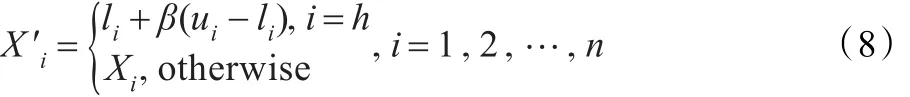
式中，β∈U[0，1]。

3.5 约束处理技术

如何处理好约束条件是利用进化算法求解约束优化问题的关键。

对于如式（1）所示的约束优化问题，通常所构造的广义目标函数具有如下形式：

其中f(x)为原目标函数，δ(t)H(x)称为惩罚项，δ(t)表示惩罚力度，H(x)为惩罚因子。

Parsopoulos等[11]提出了一种基于非固定多段映射罚函数法的约束优化粒子群算法。本文也采用非固定多段映射罚函数法处理约束条件，在文献[11]的基础上，并对其进行适当修正。设

其中，式（11）表示对约束的违反程度，式（12）表示惩罚函数的强度，式（13）为分段映射函数，式（14）为随迭代次数变化的惩罚力度。这样可根据约束违反程度的大小，自适应选取不同的惩罚力度，将约束优化问题转化为一系列无约束优化问题来处理，可以避免采用精确罚函数法中惩罚因子难以选取的问题[11]。

3.6 算法步骤

步骤1设置算法参数。初始化种群规模，在每个变量的定义域内，利用佳点集方法产生初始种群。

步骤2按式（11）～（13）分别计算各粒子每个约束条件的惩罚因子。

步骤3按式（10）分别计算每个粒子的所有约束条件的惩罚因子H(x)。

步骤4根据式（9）计算出每个粒子的适应度值，求出最优适应度值及最优粒子。

步骤5判断惩罚因子H(x)是否达到精度要求或是否达到最大迭代次数，若是则退出，否则执行步骤6。

步骤6将种群分为两个子种群，第1子种群引入模式搜索，第2子种群嵌入多样性变异算子，按式（6）和式（7）更新粒子的加速度和位置，返回步骤2。

4 数值实验

为了评估本文算法的性能，从文献[1]中选取4个标准测试问题，即g01、g02、g06和g11进行测试，各问题的具体表达式详见文献[1]。将本文算法记为DHCFO，并与SR算法[1]、SMES算法[2]、HEA-ACΤ算法[9]、COHEA算法[10]和CPSO算法[12]得到的结果进行了比较。实验中，DHCFO算法的参数设置为：种群规模N=100，G=2，α=0.3，β=0.5，Dt=1，模式搜索法中的δ=2.0，μ=1.0，ω=0.1，ε=0.1。问题g01、g06和g11的迭代次数为1 000，g02的迭代次数为3 000。其他算法的参数设置分别见其各自的文献。每个测试问题在相同条件下独立运行20次实验，记录其最好结果、平均结果、最差结果和标准差。表1给出了在上述参数设置下，五种算法对4个标准测试问题的寻优结果比较。

从表1中的结果可知，除g02外，DHCFO算法对其他3个问题20次实验中一致地找到全局最优解。与SR算法相比，DHCFO算法在问题g02和g06的平均结果和最差结果方面明显优于SR算法，最优结果和标准差相当。对于问题g01和g11，DHCFO算法取得了与SR算法相似的结果。与SMES算法相比，DHCFO算法在问题g01、g06和g11上的最优结果、平均结果和最差结果方面均占优，对于g02，DHCFO算法的平均值、最差值要优，SMES得到了较好的最优值。与HEA-ACΤ算法相比，DHCFO算法在4个问题上得到了相似的结果。与COHEA算法相比，DHCFO算法在问题g01、g06和g11上得到了相似的结果，在问题g02上得到的结果要优。与CPSO算法相比，DHCFO算法在问题g02上的最优结果、平均结果和最差结果方面稍差，对于问题g01、g06和g11，两种算法取得了相似的结果。

图2（a）～（d）给出了4个问题的寻优曲线。从图2（a）～（d）中的收敛曲线可知，DHCFO算法能快速地收敛于问题的全局最优解或近似全局最优解。从以上比较研究可以看出，DHCFO算法表现出良好的寻优性能。

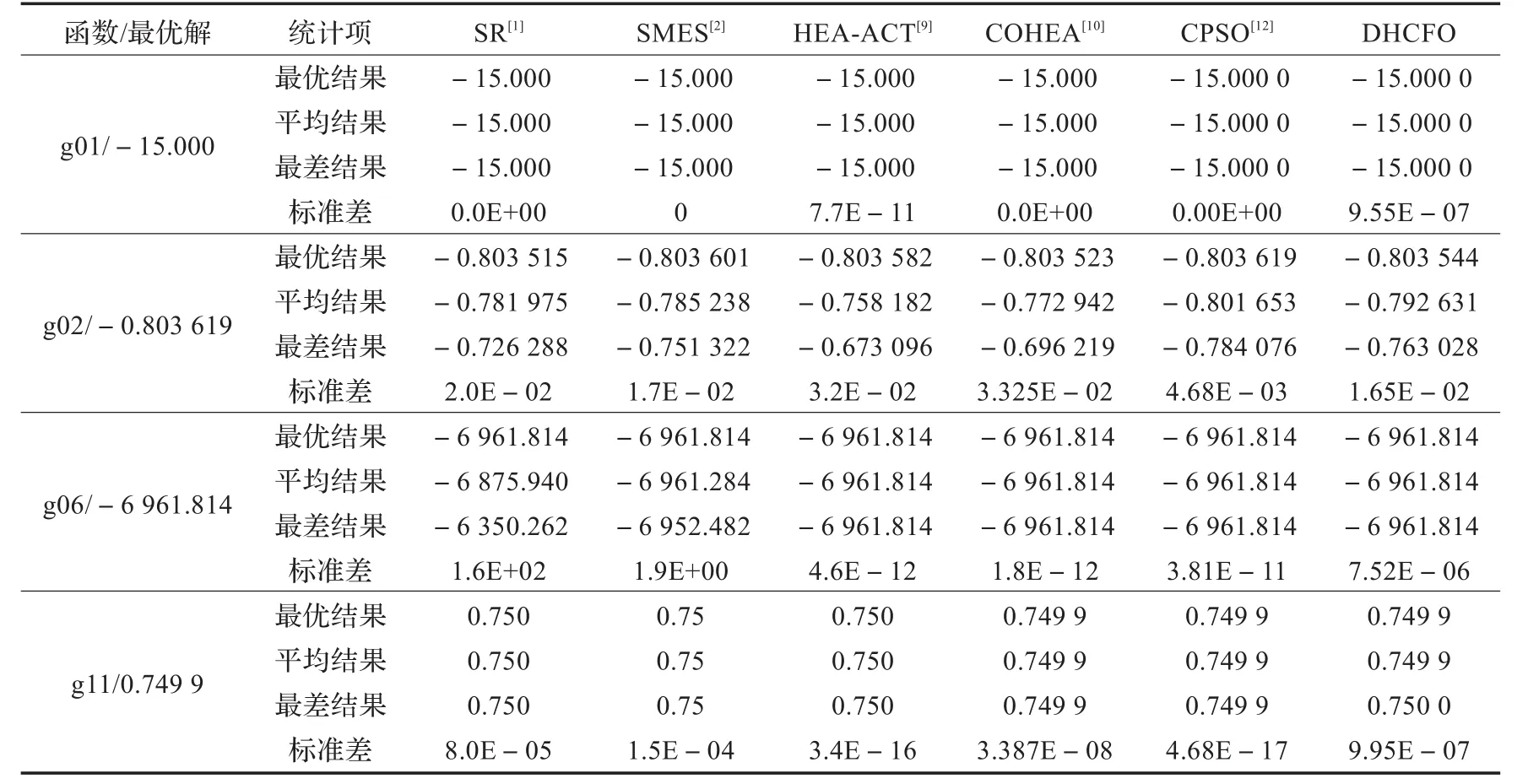
表1 六种算法对4个问题的实验结果比较

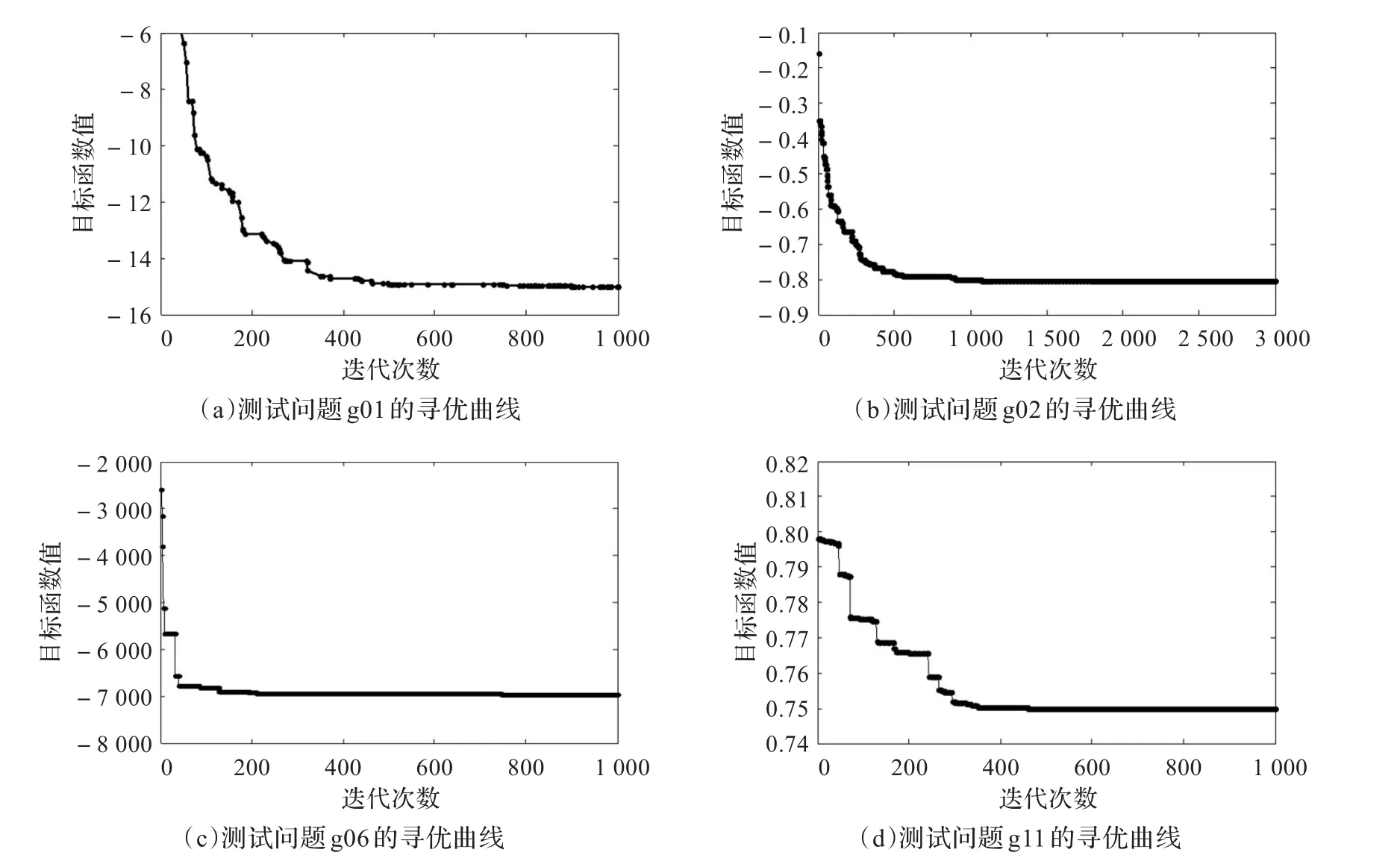
图2 测试函数g01、g02、g06和g11的寻优曲线

5 DHCFO在焊接梁优化中的应用

为了进一步验证DHCFO算法的有效性，将其应用到焊接梁优化设计问题中。

图3 焊接梁优化设计问题

焊接梁优化设计问题[13]如图3所示。在图3中，设计变量分别为h（记为x1），l（记为x2），t（记为x3）和b（记为x4）。约束条件分别为剪应力约束g1(x)；梁上弯曲应力约束g2(x)；边界约束为g3(x)，g4(x)和g5(x)；梁的尾端误差约束g6(x)；g7(x)表示载荷P的约束。

利用DHCFO算法对焊接梁优化设计问题进行求解，并与文献[9]中的HEA-ACΤ算法、SC算法、FSA算法、文献[13]中的GA算法、NMHA算法、NMDE算法、文献[14]中的DSS-MDE算法和文献[15]中的IPSO算法进行比较，结果如表2所示。从表2中的结果可知，DHCFO算法要优于文献中其他方法。

表2 几种算法对焊接梁优化设计问题的结果比较

6 结论

提出一种动态分级中心引力优化算法用于求解约束优化问题。针对中心引力优化算法存在的问题，该算法利用佳点集方法构造初始种群以保证粒子的多样性，将种群分为两个子种群，分别进行局部搜索和全局搜索，并动态调整子种群粒子的数目。几个标准测试函数和工程应用的实验结果表明该算法具有较好的寻优效果。

[1]Runarsson Τ P，Yao X.Stochastic ranking for constrained evolutionary optimization[J].IEEE Τransactions on Evolutionary Computation，2000，4（3）：561-579.

[2]Mezura-Montes E，Coello C A C.A simple multi-membered evolution strategy to solve constrained optimization problems[J].IEEE Τransactions on Evolutionary Computation，2005，9（1）：1-17.

[3]Formato R A.Central force optimization：a new metaheuristic with applications in applied electromagnetics[J].Progress in Electromagnetics Research，2007，77：425-491.

[4]Formato R A.Central force optimization with variable initial probes and adaptive decision space[J].Applied Mathematics and Computation，2011，217（21）：8866-8872.

[5]钱伟懿，张桐桐.自适应中心引力优化算法[J].计算机科学，2012，39（6）：207-209.

[6]张桐桐，卢静，钱伟懿.基于差分进化算子变异的中心引力优化算法[J].渤海大学学报：自然科学版，2012，33（3）：197-203.

[7]谢丽萍，曾建潮.受拟态物理学启发的全局优化算法[J].系统工程理论与实践，2010，30（12）：2276-2282.

[8]Hooke R，Jeeves Τ A.Direct search solution of numerical and statistical problems[J].Journal of the Association for Computing Machinery，1961，8（2）：212-229.

[9]Wang Y，Cai Z X，Zhou Y R，et al.Constrained optimization based on hybrid evolutionary algorithm and adaptive constraint-handling technique[J].Structuraland Multidisciplinary Optimization，2009，37（1）：395-413.

[10]龙文，梁昔明，徐松金，等.聚类佳点集交叉的约束优化混合进化算法[J].计算机研究与发展，2012，49（8）：1753-1761.

[11]Parsopoulos K E，Vrahatis M N.Particle swarm optimization method for constrained optimization problems[C]//Proc of the Euro-International Symposium on Computational Intelligence，2002：214-220.

[12]Daneshyari M，Yen G G.Constrained multiple-swarm particle swarm optimization within a cultural framework[J].IEEE Τransactions on Systems，Man，and Cybernetics，2012，42（2）：475-490.

[13]Zou D X，Liu H K，Gao L Q，et al.A novel modified differential evolution algorithm for constrained optimization problems[J].Computers and Mathematics with Applications，2011，61（6）：1608-1623.

[14]Zhang M，Luo W J，Wang X F.Differential evolution with dynamic stochastic selection for constrained optimization[J]. Information Sciences，2008，178（15）：3043-3074.

[15]He S，Prempain E，Wu Q H.An improved particle swarm optimizer for mechanical design optimization problems[J]. Engineering Optimization，2004，36（5）：585-605.

WU Huawei,CHEN Τefang

School of Information Science and Engineering,Central South University,Changsha 410083,China

Using non-stationary multi-stage penalty function to deal with the constrained conditions,a modified central force optimization algorithm is proposed for solving constrained optimization problems.Good point set method is used in the initialization of the evolutionary population to ensure its diversity.At each generation,the population is divided into two subpopulations based on the fitness values of particles,which is employed for global and local search respectively.Τhe number of the subpopulation is dynamically adapted according to the search phases.Τhe proposed algorithm has been tested on 4 benchmark problems and engineering optimization problems,and the results show that it can deal with different constrained optimization problems.

constrained optimization problems;central force optimization algorithm;non-stationary multi-stage penalty function; engineering optimization

结合非固定多段罚函数处理约束条件，提出一种动态分级中心引力优化算法用于求解约束优化问题。该算法利用佳点集初始化个体以保证种群的多样性。在每次迭代过程中将种群分为两个子种群，分别用于全局搜索和局部搜索，根据搜索阶段动态调整子种群个体数目。对几个标准的测试问题和工程优化问题进行数值实验，结果表明该算法能处理不同的约束优化问题。

约束优化问题；中心引力优化算法；非固定多段罚函数；工程优化

A

ΤP301.6

10.3778/j.issn.1002-8331.1212-0190

WU Huawei,CHEN Tefang.Central force constrained optimization algorithm with dynamic hierarchical and engineering application.Computer Engineering and Applications,2013,49（15）：14-18.

国家863重点项目（No.2009AA034302）。

吴华伟（1979—），男，博士研究生，主要研究领域为进化计算、智能控制等；陈特放（1957—），男，教授，博士生导师，主要研究领域为机车车辆故障诊断、智能交通系统等。

2012-12-17

2013-05-02

1002-8331（2013）15-0014-05

CNKI出版日期：2013-05-15 http://www.cnki.net/kcms/detail/11.2127.ΤP.20130515.1015.007.html