SVM-HDMR高维非线性近似模型构造法

李 亮，孙 秦

西北工业大学 航空学院，西安 710072

SVM-HDMR高维非线性近似模型构造法

李 亮，孙 秦

西北工业大学 航空学院，西安 710072

1 引言

近似模型是利用科学或工程系统已有的输入和输出数据构造的用于表示系统输入和输出关系的数学模型。例如，在工程优化设计中，构造近似模型代替物理试验或数值分析，可以有效提高优化设计的效率。

目前国内外已经发展了多种近似模型构造法，主要有移动最小二乘法（MLS）[1]，多项式响应面法（PRS）[2]，人工神经网络（ANN）[3]，径向基函数网络（RBF）[4]，克里格法（Kriging）[5]以及支持向量机（SVM）[6]等。通过调查，发现这些近似模型构造法已成功应用于多种学科的低维问题中。但是随着维数的增加，用于构造这些近似模型的样本数量和计算成本会急剧增加，尤其是对样本值获取比较耗时的问题，往往因计算量过大而无法承担，形成所谓的“维数灾难”。

为了构造高维下的近似模型，Sobol[7]提出了HDMR近似模型构造法，利用函数的层级属性，采用分而治之的思想，将高维问题分解为一系列低维问题进行求解，从而大大提高了计算效率。到目前，HDMR已经发展出多种形式，其中以Rabitz[8]提出的Cut-HDMR最为简单实用。为了求解Cut-HDMR中的各阶低维问题，Shan[9]提出了基于RBF的Cut-HDMR，后来Wang和Τang[10-11]又提出了基于MLS和Kriging的Cut-HDMR。

本文在前人的工作基础上，将 LS-SVM引入Cut-HDMR，提出了SVM-HDMR，并建立了一套自适应的采样和模型构造算法，以保证使用尽可能少的样本点获得尽可能高的近似精度。

2 Cut-HDMR基本理论

HDMR可以有效地表示出科学或工程系统中输入变量与输出响应间的映射关系，其一般形式为[7]：

式中，x=[x1，x2，…，xn]Τ为输入变量，f(x)为输出响应。等式右边各项被称为组件函数，其中f0是常数项，用以表示对响应的零阶效应；fi(xi)表示变量xi独立对响应产生的效应，即一阶效应，它与xi可能成线性关系或非线性关系；fij(xi，xj)表示变量xi和xj耦合作用对响应产生的效应，即二阶效应，它与xi和xj也可能成线性关系或非线性关系。后面的各项表示了数目依次增加的变量耦合作用对响应产生的效应。最后一项表示所有变量耦合作用对响应产生的效应。

用HDMR构造近似模型的关键是对各阶组件函数的求取，一般做法是构造相应阶数的近似函数对其进行近似。本文采用的Cut-HDMR在变量空间中选取一个点x0作为切割中心，通过将f(x)在通过切割中心的直线、平面以及超平面上的值进行叠加来表示f(x)。Cut-HDMR的各阶组件函数如下列各式所示[8]：

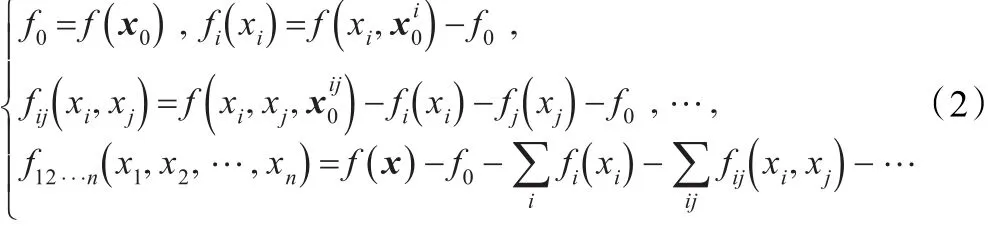
式中，表示没有xi的x0，表示没有xi和xj的x0。x0、和分别是零阶、一阶和二阶组件函数的构造点。

3 LS-SVM

LS-SVM[12-13]是对标准SVM的发展，是一种有效的非线性近似模型构造法。它以二次损失函数为经验风险，用等式约束代替不等式约束，根据结构风险最小化原则，将近似模型的构造转化为如下优化问题：

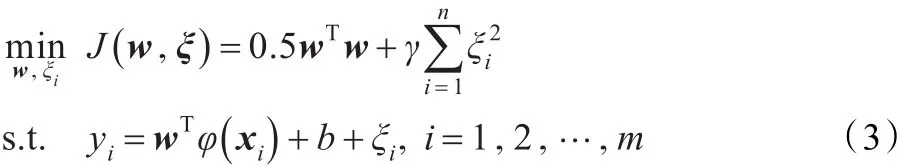
式中，w和b为模型参数，γ为正则化参数，ξi为误差函数。引入拉格朗日乘子α=[α1，α2，…，αm]Τ，得到如下拉格朗日函数：

式中，y=[y1，y2，…，ym]Τ为样本值集合，1=[1 ，…，1]Τ，K=为核函数，I为单位阵。解线性方程组（5）求得b和α，得到如下回归函数：

4 SVM-HDMR近似模型构造法

在一般工程问题中，低阶项对响应的效应都较强，随着阶数增加，相应组件函数对响应的效应逐渐减弱[9]。为了尽量减少计算成本，本文提出的SVM-HDMR算法只考虑到二阶项，其形式为：

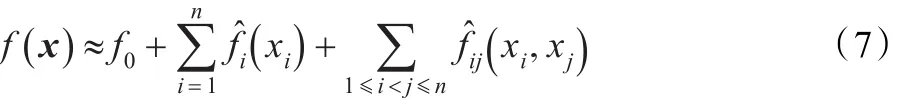
为了提高样本利用率和降低计算成本，本文采用了自适应采样法。与传统的按照一定算法一次性采集大量甚至所有所需样本点的方法相比，自适应采样法根据需要按照一定算法每次只采集一个或多个样本点，提高了采样的针对性，以最大限度地减少所需样本总数。SVM-HDMR的自适应采样和模型构造算法如下：

（1）在变量空间的中心附近随机选取一个点x0= [x10，x20，…，]Τ作为切割中心，并求出该点处的响应值f0=f(x0)。对于一般工程问题，如果展开式（1）收敛，则插值效果与中心位置的选取无关[9]。

（2）在变量xi取值范围的上界和下界的邻域内各随机选取一个值作为变量xi的值，其余n-1个变量的值都与x0保持一致，得到两个样本点和。这里的邻域指的是在设计空间中沿xi方向离一个设计点的距离不超过xi取值范围的1%。求出这两个点处的响应值，得到一阶组件函数fi(xi)在下界点的值fi(xiL)=f(xiL，)-f0和在上界点的值fi(xiU)=f(xiU，)-f0。在这两个点上作线性插值构造近似一阶组件函数。

（3）对fi(xi)的线性与否进行校核。如果过点x0，即若，可认为fi(xi)是线性的，则的构造结束；否则，认为fi(xi)是非线性的，则用LS-SVM在点x0及步骤（2）中采集的两个点上重新构造然后沿xi方向在xi取值范围内随机取一个数作为变量xi的值，其余n-1个变量的值仍与x0保持一致，得到一个新点。求该点处的响应值，并求重新构造的在该点处的相对误差。如果相对误差小于给定的阀值（如0.1），则的构造结束；否则，用LS-SVM在这个新点与之前的三个点处再次重新构造。重复这个过程，直到得到足够精确的为止。

（4）反复执行步骤（2）和步骤（3），直到得到所有近似一阶组件函数。

（5）在变量空间中取一个新点，该点每一维的值都是从该维在步骤（2）和步骤（3）中所取过的值中随机抽出的。求出这个新点处的响应值和一阶近似值，若两个值的相对误差小于某个阀值（如0.001），则认为不存在二阶项，模型构造结束；否则，转到步骤（6）。

（6）在变量空间中取一个新点，该点中变量xi和xj(i≠j)的取值都是相应维在步骤（2）和步骤（3）中所取过的值中随机抽出的，其余各维的值都与x0保持一致。求出该点处的响应值和一阶近似值。若两个值的相对误差小于某个阀值（如0.001），则认为变量xi和xj间无耦合效应或两个变量间的耦合效应对响应所起的作用可忽略不计；否则，用LS-SVM在该点及步骤（2）和步骤（3）中针对变量xi和xj所采集的点上构造。然后，如同取上一个点的方式，再取一个新点，并求该点处的响应值和二阶近似值，若两个值的误差小于某个阀值（如0.1），则的构造结束；否则，用LS-SVM在这个新点及之前用过的点上再次重新构造。重复这个过程，直到得到足够精确的为止。

（7）反复执行步骤（6），直到得到所有的近似二阶组件函数。

5 数值算例

为了验证SVM-HDMR算法的计算效率和近似精度，用Fortran语言编写了计算程序和测试程序，并用该算法求解了三个函数算例和一个工程算例。

5.1 评价指标

为了校核构造的近似模型与真实响应函数的误差大小，采用了如下两种误差评价指标：

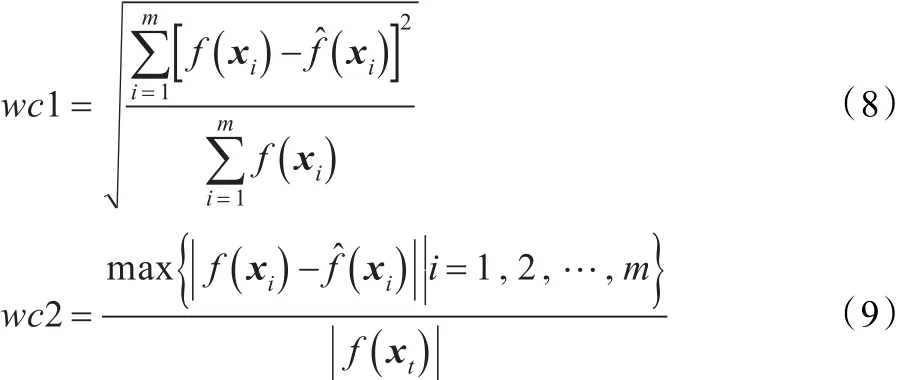
其中，xi(i=1，2，…，m)是在变量空间中随机生成的m个服从均匀分布的测试样本点，xt是测试样本集中与对应的样本点。wc1和wc2分别从整体上和局部区域上反映近似模型的精度，两者都是越接近于0，则近似模型的精度越高。

5.2 函数算例

考虑如下三个测试函数：

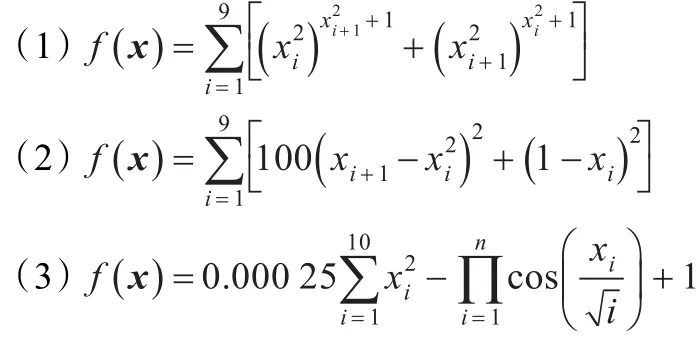
这三个函数均为10维，变量的取值范围均取为[0 ，2]。分别用MLS-HDMR[10]、Kriging-HDMR[11]以及SVM-HDMR构造这三个函数的近似模型。取测试样本点个数为5 000，测试结果如表1所示。

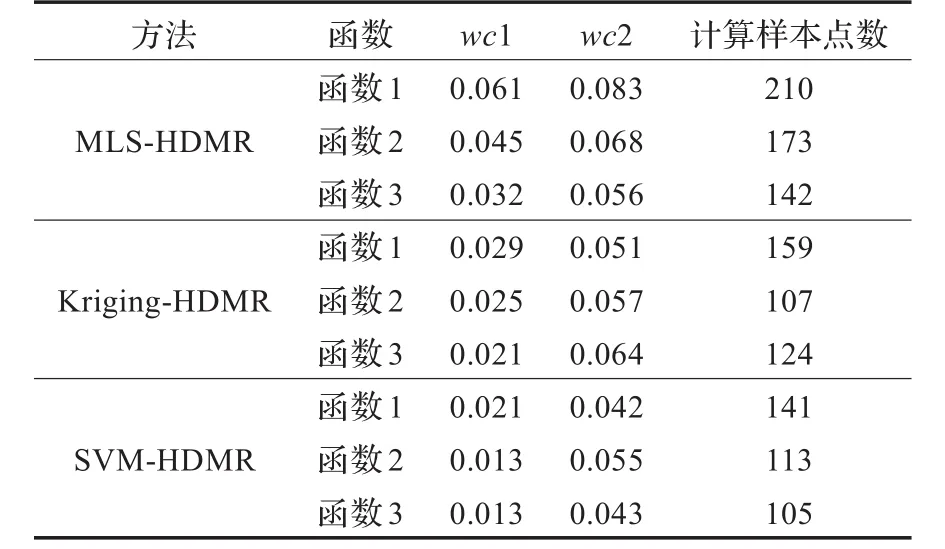
表1 函数算例测试结果

从表1中数据可知，用SVM-HDMR对三个测试函数构造的近似模型都有较好的近似精度，所用的计算样本点数也较少。如果用LS-SVM构造10维函数的近似模型，若用全析因法采样，每维取三个水平，则所需样本点数为59 049个。可见，与传统近似方法相比，SVM-HDMR极大地降低了构造近似模型的计算成本。

从表1还可以看到，SVM-HDMR对三个测试函数构造的近似模型的近似精度均高于MLS-HDMR和Kriging-HDMR，且所用的计算样本点也更少。

5.3 工程算例

考虑一个如图1所示的飞机平尾结构有限元模型，将翼根固支，在上、下蒙皮施加气动载荷。分别将平尾的上蒙皮和下蒙皮沿展向分为9段，将每一段的蒙皮厚度设为一个变量，一共有18个变量。

图1 飞机平尾结构有限元模型

采用NASΤRAN求解器对该模型进行有限元分析，用SVM-HDMR构造近似模型来近似翼尖挠度与18个厚度变量间的函数关系。取测试样本点个数为500，测试结果如表2所示。

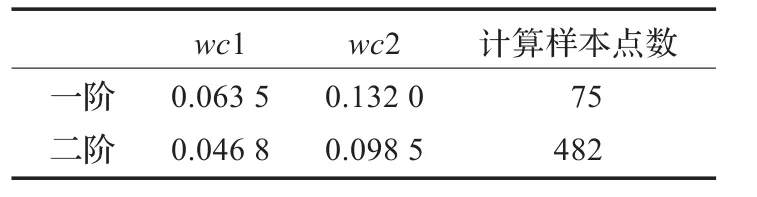
表2 工程算例测试结果

表2中的“一阶”表示只求解SVM-HDMR的常数项和一阶项，“二阶”表示还要求解二阶项。从表2中数据可知，用一阶和二阶SVM-HDMR构造的近似模型都具有较好的近似精度。二阶近似与一阶近似相比，其近似精度只有较小的改进，但所用的计算样本点数却增加较大。近似精度的改进较小是因为在某些工程问题中，虽然二阶及更高阶的耦合效应存在，但是与零阶效应和一阶效应相比，所占的比重较小。在工程问题中对样本点求值比较耗时，如果只考虑到一阶项就能取得较好的近似精度，就显著地降低了计算成本。尤其是对于超高维问题，如维数达到1 000时，二阶组件函数的数量为499 500，求解这些组件函数所需的样本点数会达到上百万，这对于工程计算几乎是不可能实现的。而如果只考虑到一阶项，对于一个一千维的问题，只需要求1 000个一阶组件函数即可，若以每维取5个样本点为例，一共只需要采集4 001个样本点。但是，具体在哪些工程问题中只考虑到一阶项就能取得较好的近似精度，还需要在以后进一步的研究中以及实际应用中进行测试和鉴别。

6 结论

为了构造高维下的近似模型，本文在前人工作的基础上，将 LS-SVM引入 Cut-HDMR，提出了SVM-HDMR高维非线性近似模型构造法。该方法利用Cut-HDMR将高维问题转化为一系列低维问题，再用LS-SVM求解这些低维问题。为了提高样本利用率和降低计算成本，本文提出了一套完整的自适应采样和模型构造算法。该算法按照设计变量的先后顺序，从低阶到高阶依次构造各阶组件函数，所用的计算样本点都是根据误差阀值的判断并依据一定的规则一个一个选取出来的。这与传统的按一定算法一次性采集大量甚至所有所需样本点的做法相比，提高了采样的目的性和样本点的利用率。另外，与传统近似方法只利用了样本信息相比，该算法还利用了函数自身的层级属性，增加了构造近似模型所用的信息量。

数值算例的测试结果表明该方法具有较好的近似精度，且与传统近似方法相比极大地降低了计算成本，从而更适用于高维工程问题的求解。测试结果还表明，本文方法与MLS-HDMR以及Kriging-HDMR相比，具有更高的近似精度，且所用的计算样本点也更少。对于某些工程问题，只考虑到SVM-HDMR的一阶项就能取得较好的近似精度，从而进一步降低了计算成本。因此，该方法在超高维问题中也具有很好的应用前景，如在大规模结构的全局优化中，用该方法构造设计目标及约束响应与设计变量间的近似函数关系，再用优化算法对这些近似函数进行全局搜索，从而找到全局最优点作为原结构优化问题的全局最优点。在实际应用中，哪些工程问题只需要考虑到一阶项就能取得较好的近似精度，还有待进一步研究。

本文采用近似方法估算LS-SVM的核参数σ，并将正则化参数γ近似取为+∞。为了使SVM-HDMR方法具有更好的稳健性，在进一步的研究中有待考虑将这些参数的优化算法结合到本文的算法中。

[1]Lancaster P，Salkauskas K.Surfaces generated by moving least squares methods[J].Mathematics of Computation，1981，37（155）：141-158.

[2]Box G E P，Wilson K B.On the experimental attainment of optimum condition[J].Journal of the Royal Statistical Society，1951，13（1）：1-45.

[3]Swinger K.Applying neural networks，a practical guide[M]. [S.l.]：Morgan Kaufmann Publishing Inc.，1996：3-21.

[4]Mulgrew B.Applying radial basis functions[J].IEEE SP Magazine，1996，13（2）：50-65.

[5]Sacks J，Welch W J，Mitchell Τ J，et al.Design and analysis of computer experiments[J].Statistical Science，1989，4（4）：409-435.

[6]Cortes C，Vapnik V.Support vector networks[J].Machine Learning，1995，20（3）：273-297.

[7]Sobol I M.Sensitivity estimates for nonlinear mathematical models[J].Mathematical Modeling&Computational Experiment，1993，1（4）：407-414.

[8]Rabitz H，Alls Ö F.General foundations of high-dimensional model representations[J].Journal of Mathematical Chemistry，1999，25（2/3）：197-233.

[9]Shan S Q，Wang G G.Metamodeling for high dimensional simulation-based design problems[J].JournalofMechanical Design，2010，132（5）.

[10]Wang H，Τang L，Li G Y.Adaptive MIS-HDMR metamodeling techniques for high dimensional problems[J].Expert Systems with Applications，2011，38（11）：14117-14126.

[11]汤龙，李光耀，王琥.Kriging-HDMR非线性近似模型方法[J].力学学报，2011，43（4）：780-784.

[12]Suykens J A K，Vandewalle J.Least squares support vector machine classifiers[J].Neural Processing Letters，1999，9（3）：293-300.

[13]Gestel Τ V，Suykens J A K，Baesens B，et al.Benchmarking least squares support vector machine classifiers[J].Machine Learning，2004，54（1）：5-32.

LI Liang,SUN Qin

School of Aviation,Northwestern Polytechnic University,Xi’an 710072,China

In order to construct approximation model for high dimensional problems,Least Squares Support Vector Machine（LS-SVM）is introduced into High Dimensional Model Representation（HDMR）,and a modified approximation model construction method called SVM-HDMR for high dimensional nonlinear problems and corresponding adaptive sampling and model construction algorithm are proposed.Τhis method transforms high dimensional problem into a series of low dimensional problems using Cut-HDMR,and then these low dimensional problems are solved using LS-SVM.Τhe results of numerical examples show that the new method has good approximation quality and reduces computational expense dramatically,so it is more suitable for high dimensional problems.

approximation model;Least Squares Support Vector Machine（LS-SVM）;Cut-High Dimensional Model Representation（HDMR）;adaptive sampling

为了构造高维下的近似模型，将最小二乘支持向量机（LS-SVM）引入切割高维模型表示（Cut-HDMR），提出了SVM-HDMR高维非线性近似模型构造法，给出了相应的自适应采样和模型构造算法。该方法利用Cut-HDMR将高维问题转化为一系列低维问题，用LS-SVM求解这些低维问题。数值算例的测试结果表明该方法具有较好的近似精度，且与传统近似方法相比极大地降低了计算成本，从而更适用于高维工程问题的求解。

近似模型；最小二乘支持向量机（LS-SVM）；切割高维模型表示（Cut-HDMR）；自适应采样

A

O241.3

10.3778/j.issn.1002-8331.1301-0115

LI Liang,SUN Qin.SVM-HDMR approximation model construction method for high dimensional nonlinear problems. Computer Engineering and Applications,2013,49（15）：6-9.

中航工业产学研创新项目（No.Cxy2010xG18）。

李亮（1984—），男，博士研究生，主要研究领域为飞行器结构设计；孙秦（1956—），男，博士，教授，博士生导师，主要研究领域为飞行器结构设计。E-mail：gafeiad@163.com

2013-01-11

2013-04-15

1002-8331（2013）15-0006-04