现代化战争条件下的兰切斯特战斗模型

占栋辉，陈 刚，张宏军，郝文宁，冯 波

解放军理工大学 工程兵工程学院，南京 210007

现代化战争条件下的兰切斯特战斗模型

占栋辉，陈 刚，张宏军，郝文宁，冯 波

解放军理工大学 工程兵工程学院，南京 210007

兰切斯特方程式是在1914年由运筹学家兰切斯特所提出，起初这个方程式是一个简单的微分方程，主要是用于描述部队兵力对峙的变化情形[1-2]。在经典的兰切斯特方程式中用B，R代表作战双方兵力，假设B(t)和R(t)分别代表t时刻蓝方和红方这两支部队的参战兵力，兰切斯特方程为式（1）[3]。在不考虑自然损耗和兵力补给的条件下，方程组（1）可以演变成线性律（Linear）和平方律（Square Law），具体的方程式如下式（2）和式（3）。20世纪90年代以来，随着科学技术的不断发展，先进的科技大量引入军队，极大地推动着军队形态由机械化向信息化的转变。随着军队信息化建设的深入发展，经典的兰切斯特方程组已经不适合用于像现代化战争这样高水平的对抗进行建模了。从公式上可以看出来经典兰切斯特方程组根本反映不出高科技对战争的影响。然而从近期伊拉克等多场战争中又可以看出这恰恰是最重要的，因此本文结合实际通过对经典的兰切斯特方程组进行改进，提出以前没有考虑到的影响战斗结果的因数，包括信息作战能力指数[4-5]以及战场暴露系数等多项因素，给出更加适合用于描述现代战争的兰切斯特战斗模型。希望对在进行这方面研究的学者提供一点参考方向。

式中，α＞0，β＞0表示非战斗减员系数，U(t)，V(t)表示作战双方的兵力补给。

式中，B，R分别表示双方的兵力，B≥0，R≥0，al、bl为红、蓝方战斗成员作战效能，as、bs分别为红、蓝方每个战斗成员在单位时间内平均毁伤对方战斗成员的数量。

1 兰切斯特战斗模型

1.1 建立战斗模型

兰切斯特线性律和平方律的建立都有基本的界定，线性律适用于双方均为区域射击，且为视线不良地区的作战，而平方律适用于双方均采用区域射击，且用于空旷地区的作战。由它们的界定可以看出线性律建立在双方相互“看得见”的情况下，而平方律则建立在双方相互“看不见”的情况下[6]。在现代化战争中，由于武器、装备等的不断更新，已经不能单纯用“看得见”和“看不见”来界定了。必须把两方面都考虑进去，具体体现在两个方面：（1）在时域上，当卫星扫描到的时候为“看得见”，而当敌军伪装到卫星侦察不到时或卫星扫描不到时为“看不见”。（2）在侦察能力上，战争的过程中总是不断地进行压制和反压制，被压制时，侦察能力很弱，主要表现为“看不见”，而反压制时，侦察能力强，主要表现为“看得见”。因此本文在线性律和平方律的基础上建立了新的现代化战争条件下的战斗模型，并引入红、蓝双方的信息作战能力系数εr、εb（战场使用信息的能力）和战场暴露系数Er、Eb(0≤Er≤1，0≤Eb≤1)对战斗模型进行修订，如下式（4）。这里Er=(1-fr)sb、Eb= (1-fb)sr（fr、fb为红、蓝方的伪装能力系数，sr、sb为红、蓝方的侦察能力）。

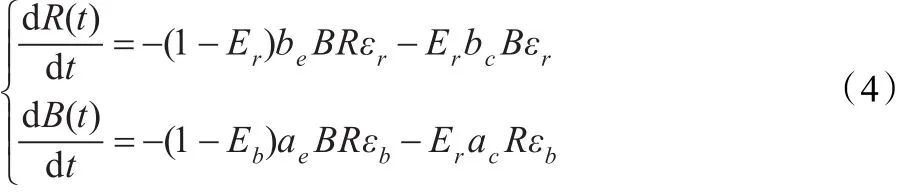
式（4）中，ac、bc表示红、蓝方平均每个士兵对暴露敌方士兵的杀伤率，称为暴露毁伤系数，ae、be是红、蓝方平均每个士兵对隐蔽敌方士兵的杀伤率，称为隐蔽毁伤系数。

由式（4）可得：

1.2 对兰切斯特战斗模型求解

由式（5）建立的新战斗模型可以看出它受到很多因素的影响，故也可以看出在现代战争中影响战争输赢的因素特别多，本文也只是提出了其中的几个。这里可以利用差分的方法来对战争双方的兵力情况进行求解，分别将线性律和平方律以及修订后的战斗模型写成差分方程的形式如下：

线性律方程[7-8]：

2 仿真实验和结果分析

2.1 影响因素仿真实验

需要比较的是不同暴露系数对战争的影响，故像毁伤系数这样对比较的结果影响不大的因素，这里设其为固定值。红方和蓝方的兵力以及毁伤系数相当，故这里可以设初始兵力R=5 000，B=5 000，al=bl=0.000 01，as=bs= 0.1，εr=4，εb=4。这里的伪装能力系数以及侦察能力系数如表1所示。

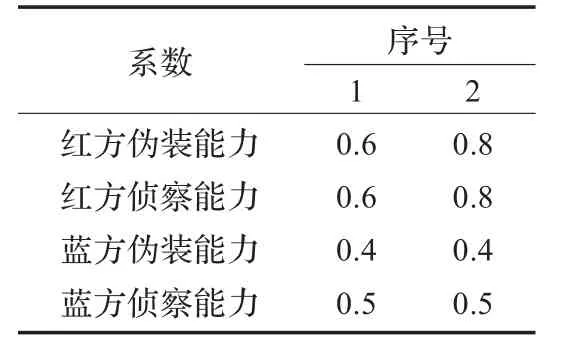
表1 能力系数变化情况

利用修订后的战斗模型对其进行计算得出的结果如图1，图2。

图1 在序号1数据下的结果

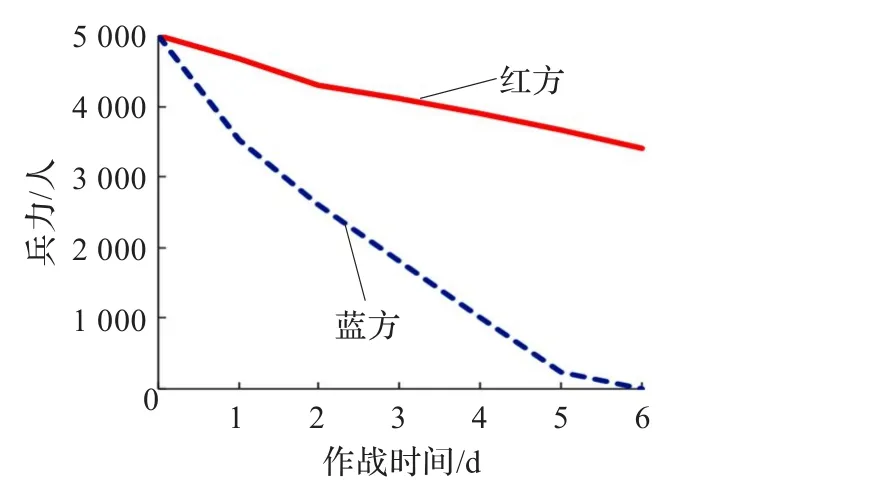
图2 在序号2数据下的结果

由图1可知，在现代战斗中就算兵力以及其毁伤系数都一样的情况下，结果也会出现很大的差距，在刚开始的时候就出现了兵力毁伤的差别，在8个单位时间以后红方就把蓝方给消灭了。由图2可知，随着两方使用的信息技术差距的拉大，其战斗时间就迅速下降，蓝方兵力毁伤率提高。只不到6个单位时间就被红方消灭了。通过两图的对比，可知在现代战争中科技对战争的进程影响是很大的。所以在对现代战争建立兰切斯特战斗模型的时候千万不能剔除科技因素对战争的影响。

2.2 修订后的战斗模型与经典模型仿真对比

假定红方的兵力以及毁伤系数都处于劣势，但其伪装能力、侦察能力以及对战场信息的利用能力都要强于蓝方，具体数据如下：R=8 000，B=10 000，al=0.000 02，bl=0.000 01，as=0.2，bs=0.1，εr=4，εb=4。

伪装能力系数以及侦察能力系数如表2所示。

利用平方律、线性律以及修订后的战斗模型对其进行计算得出的结果如图3～图5所示。

由图3和图4的结果可以看出，线性律或平方律模型的计算方式下，在没有考虑到科技信息技术的影响，红方都是输家，特别是在平方律模型下只有不到5个单位时间，红方兵力就全部被摧毁了。而蓝方的兵力毁伤不到2 000。这与近代的几场战争不符，像伊拉克战争、阿富汗战争等，并不是兵力越多它的胜算就越大的。在图5中把科技信息等因素考虑进去了，可以发现红方即使在兵力劣势的情况下，只要其有足够的信息作战能力以及侦察等方面的优势，也是可以取得胜利的。说明信息因素对现代战争的影响是非常大的。

通过仿真，发现修订后的兰切斯特战斗模型更加符合现代化战争的标准。本文通过对方程进行添加信息作战能力指数以及战斗暴露系数使其能反映出科技水平的差距，能建立出贴近实际的战斗模型，即现代化的兰切斯特战斗模型，为现代化战争的准备工作提供一些帮助。

图3 平方律结果

图4 线性律结果

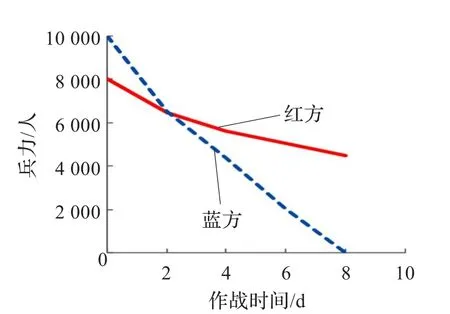
图5 修订战斗模型结果

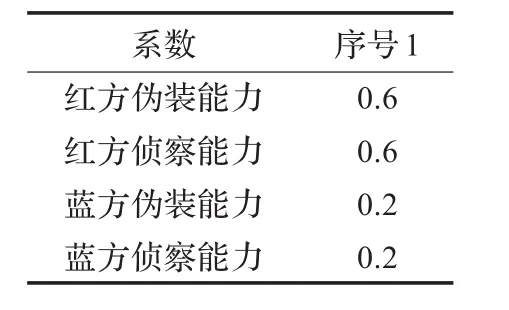
表2 能力系数对比

3 结论

当代社会已经是信息化、科技化社会，战斗的方式与以前有了很大的不同。特别是对于建立战斗模型的方式有了很大的变化，因此经典的兰切斯特方程已经不能完全地表达出其特征了。在这种情况下，本文提出了现代化战争条件下的兰切斯特战斗模型。该模型在保证老的毁伤系数的前提下，提出了新的影响因素并通过实验仿真得出它的可行性。因此该战斗模型对研究建立更适合现代战斗的兰切斯特方程战斗模型有很好的参考价值。

[1]MacKay N.Lanchester combat models[J].Mathematics Τoday，2006，42（5）：170-173.

[2]张啸天，李志猛，邓红艳.多维战争中兰切斯特方程探讨[J].火力与指挥控制，2008，33（2）：5-8.

[3]James G Τ.Lanchester-type models of warfare，AD-A090842[R]. 2000.

[4]王可定.作战模拟理论与方法[M].长沙：国防科技大学出版社，1999.

[5]郝海飞，王京鸣.炮兵弹药动态消耗规律[J].兵工学报，2011（3）.

[6]王京鸣，殷培江，齐建文.兰切斯特方程参数的一种计算模型[J].兵工学报，2005（1）.

[7]乔林峰，胡浩然，王俊.兰彻斯特方程的参数取值与计算[J].舰船电子工程，2011（8）.

[8]Yan Jinjiang，Wang Yong，Wang Xianyu.Modeling and simulation of Lanchester equation based on game theory[C]//Business Management and Electronic Information（BMEI），2011：212-214.

[9]Ingber L，Sworder D D.Statistical mechanics of combat with human factors[J].Math Compute Modeling，1991，15（2）：99-127.

ZHAN Donghui,CHEN Gang,ZHANG Hongjun,HAO Wenning,FENG Bo

Engineering Institute of Corps of Engineers,PLA University of Science&Τechnology,Nanjing 210007,China

In the modernized warfare,this paper presents Lanchester combat model for more suitable for modernized warfare through introducing information coefficient and combat exposure coefficient,amending damage factor in the classical Lanchester equation,based on analysing the classical Lanchester equation.

Lanchester-type equation;model;combat;modernized warfare;information

针对现代化战争，在分析经典兰切斯特方程的基础上，通过引入信息作战能力系数以及战斗暴露系数对经典兰切斯特方程进行修订，提出了更加适合现代化战争的兰切斯特战斗模型。

兰切斯特方程；模型；战斗；现代化战争；信息

A

ΤP391.9

10.3778/j.issn.1002-8331.1111-0358

ZHAN Donghui,CHEN Gang,ZHANG Hongjun,et al.Lanchester combat model in conditions of modernized warfare. Computer Engineering and Applications,2013,49（15）：246-248.

占栋辉，男，硕士研究生，主研方向：文本挖掘；陈刚，男，副教授；张宏军，男，博士，教授；郝文宁，男，博士，副教授；冯波，男，硕士研究生。E-mail：416275237@qq.com

2011-11-21

2012-02-13

1002-8331（2013）15-0246-03

CNKI出版日期：2012-05-09 http://www.cnki.net/kcms/detail/11.2127.ΤP.20120509.0845.004.html