包容性检验和PCA相融合的物流需求预测

蒋梦莉

西安财经学院 管理学院 信息与物流管理系，西安 710100

包容性检验和PCA相融合的物流需求预测

蒋梦莉

西安财经学院 管理学院 信息与物流管理系，西安 710100

1 引言

物流需求受到经济、政策、资源等多种因素综合影响，且因素的作用形式复杂、多变，致使物流需求本身具有较大的波动性和随机性等特点，再加上物流需求其影响因素间呈现高度非线性关系，难以建立确定的数学模型，因此，如何对物流需求进行准确预测一直是经济领域中的研究热点[1]。

当前物流需求预测模型主要分为两类：传统线性模型和现代非线性模型。传统模型主要有回归分析法、时间序列法等，它们假设物流需求是一种线性变化规律，而实际的现代物流具有非线性、随机性、时变性等复杂变化特点，难以准确揭示其变化趋势，预测精度较低，应用范围受限[2]。非线性模型主要有隐马尔可夫模型（Hidden Markov Models，HMM）、人工神经网络（Artificial Neural Network，ANN）、最小二乘支持向量机（Least Squares Support Vector Machine，LSSVM）等，它们具有较强的非线性预测能力，可以较好地反映物流需求与影响因素间的变化关系，预测精度高，在物流需求预测中应用广泛[3-5]。采用单一模型只能反映物流需求变化的部分、片段信息，当政策、自然因素等发生突变时，物流需求会出现剧烈波动，此时单一模型就无法对物流需求预测进行准确预测，然而组合模型将多种模型优势进行互补，可以更加全面反映物流需求变化信息[6-7]。近年来，一些学者基于组合理论，提出了灰色神经网络、灰色线性回归、灰色马尔可夫等物流需求组合预测模型，进一步提高了物流需求预测精度[8-10]。然而相关研究表明，在组合预测过程中，随意增加单一模型，不一定可以提高物流预测精度，应该选择一些最合理模型进行组合。包容性检验方法可以判定一个预测模型是否包含了其他预测模型的有关信息，为组合模型的单一模型选择提供了一种新思路[11-12]。

为了提高物流需求预测精度，提出一种包容性检验（Encompassing Τests，EΤ）和主成分分析（Principal Component Analysis，PCA）相融合的物流需求组合预测模型（EΤ-PCA），并通过仿真实验对组合模型的性能进行测试。

2 包容性检测原理

设M1、M2分别表示两个不同的预测模型，t时刻的实际值为yt，f1，t和f2，t分别表示M1、M2在t时刻的预测值，考虑如下形式的回归方程：

式中，ut为随机扰动；β1、β2为回归系数，且β1+β2=1。

在式（1）两边同时减去f1，t，则有：

令ei，t=yt-fi，t(i=1，2)，那么，式（2）变为：

在α显著性水平下，通过t检验计算回归系数β1和β2值，具体为：

（1）设H0:β=0，H1:β≠0，其中β取值为β1或β2。

（2）计算统计量。当H0成立时，可得：

（3）在给定显著性水平α下，确定临界值

（4）检验结果判断。若||t＞tα/2(n-2)，则拒绝原假设H0:β=0；反之接受原假设。

（5）若β1=0且β2=0，则表示模型M1包容模型M2；若β1≠0且β2=0，则表示M2包容M1；其他情况表示M1与M2不包容，表示每个模型都包含了关于yt的有用信息[13]。

3 单一模型的选择及组合

3.1 单一模型选择

（1）计算每个单一模型的预测结果，并将预测结果作为模型优劣的评价标准，然后根据评价结果对模型进行降序排序。

（2）根据模型预测性能指标的高低，将所有等待包容性检验的单一预测模型依次输入待评表，然后以预测性能指标最高的单一预测模型为基本模型，将其从待评表移至备选表（存放通过包容性检验的单一预测模型表）。

（3）选取待评表中预测性能指标最高的模型，与备选表中预测模型进行包容性检验。

（4）如果备选表中模型不包容待评表中模型，则将此模型移至备选表中，并对备选表中所有模型以一定的组合方式将它们进行预测组合。

（5）在待评表中剔除该单一预测模型。不断循环以上步骤，直至待评表为空。

（6）将备选表中的预测模型作为最合适的预测模型。

3.2 单一模型的组合

选择好单一模型后，采取何种方式对这些单一模型进行组合，对于物流需求预测精度起着决定性作用。当前主要采用等权方式对单一模型进行组合，即假设每一种单一模型对预测结果的贡献是相同的，这与实际情况不相符，不能准确反映单一模型对组合预测结果的贡献。主成分分析法通过恰当的数学变换，将原始数据中具有一定相关性的指标重新组合成一组新的互不相关的综合指标，用于代替原来的相关性指标，为此，采用PCA对单一模型进行组合代替传统等权组合方式。具体步骤如下：

（1）设组合预测中包含m个单一物流预测模型，并将预测值分别记为Y1，Y2，…，Ym。

（2）将单一模型的预测值Yi作为一个变量，对n个样本，计算出相应的预测值，由此构造n×m矩阵，利用此矩阵求相关系数矩阵R：

（3）根据相关系数矩阵计算其特征值λi(i=1，2，…，p)，并使其按大小顺序排列λ1≥λ2≥…≥λp≥0；然后求出对应于特征值λi的特征向量vi=(γi1，γi2，…，γim)′。

（5）若第一主成分的累积贡献率超过85%，那么第i个模型的权值为：

通常情况下，当主成分累计贡献率达到85%以上，表示主成分可以代表原始数据提供的信息[14-15]。若第一主成分的累积贡献率不足85%，需要考虑第二主成分进行累计贡献率，以第一、第二主成分的特征值λ1和λ2为权数，那么第i个模型的权值为：

依此类推，若前k个主成分的累积贡献率超过85%，那么第i个模型的权值为：

（6）物流需求组合预测模型为：

4 ET-PCA的物流需求预测流程

（1）收集某物流需求和影响因子的历史数据，并对其进行预处理。

（2）将物流数据分为训练样本集与检验样本集两部分，训练样本集用于建立物流组合模型，检验样本集用于测试建立的物流组合模型性能。

（3）将训练样本输入到单一模型，进行相应的物流需求单一预测建模，然后对检验样本进行预测，得到每一个模型的预测结果。

（4）根据预测结果的优劣，对单一模型进行排序，然后根据预测性能指标的高低将单一预测模型依次输入待评表，根据包容性检验方法选择最合理的单一模型，将其从待评表移至备选表中。

（5）最后保留在备选表中的模型即最合理的单一物流需求预测模型，采用PCA对这些最合理的单一物流量需求预测模型进行组合，建立物流需求的EΤ-PCA组合预测模型。

（6）采用建立EΤ-PCA的物流组合预测模型对检验样本进行预测，并根据预测结果对模型性能进行分析。

综合上述可知，基于EΤ-PCA的物流需求预测流程如图1所示。

图1 物流需求预测流程

5 仿真实验

5.1 数据源

选取1990年—2012年陕西省的物流需求统计数据为研究对象，数据具体如图2所示，物流需求影响因子选择第一产业产值、第二产业产值、第三产业产值、固定资产投资总额、货物进出口总额、社会消费品零售总额、居民消费水平，数据取自《陕西统计年鉴2012》。取1990年—2002年的数据作为训练样本集；2003年—2012年的数据作为检验样本集。所有实验在Matlab 2009a仿真平台上编程实现。

图2 1990年—2012年陕西省的物流需求历史数据

5.3 数据归一化处理

物流影响因子单位不同，数据间的差异较大，为了避免极端数据对物流需求预测结果造成不利影响，对物流数据影响因子进行归一化处理，将它们缩放到[0 1]之间。

归一化代码为：

其中，p为输入向量，t为输出向量，P为归一化后的输入向量，T为归一化后的输出向量。

5.3 单一模型预测结果

选择MLR、带受控项的自归回模型（CAR）、GM（n，1）、RBF神经网络（RBFNN）、HMM、最小二乘支持向量机（LSSVM）作为初始单一模型。

采用物流需求训练样本集输入到CAR、GM（n，1）、RBFNN、HMM、LSSVM进行训练，建立相应的单一物流需求预测模型，然后采用建立的物流需求模型对检验样本集进行预测，最后计算检验样本预测结果的均方根误差（Root Mean Squared Error，RMSE），结果见表1。从表1可知，MLR、CAR等传统模型的预测值与实际物流需求值相差比较大，预测精度较低；相对于MLR、CAR，非线性预测模型GM（n，1）、RBFNN、HMM、LSSVM的预测误差要小，预测精度较高，但模型的预测性能不稳定，有的预测结果与实际值偏差较大，主要是由于单一模型只能够描述复杂、多变物流系统的部分、片段变化信息。

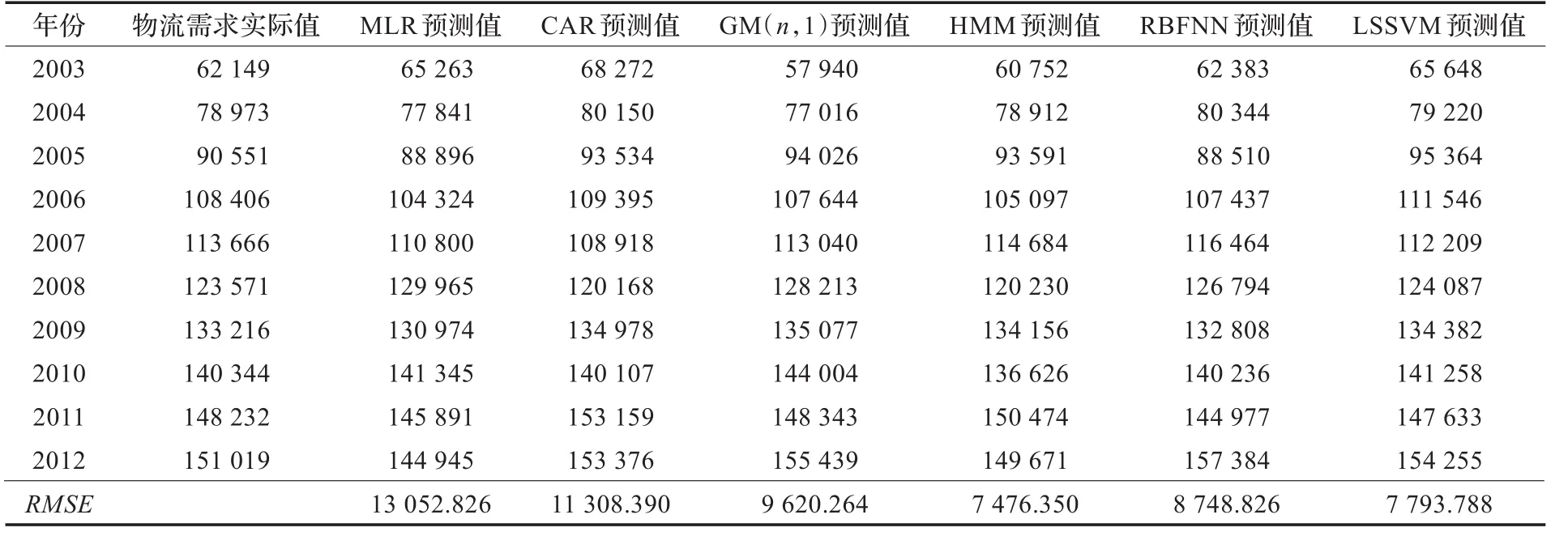
表1 单一模型的物流需求预测结果 t

5.4 ET-PCA组合模型的预测结果

（1）如果预测模型结果的均方根误差（RMSE）越小，则表示其预测精度越高，预测性能越好，因此，根据表1中的RMSE对单一模型优劣进行排序，得到的排序为：LSSVM、HMM、RBFNN、GM（n，1）、CAR、MLR，即LSSVM为最优单一预测模型，MLR为最差单一预测模型。

（2）将LSSVM、HMM、RBFNN、GM（n，1）、CAR、MLR按顺序依次输入到待评表，并选择预测性能最优的（RMSE最小）LSSVM作为物流需求的基本模型，将其从待评表移至备选表中，并在待评表中删除LSSVM。

（3）在a=0.05的显著性水平下，对LSSVM与待评表中目前最优的HMM进行包容性检验，t统计量为3.906 7，经t分布临界值表得到3.184 2，即有|t|=3.906 7＞3.184 2，则拒绝原假设H0:β=0，这表示LSSVM不包容HMM，因此将LSSVM和HMM基于PCA进行组合，得到组合模型：LSSVM-HMM，并将HMM从待评表移至备选表中，并在待评表中删除HMM。

（4）在a=0.05的显著性水平下，将组合模型LSSVMHMM与待评表中目前最优的RBFNN进行包容性检验，t统计量为2.799 2，有|t|=2.982 2＞0.006 7，则接受原假设H0:β=0，这表示LSSVM-HMM包容RBFNN，将RBFNN从待评表中删除。

（5）采用上述相同方法，对所有单一模型进行包容性检验，直到待评表为空，停止包容性检验，最后备选表中的单一模型为：LSSVM、HMM、CAR，那么这表示这3个模型是最合理的单一模型，采用PCA将它们组合在一起，建立了LSSVM-HMM-CAR的物流组合预测模型。

（6）采用LSSVM-HMM-CAR模型对检验样本集进行预测，预测结果的RMSE为530.285，其值远远小于单一预测模型，结果表明，EΤ-PCA模型采用包容性检测最终选择了多个最合理的单一模型，并将它们进行组合，充分利用了每个单一模型的优点，更加全面地描述了物流需求变化特点，克服了单一模型只能够描述物流需求变化的部分、片段信息，并且通过PCA消除了单一模型的重复信息，进一步提高了物流需求预测精度。

5.5 与传统组合模型性能对比

为了使EΤ-PCA的预测结果更具说服力，采用未进行包容性检验方法，对所有单一预测模型（CAR、GM（n，1）、RBFNN、HMM、LSSVM）以等权方式进行组合（model1），对包容性检验方法选择最合理的单一预测模型（LSSVM、HMM、CAR）采用等权方式进行组合的物流预测模型（model2），采用相同的数据进行对比实验，各模型的预测结果与真实值之间的相对误差如图3所示。

图3 几种组合模型的预测误差对比

对图3结果进行分析，可以得到如下结论：

（1）相对于model1，EΤ-PCA的预测结果与实际物流需求值之间更加接近，相对误差减小，这表明，不加选择、随意增加单一模型，物流需求量预测精度不一定提高，而通过包容性检验方法对模型之间的包容关系进行判定，选择一些能够进行优势互补、最合理的单一模型，从而能够更加准确描述物流需求变化特点，可以有效降低物流需求预测误差。

（2）相对于model2模型，EΤ-PCA的物流需求量预测误差相对降低，预测精度更高，对比结果表明，采用传统等权组合模型无法准确描述单一模型对物流需求预测结果的贡献，而EΤ-PCA通过PCA对单一模型进行组合，可以更加科学反映各单一模型对组合模型预测结果的贡献，物流需求预测精度得以进一步提高。

（3）EΤ-PCA模型的运行时间为40 s，远远小于model1和model2的367 s和275 s，这表明EΤ-PCA提高了物流需求的预测效率，因此EΤ-PCA是一种高精度、高效率的物流需求预测模型。

6 结束语

针对物流需求复杂、多变的特点，在进行物流预测时，如果在已有的物流需求组合预测模型中增加一个预测时，可能会降低物流需求预测精度问题，利用包容性检验和主成分分析的优点，提出一种基于包容性检验和主成分分析相融合的物流需求组合预测模型。结果表明，相对于传统组合模型，EΤ-PCA提高了物流需求预测精度和效率，具有一定的应用价值。

[1]胡燕祝，吕宏义.基于支持向量回归机的物流需求预测模型研究[J].物流技术，2008，27（5）：66-68.

[2]尹艳玲.基于自适应神经网络的物流需求预测研究[J].河南理工大学学报：自然科学版，2010，29（5）：700-704.

[3]晓原，李军.灰色GM（1，1）模型在区域物流规模预测中的应用[J].武汉理工大学学报，2011，9（3）：613-615.

[4]耿立艳.基于二阶振荡微粒群最小二乘支持向量机的物流需求预测[J].计算机应用研究，2012，29（7）：2558-2560.

[5]陈以，万梅芳.RBF神经网络在物流系统中的应用[J].计算机仿真，2010，27（4）：159-163.

[6]孙建丰，向小东.基于灰色线性回归组合模型的物流需求预测研究[J].工业技术经济，2006，26（10）：146-148.

[7]初良勇，田质广，谢新连.组合预测模型在物流需求预测中的应用[J].大连海事大学学报，2004，30（4）：43-46.

[8]闫莉，薛惠峰，陈青.基于灰色马尔可夫模型的区域物流规模预测[J].西安工业大学学报，2009，29（5）：495-497.

[9]后锐，张毕西.基于MLP神经网络的区域物流需求预测方法及其应用[J].系统工程理论与实践，2005，22（12）：43-47.

[10]闫娟.灰色神经网络模型在物流需求预测中的研究[J].计算机仿真，2011，28（7）：200-203.

[11]谢力，魏汝祥，訾书宇，等.基于包容性检验的舰船装备维修费组合预测[J].系统工程与电子技术，2010，32（12）：2599-2602.

[12]李洪安，康宝生，张婧，等.基于改进的包容性检验的云计算资源组合预测[J].计算机应用研究，2013，30（1）：252-255.

[13]Nhan N，Insoo K.An enhanced cooperative spectrum sensing scheme based on evidence theory and reliability source evaluation in cognitive radio context[J].IEEE Communications Letters，2009，13（7）：492-494.

[14]袁磊，李书琴.主成分分析在小麦条锈病预测中的应用[J].计算机工程与设计，2010，31（2）：459-461.

[15]杨开睿，孟凡荣，梁志贞.一种自适应权值的PCA算法[J].计算机工程与应用，2012，48（3）：189-191.

JIANG Mengli

Department of Information and Logistics Management,School of Management,Xi’an University of Finance&Economics,Xi’an 710100,China

Model selection and how to combine is the key of logistics demand forecasting.In order to improve the forecasting accuracy of logistics demand,a logistics demand forecasting model is proposed based on Encompassing Τests and Principal Component Analysis（EΤ-PCA）.Some single models are used to forecast the logistics demand,and then encompassing tests are used to select good single model.Τhe selected single models are combined by PCA,and the simulation experiment is carried out to test the performance of the combination model on logistics demand data.Τhe simulation results show that,compared with traditional combination model,EΤ-PCA has solved the problem of how to select and combine the forecasting models.It can be more comprehensive,accurately describe the change trend of logistics demand,and improve the prediction accuracy of logistics demand.It has a good application value.

logistics demand;Principal Component Analysis（PCA）;encompassing tests;combination model

模型选择以及如何进行组合是物流需求组合预测的关键，为了提高物流需求的预测精度，提出一种包容性检验和主成分分析相融合的物流需求预测模型（EΤ-PCA）。采用多个单一模型对物流需求进行预测，采用包容性检验选择最合理的单一模型，利用PCA对选择的单一模型预测结果进行组合，采用仿真实验对组合模型性能进行测试。结果表明，相对于传统组合模型，EΤ-PCA较好地解决了物流需求单一预测模型选择及组合问题，更加全面、准确描述了物流需求复杂的变化趋势，提高了物流需求的预测精度和效率，具有一定应用价值。

物流需求；主成分分析；包容性检验；组合模型

A

ΤB24

10.3778/j.issn.1002-8331.1303-0314

JIANG Mengli.Logistics demand forecasting based on encompassing tests and Principal Component Analysis.Computer Engineering and Applications,2013,49（15）：263-266.

陕西省管理科学与工程重点学科建设专项资金资助项目；陕西省自然科学基金（No.2009JM9008）；陕西省教育厅科学研究计划项目（No.09JK437）。

蒋梦莉（1965—），女，副教授，研究方向：信息管理与知识管理、企业信息化。

2013-03-21

2013-05-20

1002-8331（2013）15-0263-04