圆锥曲线形成和发展的历史过程及其教学启示

陆源

（集宁师范学院数学系，内蒙古乌兰察布012000）

圆锥曲线形成和发展的历史过程及其教学启示

陆源

（集宁师范学院数学系，内蒙古乌兰察布012000）

圆锥曲线是中学数学的重要内容从数学史的角度看，圆锥曲线是在经历古希腊的古典时期、亚历山大前期、亚历山大后期到16世纪以后的整个历史时期而不断形成、发展和完善起来的.在教育形态上，它是经过编者的精心选择和编排，最终体现为一个完美的演绎系统.圆锥曲线的形成和发展历史过程对数学教学有重要启示.

圆锥曲线；形成；发展；数学教学；启示

1 圆锥曲线形成和发展的历史过程

圆锥曲线是中学数学的重要内容，在教材中包括抛物线、椭圆、双曲线的共性，如：中心、对称性、焦点、离心率、准线、渐近线、标准方程等和它们分别独具的特点.从数学史的角度看，圆锥曲线是在经历古希腊的古典时期、亚历山大前期、亚历山大后期到16世纪以后的整个历史时期而不断形成、发展和完善起来的.在教育形态上，经过编者的精心选择和编排，最终体现为一个完美的演绎系统.

1.1 门奈赫莫斯首次发现圆锥曲线

公元前4世纪，古希腊古典时期柏拉图学派的门奈赫莫斯（Menaechmus）首先发现了圆锥曲线，他用平面去截圆锥曲面而得到的截痕.在当时，圆锥曲面的形成是通过以直角三角形的一条直角边为轴旋转而成的，根据轴三角形顶角的不同将圆锥曲面分为锐角圆锥、钝角圆锥和直角圆锥. Menaechmus用垂直于一条母线的平面去截这三种圆锥面，得到三种不同的截痕.在锐角圆锥上的截痕是椭圆，钝角圆锥上的截痕是双曲线（一支），直角圆锥上的截痕是抛物线.

如下图1，直角圆锥面ABC，过其母线AC上的任意一点D作垂直于AC的一个平面，得截平面DPGE.过截线上的点P作一平行于圆锥底面的平面交母线于R、V两点，则RV是截面圆的直径,RV交PQ于O,连接PQ.

图1

由平面DEG⊥平面ABC，平面PVR⊥平面ABC

∴PQ⊥平面ABC∴PQ⊥RV

∵RV是圆的直径∴根据射影定理有PO2=RO·OV①

结合①②,得PO2=RO·，由于对于特定的D点是常量，所以不妨设令OP=y，DO=x,那么有y2=bx.

用现代解析几何解释为：曲线上任一点的纵坐标的平方等于其横坐标乘以一个常数，即为抛物线.同理，如果顶角是钝角或锐角，可以推出另外两种圆锥曲线的性质.

1.2 阿波罗尼奥斯对圆锥曲线的研究

后来又有许多数学家研究这一课题.古希腊亚历山大前期的著名数学家阿波罗尼奥斯(Appolonius,公元前262年—前190年）完成了他的《圆锥曲线论》（8大卷）经典巨著.他首创了只用一个圆锥面，就可以截得三种圆锥曲线，首先他改变了产生圆锥面的办法：给定一个圆及圆所在平面外一点V，联结V与圆周上的点并向两端延长.令这条直线沿着圆周移动，最后回到出发点，就形成圆锥曲面的两部分.固定点V叫做顶点，定圆叫做底面，点V与圆心的连成叫做轴.轴垂直于底面的圆锥是正圆锥，不垂直的是斜圆锥.

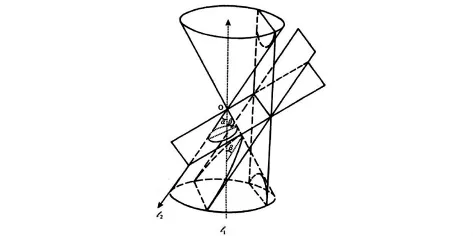
图2

当时，Appolonius还不知道坐标系，他首先通过平面去截圆锥的一腔形成椭圆，用类似于坐标系的方法求出来的椭圆方程在现代椭圆标准方程中，若将坐标原点（0，0）移到（-a，0），则新坐标系下的方程只需将x=x'+a,y'=y替换，即得这就与阿波罗尼奥斯求出来的方程形式一样了.

他通过改变平面去截圆锥面的角度，可得到另外两种截线.若截平面与底圆相交，而且和圆锥面的另一支也相交，便得到双曲线，其方程为若截平面平行于一条母线，则与底圆相交，但只与圆锥的一支相交，这时得到抛物线方程为y2=px

当时阿波罗尼奥斯已借助坐标来描述圆锥曲线，对圆锥曲线的全部性质的研究达到了非解析几何意义下综合演绎几何学的最高峰.这三种圆锥曲线的命名源于阿波罗尼奥斯，分别叫做椭圆、双曲线、抛物线.他用统一的方式得到了三种圆锥曲线，既总结前人的工作，又进一步自己研究了许多性质.如中心、切线、焦点等，形成了完美的圆锥曲线论.

1.3 帕波斯对圆锥曲线的研究

公元4世纪，亚历山大后期的著名数学家帕波斯（Pappus，公元300年—公元350年）在其名著《数学汇编》中研究了圆锥曲线及其性质.

1.3.1 用不通过圆锥顶点V的平面去截一个直圆锥.把两个球面别放在截面的上方和下方，和截相切于F1与F2两点，这两球面又与圆锥面相切于两个圆.在椭圆上任取一点M，过M引线段AB，A、B分别为两球与圆锥面的切点.则由直线MA、MF与球面相切，有MA=MF1，直线MB、MF2与另一个球面相切，有MB=MF2，于是，MF1+MF2=MA+MB=AB=常数，因此得出结论：椭圆是截面上所有点M的集合，M与截上两个定点F1、F2距离之和是一个常数，点F1、F2称为椭圆的焦点.

1.3.2 若截面与圆锥的两腔相交，即平行于圆锥面的两条母线确定的平面，则得到的截线是双曲线，两个球分别放入圆锥的两腔中，使它们分别与截面相切于点F1，F2，且它们分别与圆锥面切于两个圆.在双曲线上任取一点M.同理可得MF1=MA，MF2=MB，其中，M、B、V、A在一条母线上，V是顶点，于是，MF1-MF2=MA-MB=AB=常数.而AB的长是一定的，与M点的选取无关；故|MF1-MF2|=常数.

于是得出结论：双曲线是点M的集合，它的每个点与这平面上的两点的距离之差的绝对值是一个常数.（若M取在另一支上，则MF1-MF2是负的，但绝对值不变.）点F1、F2称为双曲线的焦点.

1.3.3 若截面与圆锥的一条母线平行，与圆锥面的一腔相交，截得的曲线称为抛物线.

作一球面使它与圆锥相切于一个圆周与截面相切于点F，在抛物线上任取一点M，则MF=MA

（A为圆锥面与球的切点）.球与圆锥面相切的圆所在的平面与截平面相交于一条直线.得出结论：

抛物线是动点M的集合，M与这平面上一个定点F及一定直线距离相等.点F叫做抛物线的焦点，定直线叫做准线.

椭圆与双曲线也有准线且各有两条准线，这些准线是截面与两球面和圆锥相切的圆所在平面的交线.通过焦点与准线可以得出三种圆锥曲线统一定义：

点M到定点F与到定直线的距离之比是一个非零常数e，e＜1的是椭圆，e=1的是抛物线，e＞1的是双曲线.点F与准线在截面上，F不在准线上.这就是帕波斯通过焦点与准线的观点给出的圆锥曲线的标准定义.

1.4 16世纪以后圆锥曲线的发展

16世纪科学史上，与圆锥曲线有关的两项工作是：（1）开普勒发现行星按椭圆形轨道运行；（2）伽俐略证明了不计阻力的斜抛运动轨迹是抛物线.这就说明了圆锥曲线并不是依附于圆锥之上的“静态曲线”，而是有在于自然界的物体常见的运动形式，为运用运动的观点来研究圆锥曲线问题做了重要准备.

1629年，法国数学家费尔马引用斜角坐标研究圆锥曲线，得出的结论：圆锥曲线的方程都是含有两个未知数且最高次数为二次的方程.

1637年笛卡儿创立解析几何，其中的坐标法、平面上的点和实数（x,y）一一对应，“静”的曲线是点运动的轨迹、代数方程可表示曲线等思想，铺设了通往现代圆锥曲线理论的金光大道.英国数学家沃利斯在《圆锥曲线论》一文中，用关于x,y的二次方程来表示圆锥曲线，把圆锥曲线从圆锥面的截线中解脱出来，成为一种平面曲线.1748年，欧拉在《无穷小分析引论》一书中详细讨论了形如Ax2+Bxy+CY2+DX+ EY+F=0的一般二次方程，证明可以通过坐标的平移和转轴两种变换，把任何一个二次方程化为9个标准型（椭圆型、双曲线型、抛物线型）中的一个（包括退化的圆锥曲线，如圆等），这就是我们现在教材中出现的标准方程.

2 教学启示

从上述圆锥曲线的形成和发展过程中，我们可以看到它是经过几代数学家的坚持不懈地探索，逐渐把古希腊学者对圆锥曲线深奥难懂的文字表达变为通过坐标系和标准方程这样简洁、清晰的表示.

2.1 现行教科书中的圆锥曲线理论知识是经过了2000多年来一代代数学家孜孜不倦追求真理的结果，多么地来之不易呀！整个发展过程中蕴含的丰富思想和方法对我们现代中学数学教学有着重要的借鉴作用.数学家的执著追求的精神对中学生来讲也具有重要的教育意义.

2.2 数学教师不能只是一味地追求数学理论的严密性、系统性，而需收集整理数学史料，不能仅局限于教材内容，而需重新审视、挖掘这些内容背后的历史，弄清知识的来龙去脉，然后采取适当的方式融入到教学中.了解圆锥曲线统一定义的由来有助于提高中学生的理解水平，使学生不会感到突如其来、深奥难懂.

〔1〕梁宗巨.世界数学通史[M].沈阳：辽宁教育出版社，2001.

〔2〕梁宗巨.数学历史典故[M].沈阳：辽宁教育出版社，2000.

〔3〕王树禾.数学思想史[M].北京：国防工业出版社，2003.

O174

A

1673-260X（2013）06-0017-02