比较政治分析中的模糊集方法

何俊志

在社会科学研究中，如果要划分以量化思维为基础的数学模型，大致可以在两个层次上展开。在第一个层次上，可以根据量化推理是否具有确定性而区分为确定性模型和不确定性模型。在确定型模型中，对象之间的关系具有必然性，所采用的方法主要是经典数学的方法，例如微分方程和差分方程等。在第二个层次上，不确定性模型又可细分为以随机数学为基础的随机模型和以模糊数学为基础的模糊数学模型。在前一模型中，对象之间的关系具有偶然性;在后一种模型中，对象之间的关系具有模糊性。

随着行为主义的兴起和理性选择理论的发展，以随机数学为基础的统计推理和以确定性数学为基础的理性选择理论及博弈论，长期以来一直居于政治学研究方法的主流地位。前者以其大数量处理的优势见长，而后者则因其模型的精致和简约而吸引着越来越多的研究者。

但是，对于那些案例数量不是太多从而达不到统计要求，需要经验因果推理而又无法演绎的问题，如果仍然采用传统的形式逻辑的方法进行因果推导，则既难以解决多重因果关系的推理，又无法提出精致的解释，因而长期被认为是一个研究方法相对滞后的领域。所幸的是，以模糊数学为基础的模糊集方法和技术在社会科学研究中的扩展，为这一领域的研究带来了新的生机。

一、比较方法从密尔法到布尔法的发展

在社会科学的小数量案例研究中，密尔在《逻辑体系》一书中所倡导的寻求因果关系的逻辑方法，曾经被托克维尔、马克·布洛克、巴林顿·摩尔和西达·斯考切波等经典的社会科学家用来解释一些历史上所发生的重大事件，并产生过广泛的影响①［美］西达·斯考切波:《国家与社会革命》，何俊志、王学东译，上海人民出版社2007年版，第37页。。密尔五法，即求同法、求异法、求同求异并用法、剩余法和共变法，作为一套归纳推理的逻辑方法，在相当长的时间内都是一些学者试图超越简单枚举推理而采用的基本方法。

密尔五法中，由于剩余法只考察一个案例，因而不适用于比较分析。在其余的四种方法中，前三种方法在本质上都是一种排除法，即通过排除给定现象的某个或某些可能的原因以支持某一因果解释。在事物之间出现程度上的变化时，原有的排除法就不可行，因而共变法就成了一种归纳推理中的定量方法，从而也就是一种统计方法。

基于前三种比较方法与共变法的这种差异，在比较学者们内部就出现了两种不同的观点。一种观点认为，以共变法为基础的统计方法与前三种方法之间存在着明确的区分。例如，马克斯·韦伯就认为，实验法、统计法和比较法是三种不同的方法;涂尔干则认为，当实验法不可行时，就只有共变法可用，求同法和求异法由于不能控制另外的变量，因而是不可用的②［加］约翰·福克斯:《社会科学中的数理基础及应用》，吴晓刚主编，格致/上海人民出版社2011年版，第269页。。另一种观点则认为，尽管这两类方法存在着一些具体的差异，但就其本质而言，都是一种比较的方法。例如，阿尔蒙德就认为，没有必要在政治学中强调比较的方法，因为科学方法在本质上就是比较的。在这个意义上，甚至说在政治科学中存在一个比较政治学分支都是没有意义的③Gabirel A.Almond，Political Theory and Political Science，The American Political Science Review，Vol.60，No.4(Dec.，1966)，pp.869-879.。李帕特则认为，在比较方法与实验方法和案例研究之间存在着明晰的边界，但比较方法和统计方法之间则没有明确的界线④Arend Lijphart，The Comparable-Cases Strategy in Comparative Research，Comparative Political Studies，Vol.8，No.2(July 1975)，pp.158-177.。还有一些比较学家甚至认为，可以用同一种推理逻辑，将比较政治分析区分为比较单个国家、比较一些国家和比较许多国家这样三个数量上的层次⑤Todd Landman，Issues and Methods in Comparative Politics(Third Edition)，Abingdon:Routledge，2008，pp.24-28.。所谓的比较法和统计法的差异，在他们看来就只存在数量上的区别。

不过，无论赞同共变法与上述三法之间是否存在着差异，更多的研究者在操作层面上还是倾向于将小样本的比较与大样本的比较进行一定的区分。在将大样本的比较明确为统计法之后，狭义的比较法就主要是指小样本的比较。在对小样本进行比较的求同法、求异法和求同求异并用法中，后者又只不过是对前两种方法的间接运用，因此主要的方法就只剩下求同法和求异法。

但是，无论是密尔的求同法还是求异法，其共同存在的一个问题在于，它们都只能识别出现象发生的一个原因。这就是一种无法控制其他变量因而难以排除其他原因的方法。当某一现象的发生很可能与多个因素有关时，无论是求同法还是求异法，都无法识别出影响某一现象发生的多种原因。所幸的是，布尔代数及其逻辑真值表的引入，就可以在密尔法的求同法和求异法的基础上识别出多种原因，从而将密尔法改造为布尔法。布尔法的基本思路是:将事物出现/不出现表示为1/0这样一种二分变量 (定距变量则可以区分为一系列的二分变量)。以二分法为基础，利用集合论的基本原则，就可以建立起一套逻辑真值表⑥［美］S.利普舒尔茨、M.利普森:《离散数学》，周兴和、孙志人、张兴斌译，科学出版社2002年版，第374页。。这一真值表既可以反映出事物发生或不发生的多种条件，同时还可以从中看出，多种条件出现或不出现之间的组合关系，是如何在导致某一现象发生或不发生。简言之，在布尔法的真值表中，既可以看到某一结果出现的多个必要条件，也可以看出某一结果发生的充分条件。

在表1中，假设我们收集到了五个案例，并且收集到了与结果发生有关的三个可能性条件，其中有三个案例发生了某种结果。首先我们发现，在案例1中，条件1、条件2和条件3共同出现，是结果出现的充分条件;在案例2中，条件1就构成了结果出现的充分条件;在案例3中，条件1和条件3构成了结果出现的充分条件。而凡是在结果发生的案例中，条件1都有出现;凡是在结果没有发生的案例中，条件1都没有出现。因此，我们可以得出结论认为，条件1是结果发生的必要条件。

表1 布尔法的简要逻辑真值表

但是，在我们得出条件1是结果发生的必要条件的同时，却并不能有效解释在结果出现的三个案例中，各种条件是如何组合在一起，共同导致某种结果出现的。布尔法的真正要义在于，它还能够揭示出这些条件之间的具体组合方式及其与结果的关系。

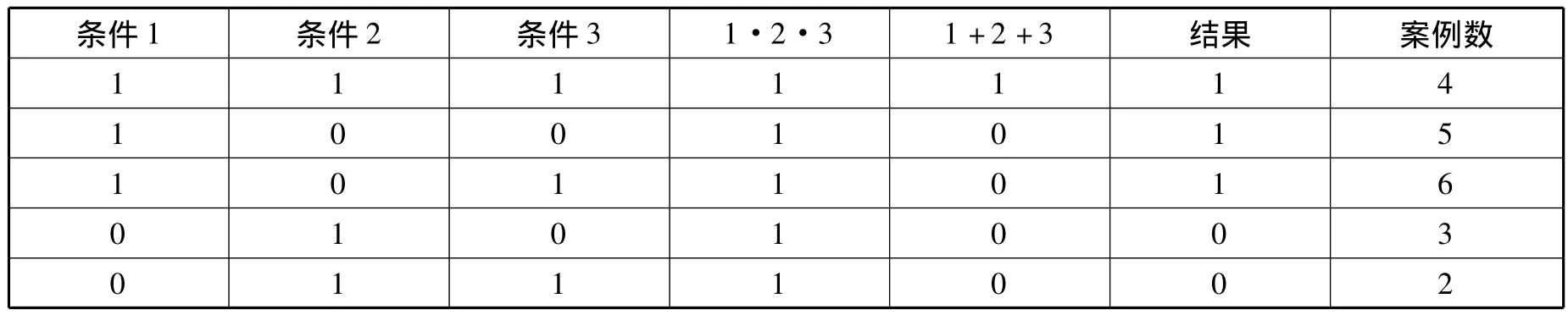
表2 布尔法的真值计算表

在布尔代数中，乘法为交集，表示“和”;加法为并集，表示“或”。依据表2，我们可以分离出多种因果关系:在表2所示的4个案例中，(条件1·条件2·条件3)+(条件1+条件2+条件3)，构成了结果发生的充分条件;在5个案例中，(条件1)· (－条件2)· (－条件3)+(条件1)+(－条件2)+(－条件3)，构成了结果发生的充分条件;在6个案例中，(条件1)· (－条件2)· (条件3)+(条件1)+(－条件2)+(条件3)，构成了结果发生的充分条件。

在运用布尔法进行计算时，还需要采用一种“最小化”(minimization)原则。这一原则要求在进行数值运算时，要尽量去除那些不必要的条件。表2为我们提供的三组因果机制中，在考察三个条件的交集与并集导致与结果的关系时，只有三个条件的交集才构成结果发生的必要条件。再考察条件1、条件2与条件3的交集时，无论条件2与条件3是否出现，结果都会发生，因此我们在求三者的交集时，完全可以把条件2和条件3去除，只保留条件1作为结果发生的必要条件。我们的最后结论是，在表2的三种因果机制中，只有条件1才是结果发生的必要条件①Charles C.Ragin，The Comparative Method，Moving Beyond Qualitative and Quantitative Strategies，Berkeley:University of California Press，1987，pp.93-94.。

值得注意的是，由于这里一共三个条件，三个条件之间从理论上应有2×2×2=8种可能的组合。但我们只收集到了五组案例，这五组案例并没能够穷尽三个条件之间的所有可能组合。布尔法的优点正在于，剩下的三个在理论上可能、在现实中没找到的案例，正是我们要构造的反事实推理 (counterfact inference)机制和理论预测的基本模式。由于我们在理论上已经穷尽了三个条件的所有可能性，每一类案例在数量上的增加，就只有可能丰富而不是削弱我们的推理②Charles C.Ragin，Fuzzy-Set Social Science，Chicago，The University of Chicago Press，2000，p.127-128.。而与统计推理不同的是，某一类型的具体案例数的多少，对这里的逻辑推理来说并不重要。

通过查尔斯·拉金和克里斯·德拉斯 (Kriss Drass)的共同努力，以布尔法为基础的逻辑真值表的分析方法，被发展成为一种以计算机软件为辅助的清晰集定性比较分析方法 (csQCA，Crisp-Set Qualitative Comparative Analysis)。在拉金看来，在整个社会科学的发展史上，涂尔干所倡导的方法，主要是一种变量导向的方法;韦伯所倡导的方法，则是一种案例导向的方法①Charles C.Ragin，David Zaret，Theory and Method in Comparative Research:Two Strategies，Social Forces，Vol.61，No.3(Mar.，1983)，pp.731-754.。而以布尔法为基础的清晰集方法，体现的正是一种案例导向的比较方法。

二、集合论从清晰集到模糊集的深化

清晰集方法虽然已经在很大程度上超越了传统比较方法的一些缺陷，将传统的定性方法推向了较为精致化的程度;但它的适用范围仍然非常有限，因为它只能处理条件变量和结果变量均为二分变量的案例。对于统计分析中所大量采用的定距变量，清晰集方法只能望而却步。所幸的是，模糊集合理论的引入，就在很大程度上突破了清晰集方法的这一瓶颈。

简而言之，模糊集合理论认为，传统集合论的最大缺陷在于，认为集合之间的关系存在着明确的界限，而现实之中的集合间关系并不完全如此。通过引入隶属度 (degree of membership)这一概念，模糊集合理论就将集合之间的关系处理为一种程度关系。当集合A完全包含于集合B时，集合A就完全隶属于集合B，其隶属度为1;当集合A与集合B没有交集时，集合A隶属于集合B的程度就为0;当集合A与集合B之间相交时，根据相交的程度，集合A隶属于集合B的情况就分为0至1之间的不同数值。由此，在将A作为条件变量而将B作为结果变量时，A是否会导致B发生的问题，就转换成了A在多大程度上出现，会在多大程度上导致B的发生。自控制论学者扎德 (L.A.Zadeh)于1965年在《信息与控制》杂志上发表“模糊集合”一文以后，模糊集合理论已经在自然科学和社会科学中得到了广泛的应用②原文参见:Zedah，L.，Fuzzy Set.Information and Control，Vol.8，1965，pp.338-353.模糊集合的应用可参见 Hans-Jürgen Zimmermann，Fuzzy Set Theory and Its Applications(forth edition)，Dordrecht(The Netherlands):Kluwer Academic Publishers Group，2001。。

根据这一基本原理，清晰集意义上的集合A与集合B之间的关系，就被转化成了A与B之间的隶属度是0还是1的关系。在0与1之间，则可以将定距变量处理成隶属度分数。例如，A为某个政党所投入的竞选经费，B为某个政党所获得的选票数。此时，我们需要做的工作，仅仅是将各个政党所投入的经费与该党所获得的选票总数，转化为0到1之间的隶属度分数即可。

在将集合之间的关系处理成0到1之间的隶属度关系后，对集合与进行的交集和并集的运算仍然等同于传统的集合论。例如，A的隶属度分数为0.8，B的隶属度分数为0.3，则A与B的交集为0.3，A与B的并集为0.8。与传统集合论的差异在于，在传统集合论中，某一集合与其补集的交集为空集;但在模糊集合中，某一集合与其补集的交集是取最小值。例如，A的隶属度为0.8，其补集为0.2，A与非A的交集就为0.2而不是空。也就是说，在模糊集合的运算中，排中律不成立。不过这正符合模糊集合的基本原理，即是与非之间有时并无明确界限。

模糊集分析的第二个原理，部分类似于统计分析中将原始数据转化为标准化分数 (Z分数)的过程。这个被称为是“校准”(calibration)的过程，就是将原始数据转化成隶属度分数的过程。显然，如果隶属度分数为1，就表示完全隶属关系;隶属度分数为0，就表示完全没有隶属关系;隶属度分数为0.5，就表示半隶属关系③Charles C.Ragin，Fuzzy-Set Social Science ，Chicago，The University of Chicago Press，2000，pp.155-160.。例如，通过观察，我们发现，在参加选举的5个政党中，甲、乙、丙、丁、戊五个政党所投入的经费分别为3000万、2700万、2100万、1400万、800万;所获得的选票分别为90万、72万、53万、40万、12万。如果我们将投入经费低于1200万视为低隶属关系，投入经费为2000万视为中隶属关系，投入经费为2800万为高隶属关系，那么，就可以依据上述三个分界点，将五个政党投入经费的隶属度计算出来;同理，也可以将其所获选票的隶属度计算出来。

一旦将各个变量的原始数值转化成［0，1］之间的隶属度分数之后，模糊集理论就主要考察各个变量及其案例之间的隶属度关系。其中最主要的关系，就是各条件变量与结果之间的隶属关系。与统计方法的另一个类似之处是，当我们在布尔真值表中将各种有可能影响结果的条件及其隶属度分数分列出来之后，各个条件之间的关系是并集关系。即每个条件出现导致结果发生的可能性。如果有理论或证据表明，某两个或两个以上的条件共同出现之时才能导致结果的发生，在统计方法中是建立一个将两个变量相乘而得出的交互变量，并观察交互变量是否会对因变量产生显著影响。布尔法在这里所采用的方法是，将那些有可能共同影响结果的变量处理成交集。而模糊集方法则是将二者求交集时取隶属度分数的最小值。

通过将各个条件变量和结果变量都转化为隶属度分数后，接下来要回答的一个基本问题是:这些变量之间是否在集合论意义上存在着某种关系?如果存在着某种关系，我们就可以肯定，各条件变量的组合，是导致结果变量出现的原因。拉金认为，通过一致性 (consistency)和覆盖度(coverage)的计算，就可以确证这一关系是否存在。所谓一致性，是指纳入分析的所有案例在多大程度上共享了导致结果发生的某个给定的条件或条件组合;所谓覆盖度，是指这些给定的条件或条件组合，在多大程度上解释了结果的出现①Charles C.Ragin，Set Relations in Social Research:Evaluating Their Consistency and Coverage ，Political Analyssis，Vol.14，No.3，(Summer 2006)，pp.291-310.。在集合论上，如果某一条件或条件组合是某一结果发生的必要条件，那么，这些条件或条件组合的集合，就必然包含作为结果的集合。如果在20个案例或17个案例中都出现了导致结果发生的某一条件，我们就可以计算出其一致性程度为17/20=0.85。显然，一致性测量的分值越接近1，说明一致性程度越高，表明案例共享某一条件的程度也越高。在模糊集的分析中，如果案例中的某些条件或条件组合 (X)的一致性程度高，在集合上的表现就是，这些条件或条件组合的隶属度分数应该小于结果变量 (Y)。因为正是这些条件或条件组合导致了结果的发生，X是Y的w充分条件，在集合上的表示就是，X隶属于Y(即X＜Y)或者consistency(Xi≤Yi)=∑ (min(Xi，Yi))/∑ (Xi)。如果把这些变量之间的关系用坐标显示，则一致性程度高的表现就是X＜Y的案例应该在直角坐标系中主要位于Y=X的左上方。在拉金看来，如果一致性分数低于0.75，就可以认为不具有一致性。在实际操作过程中，那些一致性分数达到0.75以上的条件或条件组合，就可以编码为1;低于0.75的组合则编码为0。与此同时，一致性分数也可以用来确证某一具体条件是否构成结果发生的必要条件。如果X中的某一具体条件构成了结果发生的必要条件，则该条件的隶属度分数就应该大于结果的隶属度分数，即Consistency(Yi≤Xi)=∑ (min(Xi，Yi))/∑ (Yi)②Charles C.Ragin，Redesigning Social Inquiry:Fuzzy Sets and Beyond ，Chicago:The University of Chicago Press，2008，p.144.。

在某些条件导致结果发生的具体方式上，各个条件之间的多种组合方式都有可能导致结果的出现。此时，各个条件之间的每一种组合方式，都是导致结果发生的充分而非必要条件。而覆盖度分数所要测量的对象，正是各种条件的组合方式分别对结果发生的影响程度。例如，三个条件A、B、C的三种组合方式AC/AB/ABC，都导致了结果D的发生。如果导致D发生的影响力为1，则由ABC所构成的三种组合方式导致结果发生的影响力就形成了不同的比例。显然，导致结果发生的路径越多，就表明条件之间的组合方式越多，每个具体的路径的解释力所占的比例也就越小。由此可能带来的一个问题是，当一致性程度越高时，覆盖度分数可能就越低;反之，覆盖度分数越高时，一致性分数可能就越低。因此，在操作过程中的一个必然的要求就是，只有在先确定好一致性分数之后，再计算覆盖度分数。当AC、AB和ABC共同构成了结果D发生的三条路径时，这三条路径都应该有自己的覆盖度分数③Charles C.Ragin，Set Relations in Social Research:Evaluating Their Consistency and Coverage ，Political Analyssis，Vol.14，No.3，(Summer 2006)，pp.291-310.。

在由拉金等人开发的fsqca软件中，通过一致性分数和覆盖度分数的计算，就既可以获得各种条件或条件组合是否构成了结果发生的充分条件，还可以呈现出各种条件的组合导致结合发生的多条路径及其解释力①Fsqca的免费下载网址为:www.u.arizona.edu/～cragin/fsQCA，该网站同时还提供了操作手册和具体策略。。最近，经过完善的这一软件也可以作为清晰集的分析工具。

三、定性比较新策略的比较

如前所述，模糊集比较方法是在清晰集比较方法的基础上发展而来，而以布尔法为特征的清晰集方法又脱胎于传统的密尔法。但是，在传统的密尔法的基础上发展出来的新方法，则不仅仅是清晰集方法和模糊集方法;还有一种以清晰集为基础而发展出来的多值集合的定性比较(multi-valueQCA或mvQCA)的方法，也是一种与模糊集并行的方法。

首先应该注意到的是，这几种方法除了都以集合论作为自己的理论基础之外，还有一些在应用和功能方面的共同之处。这三种方法在政治科学和历史社会学研究中得到广泛应用的主要原因在于，在这两个领域所处理的变量中，有不少都不具宏观变量，事件发生的层次较高，因而在样本方面常常达不到统计分析所需要的数量要求。而这几种方法所要追求的目的，正是要充分结合案例导向的定性研究和变量导向的定量研究的各自优势，从而在传统的密尔法与定量研究之间，建立起一套综合性的分析模式。更为准确地说，清晰集 (csQCA)、多值集 (mvQCA)和模糊集(fsQCA)是三种站在案例导向的定性方法这一侧，但同时又充分吸收定量技术的一套比较方法②Benoit Rihoux and Charles C.Ragin，Configurational Comparative Methods:Qualitative Comparative Analysis(QCA)and Related Techniques，London:SAGE Publications Inc.，2009，p.6，pp.73-77.。在学术功能方面，这几种方法都致力于在案例和变量描述的基础上，检验现有的理论假设并致力于提出新的理论主张。但是，在具体应用方面，这几种方法又各有所长。

同样是作为清晰集分析的扩展方法，与模糊集不同的是，多值集方法并不是将变量的数值处理成0到1之间的隶属度分数，而是在清晰集的二分法基础上，对变量的数值进行多分。显然，这种方法相对于清晰集方法的直接优势，就是增加了变量的信息。而一旦将变量的数值进行多分之后，清晰集的二分法就只不过是多值集的多分法的一种特例了。换句话说，多值集在扩展二分法的基础上，将原来的清晰集拓展成了一种可以处理类别变量的方法。而且，如果再采用与统计分析中类似的虚拟变量 (dummy variable)的方法，同样可以将多值集纳入以布尔法为特征的清晰集的分析框架之中。同时，这种方法还可以通过分类的方式，将定距变量转化为类别变量而纳入模型之中③Benoit Rihoux and Charles C.Ragin，Configurational Comparative Methods:Qualitative Comparative Analysis(QCA)and Related Techniques，London:SAGE Publications Inc.，2009，p.6，pp.73-77.。由此引出的一些新的问题和技术，则可以通过专门处理多值集合的软件TOSMANA(Tool for small-n analysis)来进行操作④由德国政治科学家莱塞·克朗克齐斯特 (Lasse Cronqvist)开发出来的TOSMANA，免费下载地址为:www.tosmana.net。。

在德国政治科学家莱塞·克朗克齐斯特 (Lasse Cronqvist)开发出多值集方法及相应的操作软件之后，这种方法也得到了一些学者的重视。在笔者看来，多值集方法和模糊集方法都是在清晰集方法的基础上发展而来的，不过多值集方法并不需要依赖于概率标准来确定充分和必要条件⑤Lasse Cronqvist，Tosmana-Tool for Small-n Analysis.Version 1.0.Marberg:University of Marberg.www.tosmana.net.，2003.。有学者在比较了fsQCA和TOSMANA这两套软件的使用情况后认为，TOSMANA(2007)的用户界面更为友好，而且在文恩图 (Venn diagram)的可视化方面也要优于fsQCA。而在用途方面，则可以把多值集看作是清晰集和模糊集之间的一个中间状态。不过，由于清晰集和模糊集的应用都较为广泛，在理论上也更为成熟，而多值集在一些与集合论有关的理论和处理策略方面，则仍然还有值得讨论之处⑥Marrten P.Vink and Olaf Van Vliet，Not Quiet Crisp，Not Yet Fuzzy?Accessing the Potentials and Pitfalls of Multi-Value QCA，Field Methods，Vol.21，No.3，(Aug.2009)，pp.265-289.。从这些讨论中我们可以看出，清晰集、多值集和模糊集共同构成了以集合论为基础的一套比较策略，多值集和模糊集是由清晰集发展出来的两套并行策略，二者各有其适用领域。不过到目前为止，模糊集在社会科学中的应用范围要广于多值集。

随着模糊集方法的发展，还有一些学者在应用研究中尝试同时采用模糊集的方法和统计方法，在研究实践中对两种方法进行比较。卡兹 (Aaron Katz)等人在探讨1750年—1900年间讲西班牙语的拉美地区的大逆转现象 (早期处于边缘地位的殖民地后来成为富裕国家，早期处于中心地区的殖民地后来成为贫穷国家)的原因时，就同时采用了模糊集比较方法和回归分析的方法来检验各种假说。他们认为，模糊集比较方法的发现是:一个强大的自由派在概率意义上是经济发展的必要条件;密集的土著人口则在概率意义上是经济不发展的必要条件。但回归分析的发现则没有意义。因此他们认为，应该重视为模糊集比较的方法寻求因果关系①Aaron Katz，Matthias Vom Hau，James Mahoney，Explaining the Great Reversal in Spanish America:Fuzzy-Set Analysis Versus Regression Analysis ，Sociological Methods Research，Vol.33，No.4，(May 2005)，pp.539-573.。维斯 (Barbara Vis)则认为，虽然模糊集比较的方法和回归分析有着不同的认识论基础，但是，对于中等规模的大样本 (50—100个案例)，可以同时采用两种方法进行分析。为了检验这两种方法的差异，笔者选取了53个西方民主国家的政府投入劳工市场的支出状况进行研究。结果发现，模糊集比较的方法和回归分析都有自己的优势和不足，不过模糊集比较的方法更能够导向对结果发生的条件进行深入理解②Barbara Vis，The Comparative Advantages of fsQCA and Regression Analysis for Moderately Large-N Analysis.Sociological Methods＆ Research，Vol.41，No.1，2012，pp.168-198.。显然，这两个案例都表明，在样本的数量不是太大，变量的数目也不是太多的背景下，模糊集比较的方法确实更有利于深入发现某些导致结果发生的条件。但是，在案例和变量增多的情况下，回归分析无疑更有效力。

四、两个领域的新突破

通过将模糊集比较方法与其他比较方法的比较，可以进一步显现出模糊集方法的独特之处，尤其与统计方法相比的独特价值。不过，这里所指的统计方法，还主要是处理截面数据 (cross sectional data)的统计方法。如果结合纵贯数据 (Longitudinal data)的统计方法来与模糊集比较方法进行比较，就会发现，模糊集比较方法的一个重大缺陷，就是无法处理时间数据。而且，这一缺陷与模糊集方法声称要达到的目标之间，也构成了明显的紧张关系。这是因为，模糊集比较方法所要追求的目标，正是要通过相同条件的不同组合来解释导致结果发生的不同路径 (path)。但是，模糊集比较方法在实际操作中能够做到的，只能是将各种条件的交集、并集或补集视为不同的路径。而在各种条件的交集、并集和补集中，看不到某些条件的出场顺序的差异对结果是否发生所构成的影响。而模糊集的这一缺陷，同样存在于清晰集和多值集的比较方法之中。

所幸的是，两位学者的新近努力，构造出了一种可以处理时间顺序的模糊集比较方法，他们将这种方法称之为“时序性的定性比较分析”(Temporal Qualitative Comparative Analysis，TQCA)。在他们看来，传统的清晰集和模糊集分析虽然可以将条件和条件组合作为结果形成的各种路径，但并不能清楚地呈现出条件出现的先后顺序可能对结果产生的差异性影响。例如，在拉金的模糊集理论中，导致某一结果发生的条件组合A+B+C与A+C+B之间并没有区别，但在事实上，在A出现之后，B和C的出场顺序的差异完全有可能带来不同的结果。因此，在构造结果发生的条件组合时，必须要将事件出现的先后顺序纳入条件组合之中。其具体的操作方式是，在原来的表达式的基础上，用 “—”来表示事件出场的先后顺序。例如，A—B—C表示条件的出现顺序为ABC，而A—C—B则表示条件的出现顺序为ACB。除此之外，其他的所有操作原理都可以等同于原来的模糊集比较程序③Neal Caren and Aaron Panofsky，TQCA:A Technique for Adding Temporality to Qualitative Comparative Analysis，Sociological Methods＆ Research，Vol.34，No.2，(Nov.，2005)，pp.147-172.。实际上，模糊集分析的倡导者们在一定程度上也注意到了这一问题。他们认为，除了上述的途径外，还可以通过将条件组合进行细化或者将模糊集比较方法与其他方法相结合的方式，同样也可以处理集合分析中的时间性问题④Benoit Rihoux and Charles C.Ragin，Configurational Comparative Methods:Qualitative Comparative Analysis(QCA)and Related Techniques ，London:SAGE Publications Inc.，2009，pp.161-162.。

与拉金将模糊集理论应用到社会科学研究之中并发展出一系列QCA工具并行的另一条线索是，另外一些学者则一直在尝试将模糊集理论应用到政治学研究的各个领域。在国际关系领域，查尔斯·泰伯 (Charles S.Taber)早在1992年就曾经用模糊集理论来仿真美国对亚洲的外交政策①Charles S.Taber，POLI:An Expert System Model of U.S.Foreign Policy.American Political Science Review，Vol.86，No.4(Dec.，1992)，pp.888-904.。还有一些学者则曾经用模糊集理论来解释欧盟成员国在支持欧洲外交政策统一和安全政策中所体现出的差异性②Mathias Koenig-Archibugi，Explaining Government Preference for Institutional Change in EU Foreign Policy.International Organization，Vol.58，No.2，(Feb.，2004)，pp.137-174.。

在一些比较政治学家看来，模糊集理论对比较政治学的最重要的贡献，并不在于它为经验研究所作的贡献。在《模糊数学在比较政治学形式模型中的应用》一书中，克拉克 (Terry D.Clark)等人对模糊集理论在比较政治学中建立博弈模型进行了尝试。在模糊集的博弈理论者们看来，传统博弈论实际上是一种以清晰集为基础的博弈论。这是因为，在传统博弈论的博弈树中，参与方对于某一方案的策略性选择，要么为“选择”，要么为“不选择”，而现实中的情况则很可能是“非常倾向于选择”、“比较倾向于选择”、“不那么倾向于选择”和“非常不倾向于选择”等。这样，在博弈分析中，我们就完全可以借用模糊集的隶属度概念，将参与方的选择集作为模糊集来处理③Terry D.Clark，Jennifer M.Larson ，John N.Mordeson，Joshua D.Potter，Mark J.Wierman.，Applying Fuzzy Mathematics to Formal Models in Comparative Politics.Verlag:Spring，2008，p.22.。在该书中，克拉克等人正是运用这一基本原理，将传统比较政治学的一些博弈模型改造成模糊集的博弈模型。与此类似的是，阿弗里 (Badredine Arfi)也认为，以清晰集为基础的传统博弈论在构建真值表时只有“真”和“假”两种情况，而通过语言来进行策略性沟通时，不可避免地具有模糊性。这就导致传统的博弈论在这方面陷入了一个清晰与模糊之间的两难困境。要走出这一困境，其出路就在于打破清晰集的真假二分法，将真值细分为“非常正确”、“基本正确”、“基本错误”、“非常错误”和“错误”。同时，要允许各个选择类型之间出现交叉。这样，就可以将传统博弈论的策略转化为语言模糊策略，把参与方的偏好转化为语言模糊偏好，把推理的规则也转化为语言模糊推理，从而就可以把传统的博弈模型转换为语言模糊逻辑博弈模型。由此，传统博弈论所要寻找的纳什均衡也就变成了语言模糊均衡④Badredine Arfi.，Linguistic Fuzzy-Logic Game Theory.Journal of Conflict Resolution，Vol.50，No.1，(Feb.，2006)，pp.28-57.。

这两个方面的进展，无疑再次为模糊集比较方法的发展打开了新的视野。前者通过顺序符号的引入，使得模糊集比较的方法可以纳入历史比较分析的一切范畴。后者通过对传统博弈论的改造，为模糊集比较开启了演绎的通路。

五、问题与前景

与传统的清晰集合理论相比，模糊集理论的首要特征，就是通过隶属度概念和测量工具的引入，将传统的二分逻辑转换成了定比数据，从而大大提高了量化水平。但正是在将原始数据转换为隶属度分数这个问题上，模糊集分析却一直存在着难以解决的矛盾。从理论上讲，任何原始数据，都可以依据某种标准转换为［0，1］之间的隶属度分数。关键在于，到底应该依据何种标准将特定的数值转换为［0，1］之间的某一具体数值?在模糊集理论的发展和应用史上，学者们曾经尝试过各种方法，试图建立起一套能将原始数值转换为隶属度分数的标准。目前已经发展出的转化方式就可区分为形式论、概率论、决策论和公理化方法。虽然研究者在实践中可以选择或组合使用这些方法，但从理论上讲，没有哪一种方法可以在理论上充分证明，这种方法是完全正确的⑤［加］约翰·福克斯:《社会科学中的数理基础及应用》，吴晓刚主编，格致/上海人民出版社2011年版，第306页。。拉金则认为，研究者应该根据自己对研究领域的实质性理解或现有的理论知识来确定转换的标准①Charles C.Ragin ，Redesigning Social Inquiry:Fuzzy Sets and Beyond ，Chicago:The University of Chicago Press，2008，p.86.。问题在于，这两种方法实际上都还是有主观性的方法。在研究者对某一领域的理解存在实质性差异和有关理论本身有争论的情况下，研究者在确定这一标准时就会面临更大的挑战。因此，在这个问题上，无论研究者选择哪一种策略，实际上都存在着某种风险。

与此同时，在用逻辑真值表进行分析时，所有的以布尔法为代表的集合分析都适用的一个原则是，从理论上讲，对K个条件的分析就应产生出2K个案例。但在实际研究过程中，当条件数量增加到一定程度，再加上条件组合，研究者就很难收集到众多的案例，有的案例甚至在现实中就根本不可能出现。此时，集合论的分析就存在一个逻辑剩余的问题。对此，清晰集、多值集和模糊集都是采用一个“最小化 (minimization)”的策略来进行简化处理这些在现实中不存在的案例及其条件组合。在一些学者看来，对于那些在现实中根本无法观察到的条件组合进行这种推理，存在着极大的理论风险，并且有可能将研究者带入一种对想象的状态进行研究的情形②John Markoff，A Comparative Method:Reflections on Charles Ragin's Innovatins in Comparative Analysis，Historical Methods，Vol.23，No.4(Fall 1990)，pp.177-181.。不过，在集合论比较的支持者看来，这种状况则更能体现清晰集和模糊集研究的优势。这是因为，正是通过这种途径，才使集合论的研究超越对可观察事实的有限研究，并基于可观察的事实而推导出超越既定事实的理论。因此，这一特点并不是模糊集分析的缺陷，反而是它的优势③Benoit Rihoux and Charles C.Ragin，Configurational Comparative Methods:Qualitative Comparative Analysis(QCA)and Related Techniques ，London:SAGE Publications Inc.，2009，pp.152-154.。

当然，问题的存在并不意味着其发展的停滞。除了继续开发新的工具和技术外，模糊集比较分析的理论家一边在将模糊集比较方法与其他方法进行比较，一边还尝试将模糊集比较的方法与其他方法结合使用。例如，为了提高研究成果的可靠性，一些学者还曾经尝试过，在同一项研究中同时采用定量统计和定性比较分析的方法。例如，在研究社会运动时，有些学者就曾经采用过将时间序列截面数据分析和定性比较分析相结合的方法④Edwin Amenta and Sheera Joy Olasky，Age for Leisure?Political Mediation and the Impact of the Pension Movement on U.S.Old-Age Policy ，American Sociological Review，June 2005，Vol.70，No.3，pp.516-538.。在国内的研究中，黄荣贵和桂勇已经将早期的定性比较分析用于互联网与业主集体抗争的研究之中⑤黄荣贵、桂勇:《互联网与业主集体抗争:一项基于定性比较方法的研究》，《社会学研究》2009年第5期。。何俊志和王维国也曾经利用北京市各郊区乡镇人大的宏观资料，考察了乡镇人大的代表结构与履职绩效间的关系⑥何俊志、王维国:《代表结构与履职绩效——对北京市13个区县的乡镇人大之模糊集分析》，《南京社会科学》2012年第1期。。

总之，只要存在可比较的案例，作为一种小样本比较的方法，模糊集比较方法已经在演绎和归纳这两种层面上奠定了研究基础，形成了一系列研究成果，并且与其他的研究方法展开了对话。模糊集比较方法的单独或联合使用，必将会在一些领域内得到新的应用。