Lagrange 系统的Lie 对称性与动力学逆问题

梅凤翔，李彦敏

(1.北京理工大学 宇航学院，北京 100081;2.商丘师范学院 物理与电气信息学院，河南 商丘 476000)

0 引 言

20世纪60年代以来，动力学逆问题有了一般的数学提法.目前，动力学逆问题已成为星际航行学，火箭动力学，规划运动理论中的基本问题.专著［1，2］对动力学逆问题的提法和解法给出较全面的论述.本文研究Lagrange 系统的Lie 对称性与动力学逆问题.1979年Lutzky 首先将Lie 对称性引入力学系统守恒量的研究［3］.文献［4－6］研究了各类约束力学系统的Lie 对称性导致的守恒量.对Lagrange 系统与Lie 对称性相关的正问题是指，对给定的Lagrange 函数，如果Lie 对称性的无限小生成元满足某个结构方程，则可导出系统的守恒量.与Lie 对称性相关的动力学逆问题是指，对给定的守恒量(积分)，反过来构造Lagrange函数，并给出发生Lie 对称性的无限小生成元以及规范函数.

1 Lie 对称性与动力学正问题

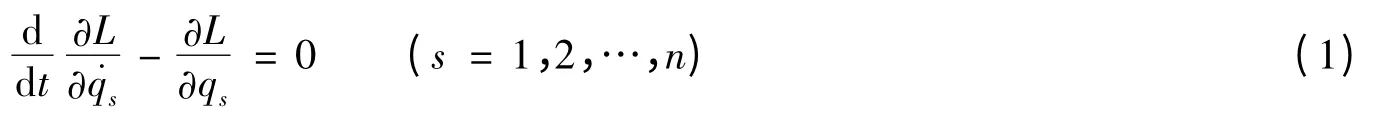
Lagrange 系统的微分方程表为完整保守系统，广义力有广义势的系统，Lagrange 力学逆问题系统等，其微分方程可表为形式(1)［6］.假设系统(1)非奇异，即设

则由方程(1)可解出所有广义加速度，简记作

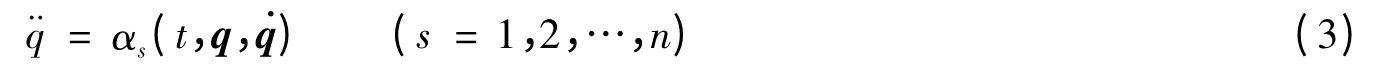
引入时间和坐标的无限小变换

其中ε 为一无限小参数，ξ0，ξs为无限小生成元.方程(3)Lie 对称性的确定方程表为

其中

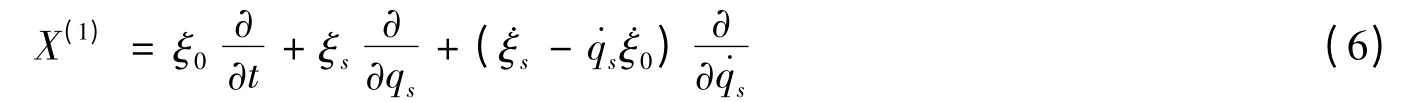
如果无限小生成元ξ0，ξs满足方程(5)，则相应对称性为Lie的.如果Lie 对称性的生成元ξ0，ξs和规范函数GN满足如下结构方程［6］

则Lie 对称性导致守恒量

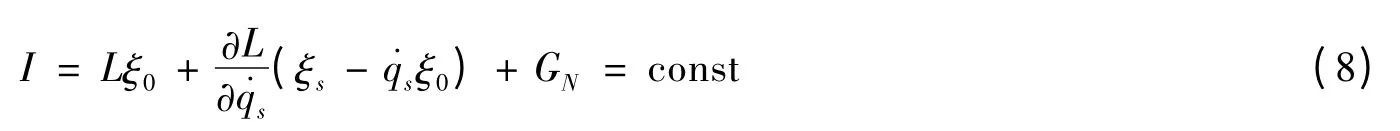
与结构方程(7)相应的Killing 方程为

因此，如果无限小生成元ξ0，ξs和规范函数GN满足Killing 方程(9)，(10)，则Lie 对称性导致守恒量式(8).

2 Lie 对称性与动力学逆问题

对Lagrange 系统，与Lie 对称性相关的动力学逆问题的提法如下:

给定Lagrange 系统的一个积分需要确定系统Lagrange 函数L，以及Lie 对称性的无限小生成元ξ0，ξs和规范函数GN.

为解上述逆问题，首先，令积分(11)等于Lie 对称性导致的守恒量I，即令

它给出L，ξ0，ξs和GN的一个关系.其次，按Lie 对称性逆问题，由积分给出生成元［6］

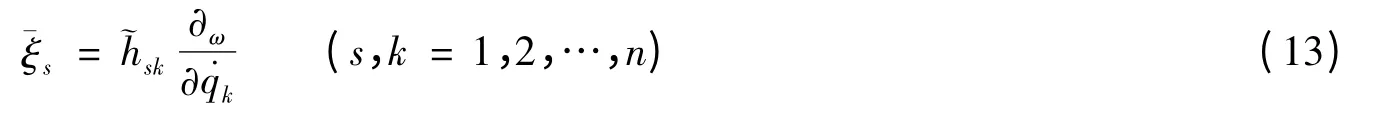
其中

它给出L，ξ0，ξs的n个关系.第三，利用Killing 方程(9)，(10)，给出L，ξ0，ξs，GN的(n+1)个关系.最后，需验证所得无限小生成元ξ0，ξs是否Lie的.文献［7］已证明，对Lagrange 系统，Noether 对称性必是Lie 对称性.因此，这一步骤可以省略.

与Lie 对称性相关的动力学逆问题的解，与一般动力学逆问题的解一样，一般说来不是唯一的，而是一个解集.

3 算 例

已知单自由度Lagrange 系统的一个积分

试求Lagrange 函数L，Lie 对称性的生成元ξ0，ξ 以及规范函数GN.

将式(14)代入(13)，得到

将式(14)～(16)代入(12)，得

由此得

此时Killing 方程(10)自动成立.将式(15)～(17)代入Killing 方程(9)，得到

它有解

这样，就得到逆问题的一个解

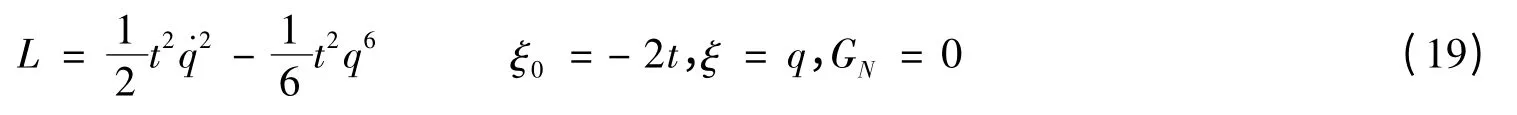
问题还有其他解，例如

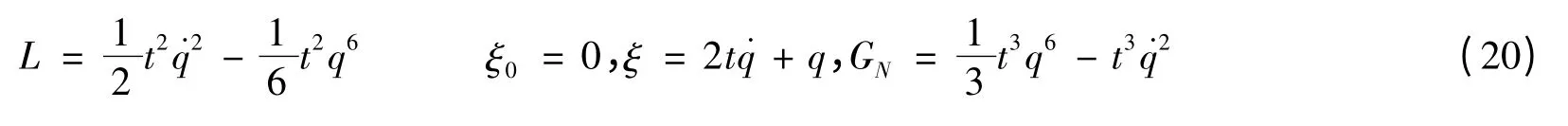
4 结 论

Lagrange 系统是一类重要而常用的约束力学系统.动力学逆问题是一个既有理论又有应用的动力学问题.本文对Lagrange 系统，给出与Lie 对称性相关的动力学逆问题的提法和解法，主要结果为求解逆问题的基本公式(5)，(9)，(10)，(12)，(13).对其他约束力学系统也可进行类似讨论.

［1］Galiullin AS.Methods of solution of inverse problems of dynamics［M］.Moscow:Nauka，1986 (in Russian).

［2］梅凤翔.动力学逆问题［M］.北京:国防工业出版社，2009.

［3］Lutzky M.Dynamical symmetries and conserved quantities［J］.J Phys A:Math Gen，1979，12(7):973－981.

［4］赵跃宇，梅凤翔.关于力学系统的对称性与不变量［J］.力学进展，1993，23(3):360－372.

［5］赵跃宇，梅凤翔.力学系统的对称性与不变量［M］.北京:科学出版社，1999.

［6］梅凤翔.李群和李代数对约束力学系统的应用［M］.北京:科学出版社，1999.

［7］梅凤翔.约束力学系统的对称性与守恒量［M］.北京:北京理工大学出版社，2004.