线性变换下的三维刚体运动

王塞楠

(浙江师范大学 数理信息工程学院，浙江 金华 321004)

0 引 言

1 主要结果

在文献［1］中的命题给出了在坐标变换下，结构矩阵的变换公式.

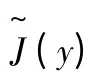
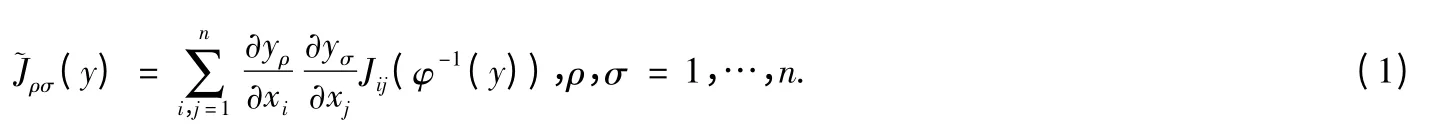
若令C=AT，则C的元素是cij=aji，j，i=1，…，n.则(1)为

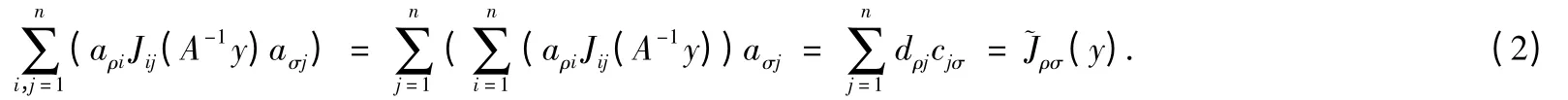
如果我们将可逆的线性变换y=Ax 作用于广义Hamilton 系统(3)，A 是可逆矩阵

则(3)变成

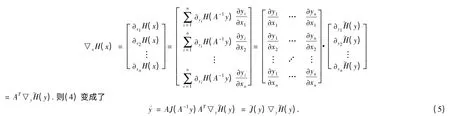
在下面的研究中，我们只考虑n=3的情形，取B=A－1，从而φ－1(y)=By.利用(1)，我们得到了一个新的结构矩阵.

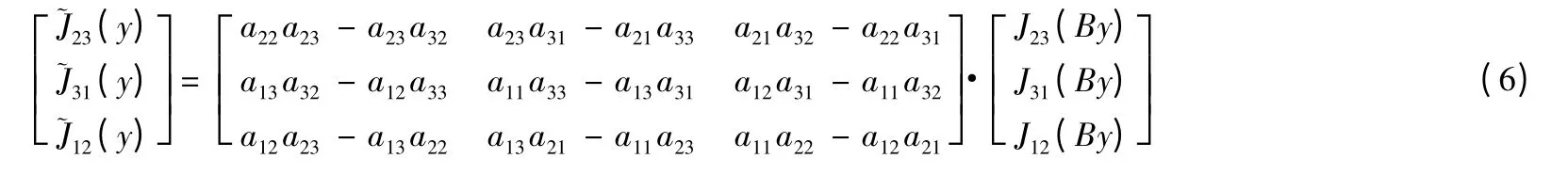
通过观察，可知

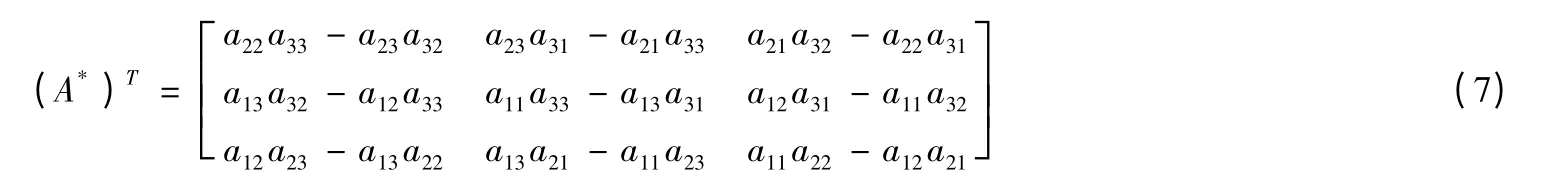
其中A*是A 伴随矩阵.

如果我们以三维的刚体运动作为例子［2］，［3］，则可知其结构元素分别为J12=x3，J13=－x2，J23=x1，那么

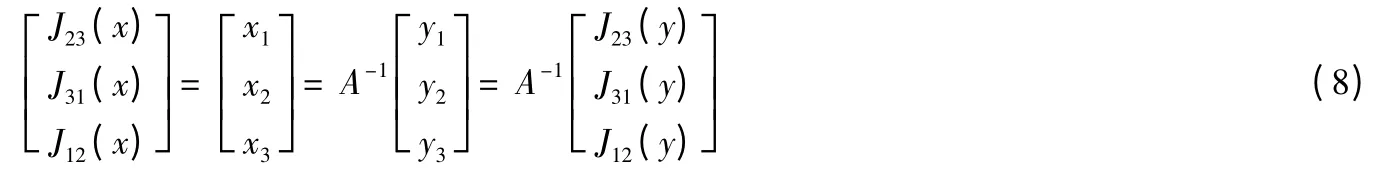
因此(6)变成了

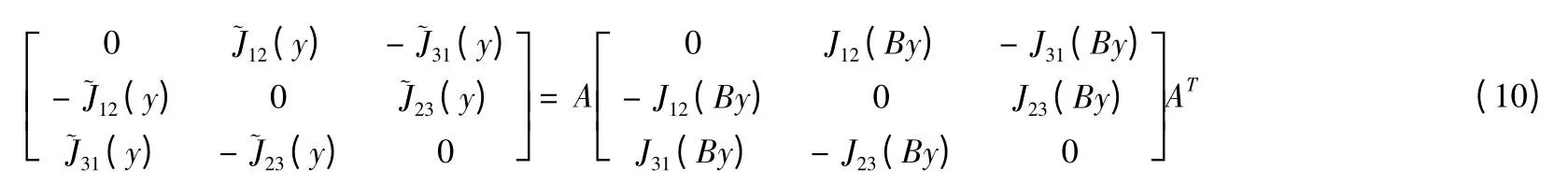
对于三维刚体的运动，我们发现:

注:det(A)表示矩阵A的行列式.

［1］李继彬，赵晓华，刘正荣.广义哈密顿系统理论及其应用(第二版)［M］.北京:科学出版社，2007.

［2］Metin Gürses，Gusein Sh.Guseinov，Kostyantyn Zheltukhin，Dynamical systems and Poisson structures［J］.Journal of mathematical physics，2009，50，112703:1－9.

［3］Ahmet Ay，Metin Gürses.Kostyantyn Zheltukhin，Hamiltonian equations in R3［J］.Journal of mathematical physics，2003，44:5688－5705.