基于数据驱动的发电机组软测量建模方法优化研究

陈凯亮，陈坚红，盛德仁，李 蔚

（浙江大学 热工与动力系统研究所，浙江 杭州 310027）

0 引 言

现代大型火力发电机组的控制和优化决策依赖于测量数据的准确性，而在工程实际中，要做到参数的准确测量是不容易的，有一些参数（如燃气轮机的压气机进气流量等）是很难准确测量的；另一类参数（如汽轮机排汽湿度等）是无法直接测量的；而且很多测量传感器是工作在高温、高压、易腐蚀的复杂环境下，受到电磁干扰，测量数据的准确与否难以保证。

针对以上问题，研究者们主要采用基于机理分析结合数据驱动建模的方法建立测量参数间的近似模型，用可测量准确的变量估计测不准和无法直接测量的变量，或进一步用这个模型检测测量数据的有效性。

目前，基于数据驱动的软测量建模方法主要包括主元分析法（Principal component analysis，PCA）、偏最小二乘方法（partial least square，PLS）和神经网络方法（neural netword，NN）等，这些方法各有优点和局限，PCA和PLS利用信息压缩技术将高维数据降维简化数学模型，特别适用于处理相关性强的数据，但对非线性问题处理能力不强。径向基神经网络（radial basic functimneural netword，RBFNN）具有良好的非线性逼近能力，而且训练过程中不易陷入局部极小的解域中，特别适用于非线性建模，但存在复杂网络训练时间长、不易收敛等问题。

近年来，针对以上方法存在的缺陷，学者们做了很多研究，并进行了不同程度的改进。如文献［1－2］提出的递归偏最小二乘法（RPLS）适用于非线性建模和动态建模问题。文献［3］提出的基于自联想神经网络（AANN）的自校正数据检验方法通过对神经网络输入数据的处理与选择，提高了神经网络方法在线应用的准确率。文献［4］将最小二乘支持向量机与自适应遗传算法相结合，提高了模型的精度和预测能力。

尽管通过各类方法的组合优化，基于数据驱动的软测量建模方法已日趋成熟，但在实际应用的过程中仍存在不少问题。如王惠文［5］提出的基于样条变换的PLS方法有效解决了PLS方法非线性拟合能力差的问题。但该方法在建模时，相关参变量的选取是经机理分析定性得出的，研究者未考察变量间依赖关系大小，而全部引入模型中，因此会导致模型因引入相关性不强的变量而相当复杂，拟合效果不佳。刘波平等［6］提出了将PLS与广义神经网络（GRNN）结合的方法，即利用PLS数据压缩提取主成分，将主成分作为神经网络的输入，从而有效地简化了神经网络模型，提高了训练速率和模型的可靠性。但这种方法实际上并未真正实现变量的筛选工作，主成分中仍然包含相关性不强的参变量的相关信息。王建星等［7］将GRNN与平均影响值（MIV）结合的方法用于机组主蒸汽流量的测定，通过评比待建模变量与参变量的相关程度，有效地筛选了变量，并得到了较准确的神经网络模型。但由于GRNN神经网络模型参数的数量随着训练样本数的增加而爆炸式地增加，给存储模型的数据库的运行和维护带来极大困难，尤其在发电机组系统中同时存在成百上千的测点需要软测量或检测测量数据的准确性，模型存储和维护成本必然会影响该方法的实际应用。

针对以上方法存在的不足，本研究提出基于GRNN和B样条PLSR的融合建模方法，下文简称NN－PLS方法。NN－PLS方法采用非线性拟合能力较好的GRNN预建模，计算机理分析初步选定的参变量对因变量的平均贡献率，然后将筛选出的主要参变量采用B样条PLS建模后得出最终简化的非线性模型。这样充分利用了GRNN优秀的非线性拟合能力完成了变量筛选，同时采用模型结构相对简单但拟合能力同样优秀的PLS完成最终建模，可有效规避保存GRNN模型海量参数给机组监控系统及数据库的运行和维护带来的麻烦。

本研究先介绍GRNN建模及筛选变量的原理及特性，再给出B样条PLS的建模理论，然后说明所提出的NN_PLS建模方法的实现过程，最后通过算例验证该方法的经济性和有效性。

1 GRNN建模理论

1.1 GRNN的拓扑结构

广义神经网络（GRNN）是一种基于非线性回归理论的前馈式神经网络模型。GRNN具有很强的非线性映射能力和柔性网络结构以及高度的容错性和鲁棒性，适用于解决非线性问题。GRNN的拓扑结构如图1所示，包括输入层、模式层、求和层、输出层。输入层节点数量为自变量参数个数p，模式层节点数量为训练样本数n，求和层节点数量比因变量参数个数k多1个，即k+1个，输出层节点数量为因变量参数个数k。

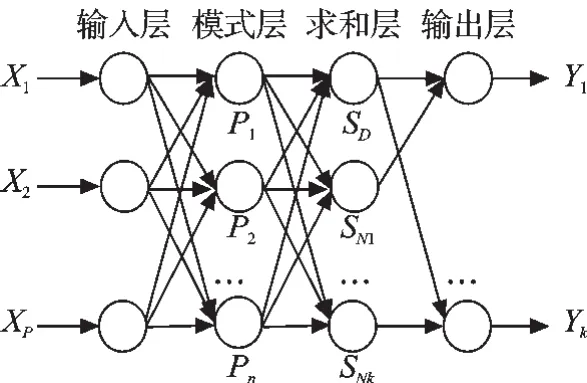
图1 广义回归网络结构图

GRNN的优势在于当训练样本数目很大时能够快速学习并收敛到样本积聚最多的最优回归平面，并且可以处理不稳定的数据。然而由GRNN的拓扑结构可知，训练好的GRNN中权值、阈值参数的个数随着样本数的增加而急剧增加，仅输入层至模式层的个数就有p×n+n个，假若对于p=8,n=50的模型，仅前两层参数个数就为450个，要在发电机组监控系统中保存并维护成百上千个这样的模型，显然极为困难。因此，采用GRNN方法建立的模型不适合用于在线的软测量及数据验证等应用。但鉴于GRNN神经网络非线性拟合能力强、收敛快的优势，可以采用GRNN预建模，考察由机理分析初步选定的自变量参数对因变量参数的影响值，从而筛选出主要的建模参数，使后续建立的模型得到简化。

1.2 基于GRNN的MIV相关变量筛选

预建模时，本研究将机理分析得出的输入输出样本输入到GRNN中，采用循环训练［8］的方法确定合理的网络分布密度使GRNN收敛，并达到最佳的预测效果。

网络训练终止后，本研究将训练样本P中每一个参变量特征在其原值的基础上分别±10%构成新的两个训练样本P1和P2，将P1和P2分别作为仿真样本利用已建成的网络进行仿真，得到两个仿真结果A1和A2，求出A1和A2的差值，即为变动该变量后对输出产生的影响变化值（IV），最后将IV按样本数平均得出该参变量对于因变量的MIV。最后本研究根据MIV［9］绝对值的大小为各参变量排序，得到各参变量对网络输出影响的相对重要性位次表，从而判断出输入特征对网络结果的影响程度，即实现了变量筛选。

1.3 基于B样条变换的PLS建模

偏最小二乘回归（PLSR）是一种将主成分分析、典型相关分析以及多元线性回归相结合的回归建模方法。该方法能够同时提取输入变量和输出变量数据中数据的变化信息，选择对数据累积方差最大的主元数目，使得输入变量和输出变量间的相关程度达到最大［10］。 PLS在参变量存在严重多重相关性及样本个数较少的线性系统建模过程中优势明显。

而发电机组系统存在非线性关系，采用线性PLS建模无法取得令人满意的结果，本研究选用拟线性的方法来解决非线性问题。样条变换采用了分段拟合的思想，可以按需要裁剪以适应任意曲线的连续变化，拟合曲线对原始数据的特异点并不敏感，这使得模型在排除原始数据噪声方面效果较好。

基于样条变换的偏最小二乘回归建模就是将自变量与因变量之间的未知非线性关系按照各维自变量对因变量的拟线性关系相加展开，再进行偏最小二乘回归求参，从而得到自变量对因变量的整体函数解析式。

设待建模型有p个自变量{x1,x2,…,xp}和一个因变量y，选取n个样本点构成自变量与因变量原始数据表X=[x1,x2,… ,xp]n×p和Y=[y]n×1。自变量和因变量的非线性关系式可表示为：

式中：β0—常数项，fj(xj)—自变量xj对因变量y的非线性关系，ε—随机误差项。

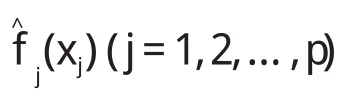
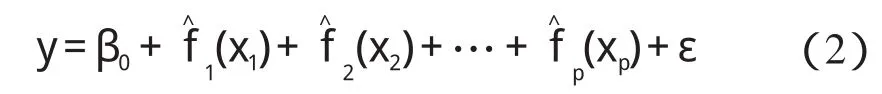
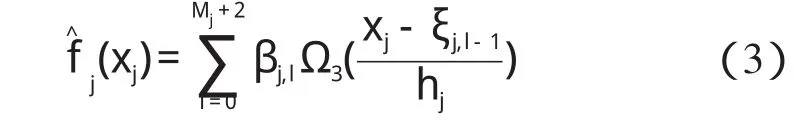
式中：Mj—第j个变量的样条变换分段数；β0,βj,l—模型的待定参数。

由式（2，3），可得到自变量和因变量的非线性关系式为：

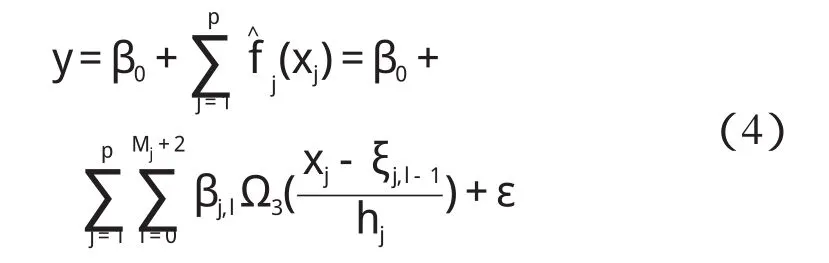
在式（4）中，y与zj,l=Ω3((xj-ξj,l-1)/hj)呈线性关系，可以采用偏最小二乘方法求解模型。

相对于GRNN神经网络模型，B样条PLS模型的参数较少，与样本数n无关，对于p=8,n=150的训练样本，参数个数仅为80个，且不随n增加而增加。因而相对于GRNN模型更易保存在数据库中，适用于各种在线应用。

但由于发电机组运行参数之间关系的复杂性，研究者通过机理分析很难确定模型的参变量与待建模变量相关性强弱的定量关系，很难在模型的完备性、性能和模型的复杂性、计算量等代价之间作取舍。为了得到完备的模型，由机理分析初步选定的参变量常常含有相关性不强的冗余变量，如果不在B样条PLS建模前进行变量筛选，那么最终得到的模型将因含有这部分信息而更加复杂，且拟合性能下降。因而研究者为了得到完备、精确、简化的模型，有必要在B样条PLS建模前，对由机理分析初步选定的参变量进行筛选。

2 基于NN－PLS的数据驱动建模方法

对于发电机组等复杂非线性系统，本研究所要建立的软测量模型应适应各个典型工况（不同负荷、春、夏、秋、冬等），因而必须使用大数量的样本训练，模型性能才能符合实际。而GRNN神经网络训练样本数不宜过多，否则需要保存在数据库中的参数将随着样本数的增加而爆炸式的增长。当训练样本数较少时，虽然对部分数据仍能取得较好的拟合效果，但由于神经网络的泛化能力较弱，对于与训练样本相差较大的数据预测效果较差。所以GRNN不适宜用来建立最终在线应用的模型。但GRNN的优点在于非线性拟合能力强，利用Matlab软件可以方便地用于对样本数据建模并考察建模参变量的影响值，实现变量筛选。而B样条PLS方法采用拟线性的方法解决非线性的问题，虽然最终得到的模型泛化能力较好，且结构简单，参数少，但由于建模过程较为复杂，该方法无法在建模的同时实现变量筛选，常常因引入很多相关性不强的变量使模型精度下降。

结合两者的优势，本研究提出了NN－PLS建模方法，建模流程图如图2所示。

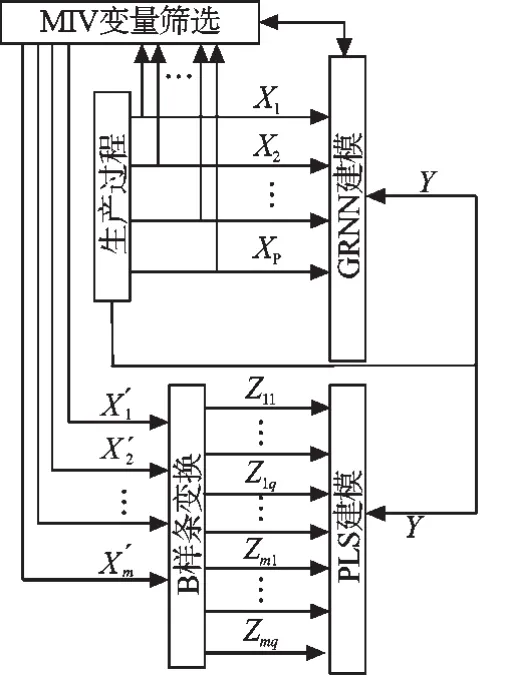
图2 建模流程图

在对变量Y建模时，首先，本研究采用机理分析方法定性地得到对测量数据Y建模需要的全部相关参变量X1～XP，然后选取合适的样本数据建立GRNN模型，应用该GRNN模型考察模型中每个参变量对因变量Y的MIV值以筛选出主要变量X'1～X'm，将筛选出的变量重新构成样本空间，进行三次B样条变换，从而将自变量空间X'非线性映射到PLS自变量空间Z中，然后进行PLS建模求取Y对Z的回归方程，并可以还原得到Y对X'的回归方程，该模型即为最终的简化模型。NN－PLS不但利用了采用大量样本训练时GRNN预建模在复杂非线性问题中能够迅速收敛，且进一步与MIV方法结合，可以方便地定量筛选出建模所需要的主要参变量的优势，弥补了“PLS建模过程复杂，常因无法对机理分析初步选定的变量定量筛选而导致模型中引入部分相关性不强的变量从而使模型性能下降”的劣势，而且研究者采用结构简单、参数少且泛化能力较好的B样条变换拟线性PLS方法将筛选变量建模，得到了精度、泛化能力、结构都十分理想的模型，有效解决了“GRNN建模因大量样本训练而导致参数过多，从而不易用在需要保存模型的各种在线应用中”的问题。

本研究显示Lp-PLA2及hsCRP的浓度变化有助于客观有效的判定颈动脉粥样硬化的治疗效果。但样本量少，仍需更多大样本的研究。

3 NN－PLS建模方法的验证与应用

虽然本研究阐述的建模方法以测量测不准变量、无法直接测量变量和验证数据有效性为目的，但为了验证该方法的有效性，现笔者选取测量较为准确的功率测点加以验证，以某联合循环电厂4#机组（400 MW）燃机有功功率数据建模为例，根据联合循环电厂系统结构的热力分析，同时考虑到燃机有功功率与相关热力参数之间的关系，初步选取大气温度、大气压力、燃机扩散控制阀阀位、燃机预混控制阀阀位、燃机值班控制阀阀位、燃机IGV开度、压气机进口压差、压气机出口压力、压气机进口温度、燃机值班气流量、燃机排气温度1B、燃机排气温度5B、燃机排气温度9B、燃机排气温度13B、燃机排气温度17B、燃机排气温度21B共16个参数作为模型的输入变量。

训练样本的选取是影响模型性能的重要因素，样本数不宜过少，否则无法满足训练要求；而样本数过多又会导致过拟合，影响模型的泛化能力。同时更重要的是选取的样本要分布均匀，是各工况下的典型数据，以使所建模型泛化性能较好。本研究选取的训练样本覆盖了春、夏、秋、冬，温度从－5℃～35℃，大气压力从99 kPa～104 kPa，功率负荷段从30%～100%之间的共150组典型运行工况数据。

3.1 广义神经网络MIV筛选相关变量

在构建神经网络之前，为了避免由于输入变量物理意义及单位不同而对神经网络模型及相应MIV值的影响，本研究首先对各变量进行归一化处理，即：

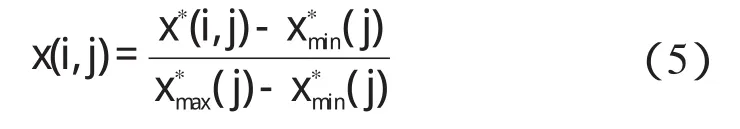
式中：x∗(i,j)—第j个变量的第i个样本值；(j)，(j)—第j个变量的最大、最小值；x(i,j)—变量特征归一化序列。

本研究在Matlab R2009b下编制神经网络训练程序，实现基于MIV的变量筛选，最终得到各输入变量的平均影响值。

16个变量的平均影响值（MIV）绝对值分布如图3所示，对其排序后，选取占MIV绝对值总和前85%的变量作为模型输入变量，其MIV（绝对值）大小分别为0.02、0.017 4、0.017 3、0.006 8、0.006 4、0.006 2、0.005 2、0.005 1。分别代表：压气机出口压力、燃机排气温度13B、燃机排气温度5B、燃机值班气流量、大气温度、燃机排气温度9B、燃机IGV开度、压气机进口温度，这8个变量平均影响值占总体影响值87.03%。

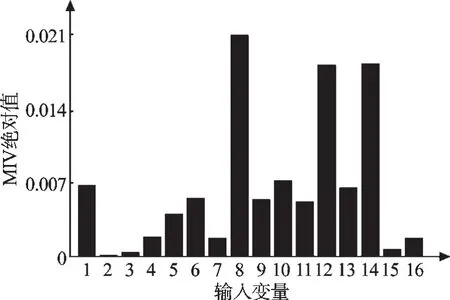
图3 各变量平均影响值图

3.2 基于样条变换的偏最小二乘回归建模

本研究筛选出的8组自变量和因变量燃机有功功率的原始数据共同构成了样条变换偏最小二乘回归建模的原始样本数据。

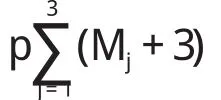
在对标准化的PLS自变量空间Z~和因变量Y~建模时，根据交叉有效性原则，本研究提取了6个主成分，最终得到的模型中因变量Y对PLS自变量空间Z的回归系数。

PLS模型各变量回归系数图如图4所示。

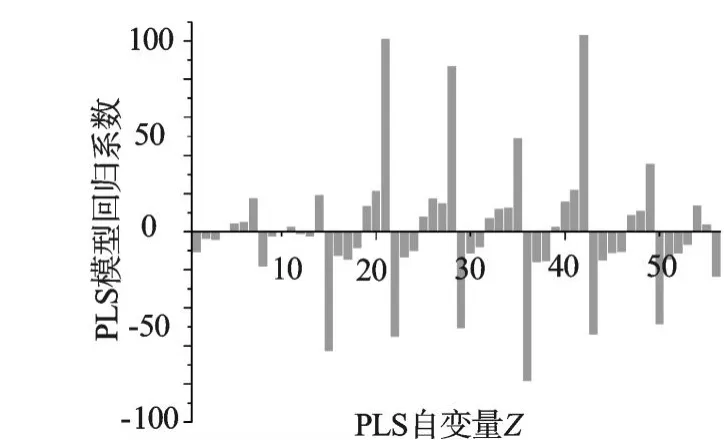
图4 PLS模型各变量回归系数图

3.3 NN-PLS模型的适用性和精度

模型的适用性需要考察模型预测值和因变量实际样本值之间的预测误差，为了考察该模型的适用性，本研究另外选取对应9组建模变量的50组典型数据作为测试样本，并对其进行样条变换，然后用已建好的PLS模型对其进行预测，预测结果如图5所示。

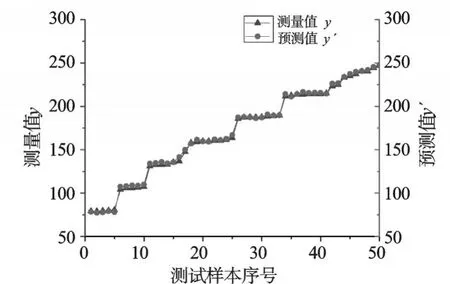
图5 各样本点样本值和预测值拟合关系图

从图5中可以看出，在不同的负荷段模型预测值与样本值均基本重合，预测效果十分理想。

此外，为了比较NN－PLS与GRNN建模的预测效果，本研究使用前述150组数据作为训练样本，分别采用两种方法对经筛选变量后的9组变量建模，并另外选取5组测试样本分别比较两者的预测性能及精度，结果如表1所示。

从表1中可以看出，在不同负荷工况下，NN－PLS的预测相对误差均低于1%，与GRNN的预测精度相近，某些点甚至更好。同时，由于测试样本选取的是未经训练过的不同负荷段上的样本，经模型预测，效果均十分理想，证明NN－PLS模型能同时满足精度和泛化能力的要求。

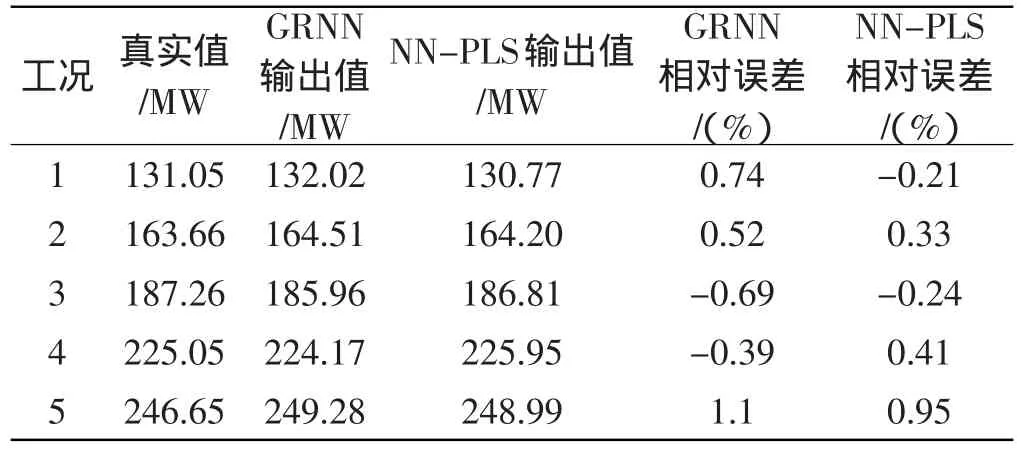
表1 模型拟合结果对比表

虽然采用大量样本训练的GRNN在变工况下同样能取得较好的预测效果，但笔者注意到此时的模型参数仅GRNN输入层至模式层的权值参数已经多达150×8=1 200个，这样复杂的模型对于难测参数软测量及校验实时测量数据准确性等在线应用是不可取的。而相比GRNN神经网络而言，NN－PLS在保证了模型性能和精度的同时，需要保存的模型参数仅为回归系数56个，B样条变换的参数24个，总计不足百个，大大简化了模型，对于在线应用优势明显。

4 结束语

本研究提出了融合GRNN与B样条PLS优势的NN－PLS数据驱动软测量建模方法，用以解决发电机组等复杂系统中难测准数据的软测量或已测量数据的有效性验证的问题。GRNN预建模考察机理分析初步选定的参变量对因变量的影响值，筛选出主要建模变量。B样条PLS对筛选出的变量建模得出的最终模型不但结构简单、参数少，而且预测精度和泛化能力都较好。

本研究采用某联合循环电站的校准后的实测数据验证该建模方法，研究结果表明NN－PLS方法建立的模型能很好地拟合出不同工况下的测量值，其精度与得到充分训练的GRNN神经网络模型相当，且由于NN－PLS模型本身结构简单、参数较少，更加适合用于发电机组系统中难测参数的软测量及已测量数据准确性的实时校验等在线应用中。

（

）：

［1］LI C，YE H，WANG G.A recursive nonlinear PLS algorithm for adaptive nonlinear process modeling［J］.Chemical Engineering and Technology，2005，28（2）：141－152.

［2］苏金明，李春富，孙如田，等.递推PLS方法及其在过程监控中的应用［J］.机电工程，2010，27（3）：93－95，99.

［3］司风琪，徐治皋.基于自联想神经网络的测量数据自校正检验方法［J］.中国电机工程学报，2002，22（6）：152－155.

［4］尚万峰，赵升吨，申亚京.遗传优化的偏最小二乘支持向量机在开关磁阻电机建模中的应用［J］.中国电机工程学报，2009，29（12）：65－69.

［5］王惠文，黄海军，苏建宁.基于样条变换的PLS回归的非线性结构分析［J］.系统科学与数学，2008，28（2）：243－250.

［6］刘波平，秦华俊，罗 香，等.PLS－GRNN法近红外光谱多组分定量分析研究［J］.光谱学与光谱分析，2007，27（11）：2216－2220.

［7］王建星，付忠广，靳 涛，等.基于广义回归神经网络的机组主蒸汽流量测定［J］.动力工程学报，2012，2（2）：130－134.

［8］傅荟璇，赵 红.Matlab神经网络应用设计［M］.北京：机械工业出版社，2010.

［9］GEORGE D，PARTHA N，JONATHAN S，et al.Prediction of rib fracture injury outcome by an artificial neural network［J］.Journal of Trauma-Injury Infection&Critical Care，1995，39（5）：915－921.

［10］BASTIEN P，VINZI V E，TENENHAUS M.PLS generalized linear regression［J］.Computational Statistics&Data Analysis，2005，48（1）：17－46.