含参变量的拉普拉斯逆变换及其应用
符云锦
(凤凰县两林学区,湖南凤凰 416211)
1 背景知识
文〔1〕给出了含参变量的拉普拉斯变换的定义如下。
定义 设函数f(t)在区间[λ,+∞]上有定义,如果含参变量s,λ的无穷积分对s的某一取值范围是收敛的,则称无穷积分

为函数f(t)的含参变量λ的拉普拉斯变换。f(t)称为原函数,称为象函数,并记作。同时,含参变量λ的拉普拉斯的逆变换记作
要注意的是在(1)式中,参数λ和变量s均可以为复数。同时,文〔1〕中还给出了含参变量的拉普拉斯变换的存在性和基本性质,利用含参变量的拉普拉斯变换导出了一些常用函数的含参变量λ的拉普拉斯变换表达式。本文对含参变量的拉普拉斯变换的逆变换进行了研讨,得出其唯一性和相关性质,并举例说明其应用。
2 含参变量λ的拉普拉斯逆变换的性质
与拉普拉斯逆变换〔2-4〕一样,含参变量的拉普拉斯逆变换同样具有相应的性质。
性质1(唯一性定理)若给定一个关于s,λ的函数F(s,λ),则存在唯一的函数f(t)使得
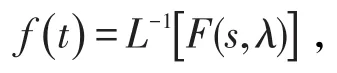
其中f(t)满足文〔1〕中性质1的条件。
证明:用假设法。假设存在两个满足文〔1〕中性质1的条件的不同函数f1(t),f2(t)都是函数F(s,λ)含参变量λ的拉普拉斯逆变换的原函数,即:

则,根据定义,有:

把上两式作差,利用含参变量的拉普拉斯变换的线性性质,得

性质2 (线性性质)若L[f1(t),λ]=F1(s,λ),L[f2(t),λ]=F2(s,λ),则

其中α,β是常数。
性质3(位移性质)若L[f(t),λ]=F(s,λ),则
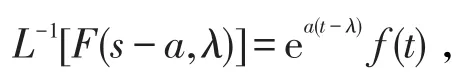
其中Res(s)>a。
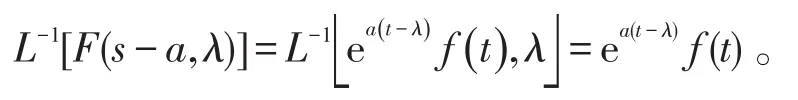
性质4(延迟性质)若L[f(t),λ]=F(s,λ),则

其中t>Res(a)。
性质5(积分性质)若L[f(t),λ]=F(s,λ),则
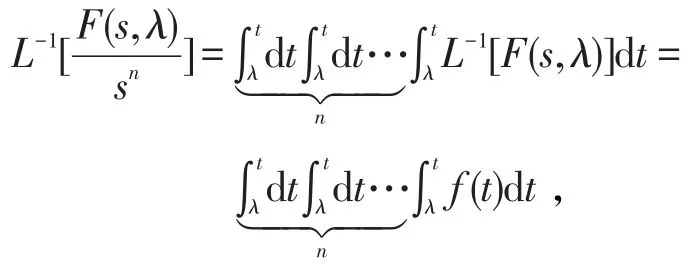
性质6 (象函数的微分性质)若L[f(t),λ]=F(s,λ),则

特别地,n=1时,L-1[F'(s,1)]=-tL-1[F(s,1)]。

性质8(卷积性质)若L[f(t)]=F(s,λ),L[g(t)]=G(s,λ),则
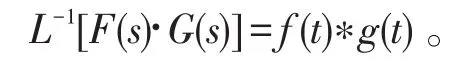
3 含参变量λ的拉普拉斯逆变换的应用
含参变量的拉普拉斯逆变换的计算,可以参照拉普拉斯变换〔5-12〕的计算方法。但要注意的是,在查表时,要根据参变量λ的值而定,题中给定参变量λ的值,在表中要取相应的参变量的值来分解象函数F(s,λ),从而求得原函数f(t)的表达式。
例1 求象函数

在参变量λ=1的原函数f(t)。
解:根据拉普拉斯逆变换性质,可得原函数为f(t)=δ(t)+2。
例2 求象函数

在参变量λ=-1的原函数f(t)。

所以,由位移性质,可得原函数为f(t)=t+te2t。
例3 求象函数

在参变量λ=-2的原函数f(t)。
从而可得原函数为f(t)=sin(-t)。
例4 求象函数

在参变量λ=α的原函数f(t)。
解:因为

根据线性性质,可得原函数为f(t)=t+1。
例5 求象函数
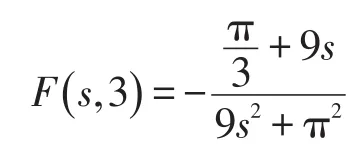
在参变量λ=3的原函数f(t)。

例6 求象函数

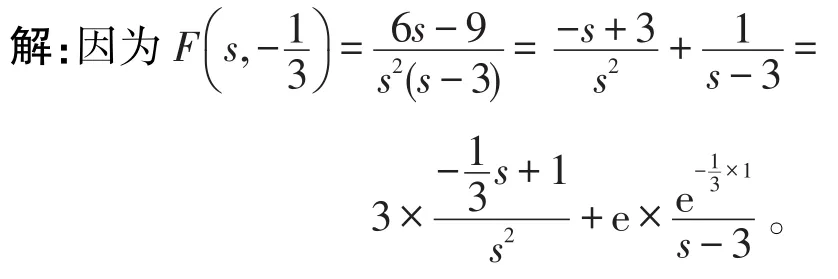
根据线性性质,可得原函数为f(t)=3t+e×e3t=3t+e3t+1。
〔1〕阳凌云,符云锦,邓光辉.含参变量的拉普拉斯变换及其应用〔J〕.湖南工业大学学报,2012,26(1):1-5.
〔2〕东北师范大学微分方程教研室.常微分方程〔M〕.2版.北京:高等教育出版社,2006:135-218.
〔3〕杨战民.复变函数与积分变换:题型·方法〔M〕.西安:西安电子科技大学出版社,2003:217-220.
〔4〕李建林.复变函数·积分变换:导教·导学·导考〔M〕.2版.西安:西北工业大学出版社,2003:276-278.
〔5〕张忠诚.拉普拉斯变换的应用研究〔J〕.周口师范学院学报,2006,23(2):40-42.
〔6〕张洁萍,李俊林.关于Laplace变换及其性质的应用研究〔J〕.太原科技大学学报,2011,32(3):249-251.
〔7〕ALAN V O,ALAN S W,NAWAB S H.信号与系统〔M〕.2版.刘树棠,译.北京:电子工业出版社,2013:417-441.
〔8〕刘明华,周晖杰.复变函数与积分变换〔M〕.杭州:浙江大学出版社,2012:189-210.
〔9〕冯卫兵.复变函数与积分变换〔M〕.徐州:中国矿业大学出版社,2013:188-213.
〔10〕张建国,李冱岸.复变函数与积分变换〔M〕.北京:机械工业出版社,2010:188-243.
〔11〕杜洪艳.复变函数与积分变换〔M〕.武汉:华中师范大学出版社,2012:142-162.
〔12〕姜立新.Laplace变换的应用研究〔J〕.枣庄学院学报,2010,27(2):37-40.

