灰色预测模型在高校非正常伤亡事件中的应用

韩同耀，何伟全，曾 慧，化存才*

（1.云南师范大学数学学院，昆明 650500；2.云南师范大学党委办公室，昆明 650500；3.云南师范大学教育科学与管理学院，昆明 650500）

非正常伤亡一般是指一些意外伤亡，即不是属于正常规律导致的伤害或死亡。随着教育部颁发大学扩招政策以来，内地大学招生规模不断地扩大，随之而来的是大学校园内发生非正常伤亡事件的数量不断上升。高校校园非正常伤亡事件的发生，不仅影响了大学生在校园里的正常生活与学习，而且还违背了建设和谐校园的宗旨，同时也成为高校网络舆情事件的重要诱因。因此，为降低校园非正常伤亡事件的数量，营造一个舒适的校园学习与生活环境，安全引导网络舆情，在本文中将基于数学中的灰色系统理论中的灰色模型GM（1，1）来建立针对校园非正常伤亡事件的预测模型。

灰色系统理论，是一种研究少数据、贫信息、不确定性问题的数学方法。灰色系统理论以“部分信息已知、部分信息未知”的“小样本”、“贫信息”的不确定性系统作为其研究对象，它主要通过对“部分”已知信息的生成、开发，并提取有价值的信息，实现对系统运行行为和演化规律的正确描述，并且能够进行有效的监控〔1〕。灰色预测就是利用灰色动态GM模型（Gray Model）对系统的行为特征量或者模型指标发展变化到未来一定时刻出现的数值进行预测〔2〕。

高校非正常伤亡是一个随机的事件，何时发生具有不确定性，促使其产生的因素也不尽相同。用灰色预测的方法分析高校非正常伤亡事件，其实质就是将高校非正常伤亡事件视为大学校园管理系统的灰色系统的灰色量，这里的灰色量是指大学校园管理系统中非正常伤亡事件的特征量。本文将利用云南某高校非正常伤亡事件的具体数据，通过累加，计算生成值，探究其内在的规律，参照灰色系统理论，建立起相应的模型来预测未来数据的变化趋势。

1 灰色预测建模方法

1.1 数据生成灰色系统建模中的数据生成：根据已有的数据资料，我们设

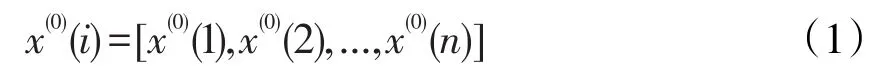
为系统输出的一组数据序列。

为了揭示系统的规律，灰色系统中采用独特的数据预处理，做一次累加得到x(1)(i)，消弱其随机性，得到有规律的生成值，即：

1.2 建立灰色GM（1，1）模型GM（1，1）模型是如下一阶单变量的灰色微分方程动态模型：

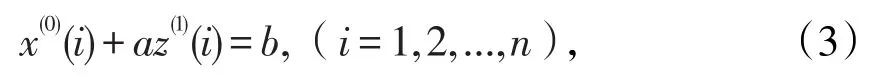
其中z(1)(i)为x(1)(i)的紧邻均值生成，即：z(1)(i)=0.5[x(1)(i)+x(1)(i-1)]，在灰色系统理论中，定义公式（3）的白化方程为：

其中a,b为常系数和模型的协调系数，它反应了数据间的变化关系。

协调系数可应用最小二乘法得到〔3〕：

其中，

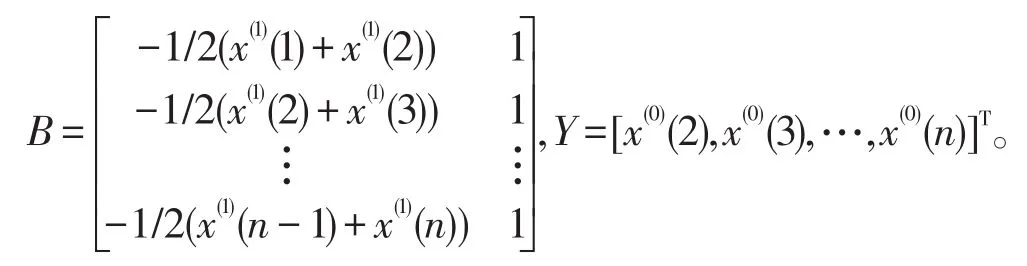
进一步可以解白化方程（4），得到：

对（2）和（6），可得到还原处理后的灰色预警模型为：

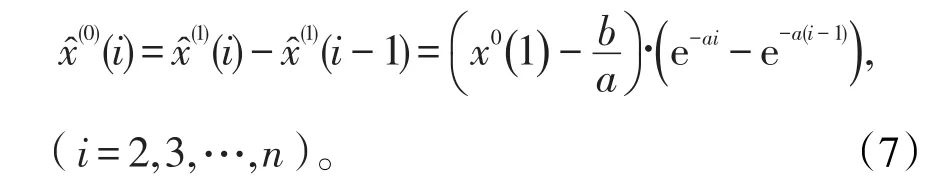
1.3 模型检验一般建立的模型都需要进行检验。我们将利用后检验法对GM（1，1）模型进行检验，确定所建立的灰色模型是否具有较高的精度，进而应用于预测实践中。

1.3.1 残差检验 绝对误差：

相对误差：

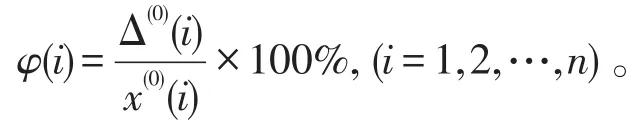
对于相对误差来说，只要φ(i)＜5%,就说明拟合值与预测值比较理想〔4-7〕。

1.3.2 后验差检验 由原始数据列x(0)(i)和灰色预测模型可给出它们的残差如下：

残差均值为：

原始数据列x(0)(i)的方差为：

残差的方差为：

后验差比值为〔5〕：

小误差概率为：

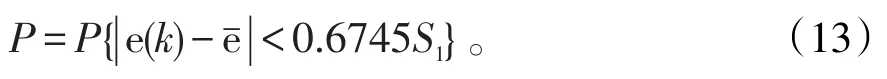
按照C与P值的大小，可将预测精度分为优、良、中、差4级，见表1〔6〕。

表1 预测精度等级表

若模型的预测误差较大或精度等级较差，则必须对灰色GM（1，1）模型进行如下修正:

②用均方根误差〔7-10〕

和平均相对误差

来提高精度。

2 模型应用实例

表2是云南某高校于2002至2012年之间发生的138起学生非正常伤亡事件的统计数据，本节中将依据此数据建立灰色预测GM（1，1）模型。

表2 学生伤亡事件次数

我们定义：大于10次的年份为校园非正常伤亡事件“加强防范年份”。对于这种年份，高校尤其需要特别警惕。根据表2中的实际数据，我们可对下一个“加强防范年份”做出预测（精度要求为2.0）。

2.1 计算原始数据列根据表2，我们得出要测量的原始数据列为：

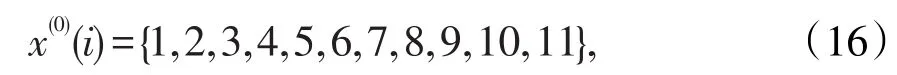
由前面的（2）式，经一次累加后得出：

2.2 参数计算根据（18）式，我们可以得出矩阵B，向量Y分别是：

即：a=-0.142440,b=2.832173。

2.3 建立灰色GM（1，1）模型把a=-0.142440,b=2.832173代入（6）式，得：

于是，通过上述计算，得出云南某高校的非正常伤亡事件的灰色预测GM（1，1）模型为：

表3 GM（1，1）分析结果

2.4 灰色GM（1，1）模型的精度检验

2.4.1 残差检验 如表3 所示，我们进行残差检验后，建立的GM（1，1）模型的相对误差小于0.5%，说明前面所建立的模型（19）精度较好。

2.4.2 均方根误差和平均相对误差检验 通过上述计算结果，由（14）、（15）式得：

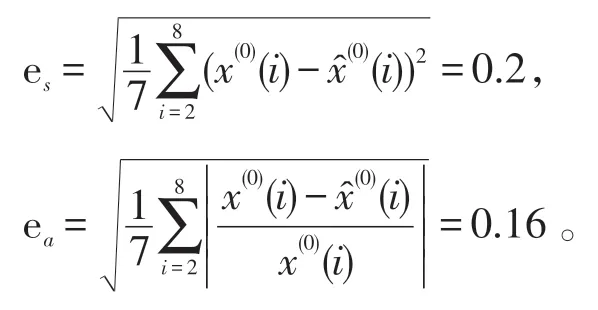
可以看出es和ea都小于给定的精度2.0，因此前面建立的灰色预测模型（19）可用，可以进行后期预测。2.4.3 后验差检验 采用后验差检验法对检验灰色GM（1，1）模型的精度，根据（8）-（13）式，可以分别得到：

按照表1 中关于灰色模型的预测精度的等级表，可以得出模型的预测精度为优，因而可用于外推预测。从所得预测值和原始值折线比较看出，预测结果较好，精度也较高，见图1。

图1 预测值与原始值对比

3 模型结果分析

4 高校加强非正常伤亡事件防范的措施

高校学生非正常伤亡事件的严重性不但影响到学生的生命健康、生活健康、经济损失等问题，而且也容易影响到学校正常的教学秩序，甚至于引发高校网络舆情，危及校园和社会稳定。因此，高校必须高度重视学生非正常伤亡事件的防范管理工作，建立高校学生非正常伤亡事件的“学校—保卫处—学院—班级—教师—家庭—学生”的预防及处理工作网络体系，确实维护高校校园的和谐稳定，为高校的建设与发展提供良好的环境保障。

4.1 强化高校安全法制教育，落实学校安全措施，提高学校相关部门防范水平，完善安全监管体系高校校级、各学院、各班级应坚持德育为首，加强学生法制教育及心理健康教育。首先，学校要把思想品德教育贯穿于整个学习和生活中。采用多层次分析评价体系，尊重并平等地对待每一个学生。其次，将安全法制教育纳入学校教学计划，大力宣传，以至于形成浓厚的法制教育氛围，以铲除校园伤亡事件产生的土壤。再次，因高校非正常伤亡事件的发生及校园安全环境与学生心理健康状况相关，故高校应做好到位的学生心理健康教育与咨询服务工作，如开展心理健康知识宣传，加强学生心理辅导工作，尤其是有严重心理问题的学生心理咨询及辅导工作。最后，加强校园安全工作的监查力度，加大校园周边环境有效整治的力度，为学校教育教学活动顺利开展、为师生健康生活营造一个平安和谐健康的外部环境〔11〕。

4.2 提高教师素质，营造和谐的校园环境良好师生关系是防止校园暴力的有效方式之一。一方面，要对教师进行心理健康教育，提高教师对自身心理素质的认识，促使教师自觉加强自身心理和行为的调适，自觉优化自己的心理和行为，为学生起表率作用。另一方面，学校管理者要努力为教师营造和谐的内在环境，主动为教师排忧解难，不断地改进领导方式，推行人性化的管理工作。同时，学校还应教育学生客观地评价教师，发展师生之间的正常交往，特别是拉近师生之间的心理距离，以缓解教师的心理压力，减少他们的挫折感，从而适时地抑制和减少高校非正常伤亡事件的发生〔12〕。

4.3 加强家校的合作与沟通工作，形成教育合力为防范高校学生非正常伤亡事件的发生，应当进一步加强和扩充教师之间、师生之间，特别是学校与家庭之间的沟通渠道。有组织、有目的地办好家长学校，定时间定内容，有针对性地对家长开展教育培训。通过家长会、座谈会、家教经验交流会等形式沟通联系，让家长了解学生在校情况，广泛听取家长的意见和建议，营造强大家校联动的安全教育合力。

总之，为维护学生、教职员工及高校的合法权益，保障高校正常教学秩序，维护校园和社会和谐稳定，高校应当做到以人为本，明确预防及处理范围，以公平、公正为目标，以规范预防和维护稳定为要求，建立合理的学生非正常伤亡事件的预防及处理工作网络体系。

〔1〕刘思峰，郭天榜，党耀国.灰色系统理论及其应用〔M〕.5版.北京：科学出版社，2002.

〔2〕傅立.灰色系统理论及其应用〔M〕.北京：科学技术文献出版社，1992.

〔3〕王宇熹，汪泓，肖峻.基于灰色GM（1，1）模型的上海城镇养老保险人口分析预测〔J〕. 系统工程理论与实践，2010，30（12）：2244-2253.

〔4〕易静，杜昌廷，王润华，等.应用灰色预测模型GM（1，1）对结核病发病率进行预测〔J〕. 重庆医科大学学报，2007，32（3）：275-278.

〔5〕沙爱敏，王晓东.基于灰色预测模型GM（1，1）的道路交通事故预测〔J〕.扬州职业大学学报，2007，11（1）:41-44.

〔6〕邓聚龙. 灰色控制系统〔M〕. 武汉：华中理工大学出版社，1985.

〔7〕化存才.数学建模应用与实践〔M〕.昆明：云南科技出版社，2008.

〔8〕杨华龙，刘金霞，郑斌.灰色预测GM（1，1）模型的改进及应用〔J〕.数学的实践与认识，2011，41（23）：39-45.

〔9〕任工昌.改进灰色模型在电力负荷中的预测分析及实现〔J〕.机械设计与制造，2010（2）:232-234.

〔10〕杨平.论灰色预测控制的应用条件和工作机理〔J〕.控制理论与应用，2011，30（5）:4-7.

〔11〕马宁奇.校园安全事故问责制的思考〔J〕.当代教育科学，2011（14）:48-49.

〔12〕张爽.近年来有关学校安全问题研究述略〔J〕.首都师范大学学报，2011（3）:51-60.