利用可加性求一类独立随机变量和的分布

王凡彬

（1.内江师范学院数学与信息科学学院，四川内江 641100；2.四川省高等学校数值仿真重点实验室，四川内江 641100）

设X和Y是两个独立的一维随机变量，如何求二者之和Z=X+Y的分布？目前有一些方法，也有较多讨论，得到了一些可应用的结果〔1-10〕。在连续随机变量的情形，常用的方法之一是应用卷积公式：

或

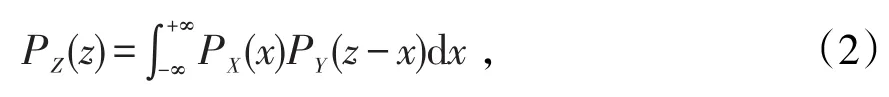
其中PZ(z),PX(x) ,PY(y)分别是Z, X, Y的密度函数。

不过，公式（1）、（2）在实际应用时，常常因为积分的繁难，而导致结果不易得到，或造成错误。

但是，我们还可利用某些随机变量具有的可加性，即“同一类分布的独立随机变量的分布仍属于此分布”，来求得Z=X+Y的分布。像正态分布，二项分布，泊松分布，Γ分布等，就具有可加性。在一些实际问题中，通过仔细观察，如果发现其随机变量是具有可加性的，就可应用可加性来解决问题，常可收到事半功倍的效果。

1 主要结果

下面我们主要通过一例来说明上述观点。

例 某种商品一周的需求量是一个随机变量，其密度函数为

设各周的需求量是相互独立的，试求①两周需求量的密度函数P2(x)；②三周需求量的密度函数P3(x)。

该例如果用卷积公式（1）或（2）是可以解决的，但是比较繁难。例如用公式（1），设Z2为两周的需求量，X1、X2分别是第一周、第二周的需求量，则Z2=X1+X2，

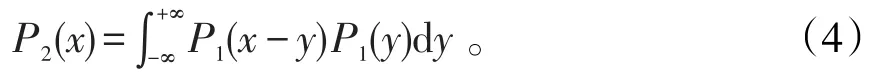
我们注意到（4）式只需在P1(x-y)P1(y)≠0的区域积分即可。但要满足这个条件，须x-y＞0，且y＞0，从而x＞y＞0，故

即

问题①得到解决。

再设Z3为三周的需求量，X3为第三周的需求量，则Z3=Z2+X3，

与前面类似，经过讨论，须在x＞y＞0时，P1(x-y)P2(y)≠0，故

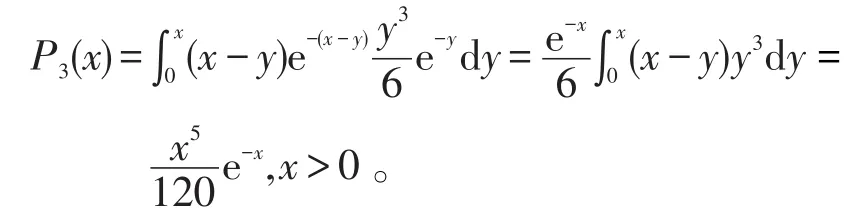
即

至此，问题②得到解决。

从上述过程来看，虽然解决了两个问题，但积分的过程有点繁难；且如果问题的周数换成较大的数字，如求100周的需求量的密度函数，或更一般的，求n周的需求量的密度函数，那用卷积公式（1）或（2）就很困难了，或许只有理论上的意义。

但是，如果利用可加性，本题或相类似的一些问题可能就变得容易了。考察Γ分布，其密度函数

仔细观察（3）式，发现实际一周的需求量X是服从参数为α=2,λ=1的Γ分布的，即X～Ga(2,1)。而我们知道，Γ分布是满足可加性的。即设随机变量X1，X2相互独立，X1～Ga(α1,λ), X2～Ga(α2,λ)，则

再看本例，设第i周的需求量为Xi，则Xi～Ga(2,1), i=1,2,…，且诸Xi间相互独立。问题①就是求Z2=X1+X2的密度函数，由（9），Z2～Ga(2+2,1)=Ga(4,1)，从而

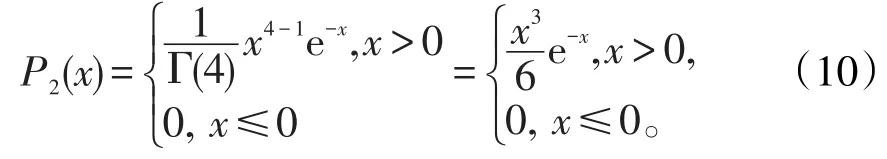
而问题②就是求Z3=X1+X2+X3的密度函数。由（9），Z3～Ga(2+2+2,1)=Ga(6,1)，从而

这样，由Γ分布的可加性，轻松解决了问题①和②。

2 结果的推广

实际上，本例的利用可加性的方法还可以推广。例如前面提到的，如要求前100周的需求量Z100的密度函数P100(x)，则Z100～Ga(100×2,1)=Ga(200,1)，

更一般的，前n周的需求量Zn～Ga(2n,1)，其密度函数Pn(x)为

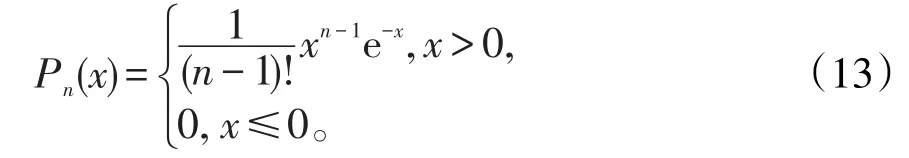
这都可以轻松得到结果，而上述结果用卷积公式操作起来相当麻烦，几乎是不可能完成的。

〔1〕茆诗松，程依明，濮晓龙.概率论与数理统计〔M〕.2版.北京：高等教育出版社，2013．

〔2〕王凡彬，严雳.多维随机变量函数密度的求解方法〔J〕.内江师范学院学报，2012，27（10）：17-19．

〔3〕王凡彬.多维随机变量函数变量变换法的推广〔J〕.井冈山大学学报：自然科学版，2013，34（3）：10-12．

〔4〕生志荣.二维连续型随机变量函数分布的一个定理〔J〕.高等数学研究，2011，14（4）：69-71．

〔5〕叶仁玉.关于连续型随机变量函数分布的探讨〔J〕.安庆师范学院学报：自然科学版，2010，16（4）：79-81.

〔6〕杨秀妮，王雪芹.随机变量函数的分布问题〔J〕.西安科技大学学报，2007，27（2）：316-319.

〔7〕马醒花，魏兰阁，彭宗勤.两个n维随机变量函数的概率密度的求法〔J〕.数学的实践与认识，2006，3（4）：174-177．

〔8〕李思齐，李昌兴，柳晓燕.二维连续型随机变量函数的分布密度的计算〔J〕.大学数学，2011，27（5）：162-166．

〔9〕宋明娟，王悦姣.二维随机变量函数的概率密度公式〔J〕.黑龙江科技学院学报，2011，21（5）：422-424．

〔10〕徐传胜，张敏.有关正态随机变量函数分布的探讨〔J〕．山东师范大学学报：自然科学版，2002，17（4）：91-93．