基于SIFT的全自动遥感图像配准算法

余 婷，厉小润

（浙江大学 电气工程学院，浙江 杭州 310027）

0 引 言

遥感图像配准是对两幅或多幅取自不同时间、不同传感器或者不同视角的遥感图像进行空间变换，通过寻优使输入图像与参考图像达到空间位置相匹配的过程［1］。通过图像配准可以对图像进行多源数据融合、目标变化检测、目标识别、图像镶嵌、时序图像分析等多种应用。

配准算法有四要素，分别为特征空间、搜索空间、搜索策略、相似性测度［2］。特征空间是指从参考图像和带配准图像中提取的用于匹配的特征集，如图像的灰度特征，几何特征如点、边缘、直线或者区域；搜索空间是指两幅图像之间建立的对应关系的所有可能变换集合，可以是两维的、三维的甚至是高维的；搜索策略是指在一个很大的搜索空间中寻找最优的变换模型参数，如果采用穷尽搜索的方法将需要很大的计算量，因此为减少计算量，必须采用相应的搜索策略，如Powell搜索策略；相似性度量是两幅图像是否匹配的尺度和标准，如本研究采用的互信息相似性测度。

现有的配准技术主要分为两大类：基于灰度的方法和基于特征的方法。基于灰度的方法直接利用图像的灰度信息来度量两图像之间的相似程度，它不需要对图像进行复杂的预处理，实现简单，但是对图像的灰度特性极其敏感，主要的算法有互相关法、序贯相似检测法、傅里叶变换法、互信息方法等［3］。基于特征的方法是从图像中提取一些几何特征，对它们进行匹配，最后得到一一对应的匹配控制点对。

本研究提出的全自动遥感图像的配准方法是结合了灰度信息和特征信息的复合式图像配准算法。首先，基于SIFT算子对输入图像进行粗匹配，确定初始变换模型参数；其次，在特征精匹配的过程中引入基于灰度的互信息算法，结合位置控制从而获得一一对应的控制点［4］；最后采用控制点结合加权最小二乘［5］的方法优化求解模型最优参数，对输入图像进行双线性插值显示图像。

1 算法描述

本研究提出的全自动配准算法是一种由粗到精的方法：粗匹配时采用SIFT特征匹配，将输入图像映射为一个具有平移、缩放、旋转不变性的局部特征向量集，通过两两比较找出匹配的若干对特征点对作为初始配准点；在此基础上再进行精细匹配，采用位置控制与互信息约束的方法，最后最优化求解最优模型参数。

1.1 基于SIFT特征的图像粗匹配

考虑到虚拟三角形的粗匹配对图像的尺度及畸变不具有鲁棒性，分辨率差异以及稍有畸变的图像配准误差较大，本研究采用SIFT特征进行粗匹配。SIFT特征是一种高维不变量信息描述子，它具有平移、缩放、旋转不变性。基于SIFT的遥感图像自动配准算法期望能够确定尽量多的、定位精确的且分布均匀合理的关键点，然后通过数据拟合来减少整体误差。

SIFT特征构造过程主要两个部分组成：关键点检测和不变量描述子构造。第1部分首先建立图像的多尺度空间，然后进行特征检测，获取一系列关键点以及它们的几何位置与尺度信息。第2部分通过联合关键点的多维信息来构造不变量描述子。本研究以关键点为中心建立一个区域，统计区域像素点的梯度直方图，寻找最大的峰值及它对应的方向，并以这个方向作为关键点的主方向。再联合区域的梯度信息建立多维特征向量，并对这个多维向量进行统一化，从而得到不变量描述子。

本研究参考文献［6－7］提供的方法，采用特征向量的欧氏距离作为相似性判定度量，计算最近邻（NN）和第二近邻（SNN）的距离之比（NN/SNN），把NN/SNN设定为最小阈值（本研究取0.3），如果SIFT描述子之间的欧式距离小于这个阈值，那么选择这些可靠性最高的匹配点作为初始配准点对来计算几何变换模型参数。

1.2 位置控制与互信息约束的特征精匹配

图像匹配的关键是定义一个有效的配准测度函数，并寻找空间变换关系，使变换后两幅图像的相似性达到最大，或者说差异性达到最小，保证两幅图像空间几何上的一致。

虽然不同光谱图像在灰度属性上存在较大差异，但是对同一地物、同一组织，其灰度分布又具有一定的相似性，因此研究者可以将图像像素作为随机变量，采用图像灰度分布的统计数据作为配准测度函数来实现图像配准。假设参考图像A的概率分布函数为PA(a)，浮动图像B的概率分布函数为PB(b)，图像A和B的联合概率分布函数为PAB(a,b)，则它们的互信息I(A,B)表示为：

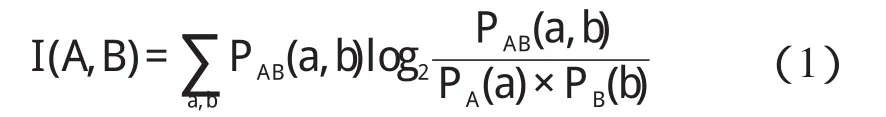
本研究在特征的精细匹配算法中采用位置控制结合互信息约束的方法实现，分别以两幅图像各个特征点为中心建立小区域，计算对应小区域的互信息值，以互信息为相似性测度［8］对提取到的更多特征点进行精细匹配。

假设在参考图像上提取到的角点集记为P={(xi,yi),i=1,2,...m}，在待配准图像上提取到的角点集记为Q={(xj,yj),j=1,2,...n}，取Q中的一点qk为例详细说明匹配的步骤：

（1）根据初始模型参数计算Q={(xj,yj),j=1,2,...n}中的点qk对应参考图像下的坐标，以这个坐标为中心点建立搜索窗，本研究设定区域大小为10×10（可以根据图像大小变化）。把点集P={(xi,yi),i=1,2,...m}中落在搜索窗内的点作为qk的候补对应点。

（2）在待配准图像上以候补对应点为中心，选取一小块区域ar e a1，本研究设定区域大小为4×4，按分辨率差异比例在参考图像上选取ar e a2，之后将其插值到与ar e a1大小分辨率相同。

（3）求取两块小区域的互信息。

（4）每个qk的候补对应点都进行步骤（2）和步骤（3），取互信息最大的那个特征点作为筛选后和qk对应的控制点。

通过以上4个步骤，笔者对提取到的特征进行了再次匹配，获得位置控制与互信息约束的控制点对。

1.3 最优化求解最优模型参数

最优化求解［9］是一个不容忽视的步骤，它是指求取参考图像和待配准图像之间最佳模型参数的过程。现有的图像配准方法中常用的算法有图匹配算法、Powell方法、Downhill simplex方法［10］等。本研究采用的是控制点结合加权最小二乘准则算法，这是一种比较通用的变换模型参数估计办法。

假设：

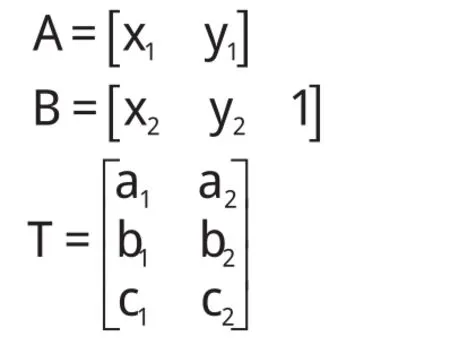
则变换式表示成：

A=B×T

在最小二乘的算法求解过程中，笔者认为不同误差精度的控制点对对模型参数求解结果的影响不一样，参考图像中的点与待配准图像经过变换后的点之间的误差越大，则它们对最后参数求解的影响越小，因此本研究引入一个加权矩阵［11］。

本研究用ex()i表示第i对控制点在x方向的误差，用ey()i表示第i对控制点在y方向的误差，则误差距离表示为：

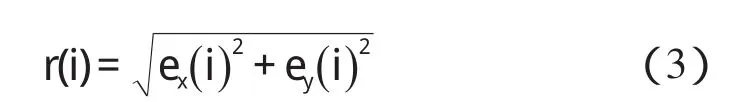
加权矩阵由r(i)构成，表示为：

其中：

利用加权最小二乘法使平方误差式（6）最小，由此获得最优模型参数。

2 实验的仿真

本研究选用的参考图像是高光谱图像的一个波段图，图像大小为550×360（单位：像素，下同），待配准图像是经过ENVI软件的裁剪旋转尺度变换过的图，图像大小为545×38 3。已知仿射变换的模型参数值，笔者分别对以下3种算法进行仿真：实验1是文献［1］配准算法仿真，记为LAB1；实验2是文献［9］配准算法仿真，记为LAB2；实验3是本研究提出的由粗到细的配准算法仿真，记为LAB3；本研究把以上3个实验分为两组进行分析比较。

传统课堂教学的最大特点,是以教师为主体,向学生灌输知识,学生处在被动地位。特别对于“纳米材料”这种新兴学科,涉及到的基础学科多,知识更新快,又是全英文教学,传统的灌输模式使学生能够理解的内容有限,且对教师的知识储备和体力精力都有很高的要求,而且学生在进行课程学习的同时往往已经进入实验室具体科研课题研究的阶段,必然会存在应用课堂知识的具体问题。因此在教学模式上,力求让学生占据主动地位,以学生为课堂主体,加强教师和学生之间的交流[8]。

图1 参考图（左）及待配准图（右）

图2 LAB1获得的匹配控制点图

图3 LAB2获得的匹配控制点图

图4 LAB3获得的匹配控制点图

两幅原始图像如图1所示。LAB1、LAB2、LAB3最终取得的控制点图如图2～4所示。配准结果图如图5所示。

3 评价标准

图5 LAB1、LAB2、LAB3的配准结果图（从左到右）

图6 LAB1、LAB2、LAB3的配准镶嵌图（从左到右）

图7 配准精度直方图

本研究采用3种评价标准来对配准精度的进行评价，它们分别是均方根误差、镶嵌图以及联合直方图。均方根误差以及镶嵌图是现有的常用的评价标准，联合直方图评价则是本研究的又一创新点。

3.1 均方根误差评价

已知实际的模型变换参数，变换模型表达式为：

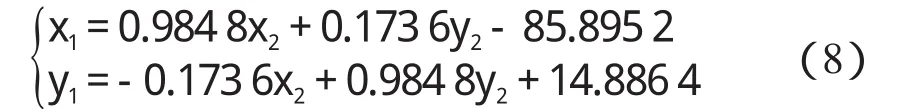
将均方根误差作为配准精度的评价标准。均方根误差表示为：

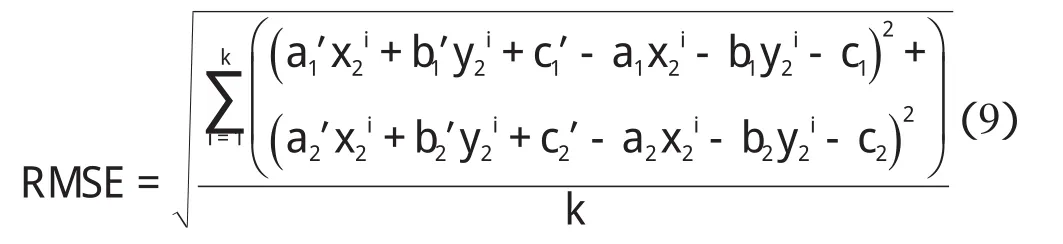
式中：a1′，b1′，c1′，a2′，b2′，c2′—模型参数的实际值；a1，b1，c1，a2，b2，c2—经算法仿真求得的模型参数值；k—算法得到的控制点对的个数。

统计3个实验数据得到结果如表1所示。

从表1中可以看出LAB3的模型参数值最接近真实值，且均方根误差最小，因此可知本研究算法具有更高的配准精度。

3.2 镶嵌图评价

由于均方根误差的评价标准比较抽象，为了更直观形象的评价，现有的很多应用都采用镶嵌图［12］作为评价标准。本研究中3个实验结果的镶嵌图如图6所示。

由图6很难比较出哪个实验具有更高的配准精度，因此本研究引入联合直方图，以比较3组图像的配准精度。

3.3 联合直方图评价

两幅图像的联合直方图是通过统计两幅图像的对应位置的灰度对(i,j)出现的次数而得到的。本研究中用二维图形表示：X轴表示参考图像的灰度极值，Y轴表示带配准图像灰度极值，当两幅图像完全一样时，图形的所有点都分布在一条斜率为1的直线上，随着两幅图像相似度的降低，图形的点将分散分布在对角线周边。

考虑到参考图像和待配准图像包含的地域并不完全相同，全局图像输入得到的直方图并不准确，本研究从两幅图像共同的区域中提取出大小160×160的区域作为联合直方图的输入，观察图像中的点是否逼近斜率为1的对角线。

实验1、2、3的配准精度直方图如图7所示。由图7可知，LAB3的直方图的点比较集中的分布在对角线周边，而LAB1、LAB2的点相对来说比较分散，因此LAB3中两幅图像相似度最高，具有更高的配准精度。

表1 LAB1、LAB2、LAB3仿真得到的模型参数值及均方根误差

4 结束语

本研究提出的这种基于特征的由粗到细的全自动配准算法是基于SIFT特征粗匹配和位置控制互信息约束进行特征精匹配的全自动遥感图像配准算法。首先采用SIFT特征匹配，将输入图像映射为一个具有平移、缩放、旋转不变性的局部特征向量集，采用特征向量的欧氏距离作为相似性判定度量，通过两两比较找出匹配的若干对特征点对作为初始配准点，对输入图像进行粗匹配。然后引入互信息，以互信息为相似性测度，在位置控制的搜索策略下进行特征精匹配，优化模型参数。通过仿真和数据，验证了本研究算法在图像配准上的有效性。

与传统的基于虚拟三角形角点特征自动配准算法相比，本研究算法在后续进行了互信息位置控制的精细配准，显然配准精度更高；其次，本研究的算法也优于一般的由粗到细的配准算法，基于SIFT方法提取的特征对图像具有尺度不变性，对图像畸变也有更高的鲁棒性，LAB2的特征粗匹配的过程中，若待配准图像发生了纵横方向的特殊畸变，则对应匹配的三角形的各个角的比就不近似相等，此时，研究者就应该采用本研究的对图像尺度变化以及图像畸变具有更高的鲁棒性的SIFT匹配算法。综上所述，本研究基于SIFT的由粗到细的配准算法显得更加具有优越性。

（

）：

［1］吕金建，文贡坚，李德仁，等.一种基于虚拟三角形的图像自动配准方法［J］.信号处理，2008，24（5）：737－741.

［2］吕金建，文贡坚，李德仁，等.一种基于角点特征的图像配准方法［J］.遥感技术与应用，2007，22（3）：438－442.

［3］吕金健.基于特征的多源遥感图像配准技术研究［D］.长沙：国防科技大学电子科学与工程学院，2008.

［4］董博宇.多源遥感图像配准技术研究［D］.哈尔滨：哈尔滨工业大学，2009.

［5］王 伟，苏志勋.基于移动最小二乘法的医学图像配准［J］.计算机科学，2010，37（9）：270－271.

［6］程 焱，周 焰，林洪涛，等.基于SIFT特征遥感影像自动配准与拼接［J］.遥感技术与应用，2008，23（6）：721－728.

［7］DAVID G.Lowe distinctive image features from scale－invariant key points［J］.International Journal of Computer Vision，2004，60（2）：91－110.

［8］YU Ting，LI Xiao－run.Remote Sensing Image Registration Based on VTS－PCMIC Algorithm［C］.Fuzzy Systems and Knowledge Discovery（FSKD），2012 9th International Conference，2012：48－52.

［9］DARE P，DOWMAN I.An improved model for automatic feature－based registration of SAR and SPOT images［J］.ISPRS Journal of Photogrammetry&Remote Sensing，2001，56（1）：13－28.

［10］MIKOLAJCAYK K，SHHMID C.Scale＆affine invariant interest point detectors［J］.International Journal of Computer Vision，2004，60（1）：63－86.

［11］LI W，LEUNG H.A maximum likelihood approach for image registration using control point and intensity［J］.IEEE Transactionson ImageProcessing，2004，13（8）：1115－1127.

［12］GOSHTASBY A，STOCKMAN G.Point pattern matching using convex hull edges［J］.IEEE Transactions on Systems，Man and Cybernetics，1985，15（4）：631－637.