基于暂态量主频特征的高压线路继电保护研究*

高效海，张雪松，张 波，王慧芳，何奔腾*

（1.浙江大学 电气工程学院，浙江 杭州 310027； 2.浙江省电力试验研究院，浙江 杭州 310014）

0 引 言

超高压输电线路的暂态保护是继电保护领域中的一个重要研究方向[1-4]。它能实现迅速切除故障，加快线路恢复供电，提高系统稳定性。目前，已有很多利用暂态故障分量信息构成的继电保护方法[5-8]。如文献[9-10]利用双端暂态量构成差动保护，这种保护方式可靠性高，但成本较高，且依赖于两端时间同步和传输通道。文献[11]利用单端行波构成距离保护，文献[12]提出边界保护，这些保护不依赖于传输通道和时钟同步设备，但可靠性还难以确定。文献[13-14]提出了基于固有频率的保护和测距方式，但受线路两端折射系数和反射系数的影响。

通过对超高压线路暂态过程的分析，笔者所在实验室提出了超高压线路暂态过程估算方法，并通过合理简化，确定了各暂态主频率与故障距离的关系。本研究进一步从理论上探讨利用该关系构成继电保护的可行性。首先在故障线路暂态特征分析的基础上提出“通过提取某一暂态主频率的值，计算出故障距离，构成单端暂态保护”的方法；然后分析影响保护可靠性的各种因素，并给出减少这些因素影响的方法；最后通过仿真验证理论的正确性。

1 故障线路暂态特征分析

根据文献[4]，发生故障的电力系统如图1所示。电力系统相对应的故障分量系统的等效图如图2所示[15-16]。

图1 故障系统图

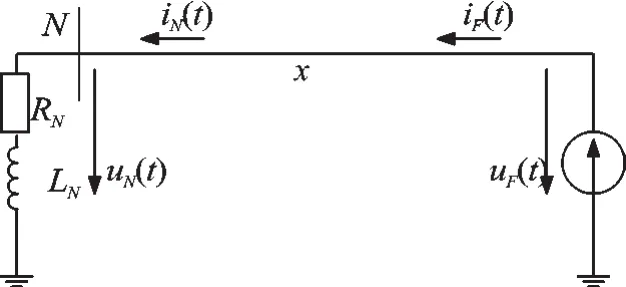
图2 故障分量系统

根据文献[4]，得到暂态频率与系统及线路参数间的关系，如下式：

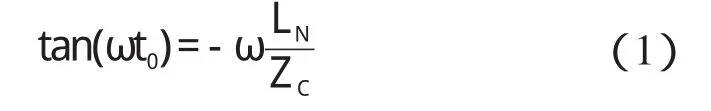
式中：t0=x/v，v—行波传播速度,ZC—线路波阻抗，ω—暂态频率。

式（1）表明，当故障距离和系统及线路参数一定时，该特征方程有无穷多个根，记做ωm,m=1,2,…。每个根可以等效地看成正切曲线与一条直线的交点。在频域内，则表现出一系列频率的形式，本研究称之为暂态主频率。当故障距离变化时，这些暂态主频率都会随之改变。文献[4]给出了各暂态主频率分量下，电流幅值的大小为：

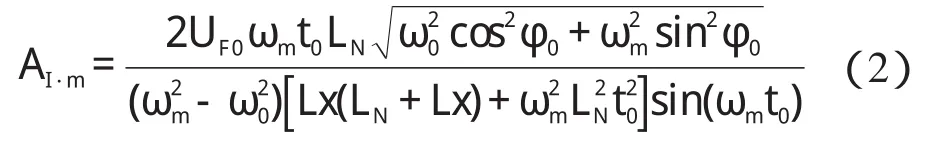
式中：AI·m—电流在ωm频率分量下的幅值大小。

式（2）表明：暂态主频率ωm对应的次数m越大，时域内相应频率的电流幅值AI·m越小。在这一系列暂态主频率中，正切曲线与直线的第一个交点ω1称之为一次主频，它是除了工频以外，时域幅值最大而频率最小的暂态主频率。除一次主频率外还有其他暂态主频率分量，按这些暂态主频率由小依次变大的顺序，分别称之为二次主频、三次主频等。

电流幅频特性如图3所示。

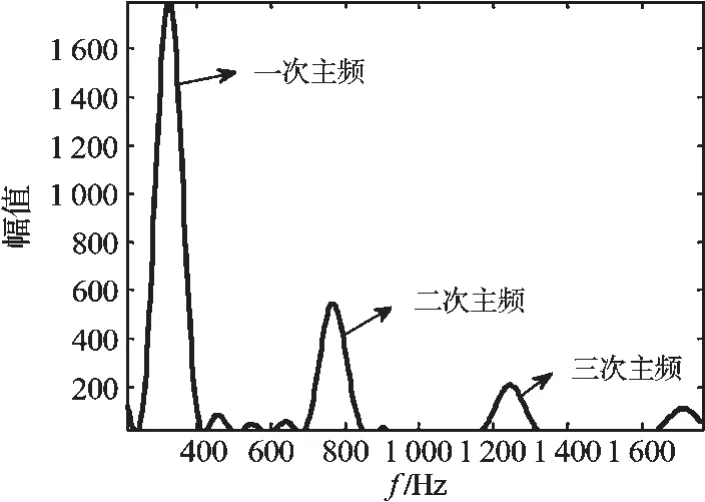
图3 电流幅频特性

当故障距离变化时，各次暂态主频率的大小也随之变化。将t0=x/υ代入式（1），求出m次暂态主频率ωm和故障距离x的关系：

式中：α=-LN/ZC；m—暂态主频率的次数，一次主频时，m=1，二次频时，m=2，三次频时，m=3，以此类推。

各次主频和故障距离x的关系图如图4所示。

图4 故障距离和各次主频的关系

根据公式（3）和图4可知，故障距离和系统电流各暂态主频率值有特定关系。故障距离越大，系统暂态电流各次暂态主频率值就越小。研究者通过提取某次暂态主频率分量，按式（3）可计算出故障距离。由此可以实现基于电流暂态特征的继电保护。

2 保护方案

2.1 测距误差分析

为掌握频率测量误差与故障距离误差间的关系，对式（3）求导，可得：

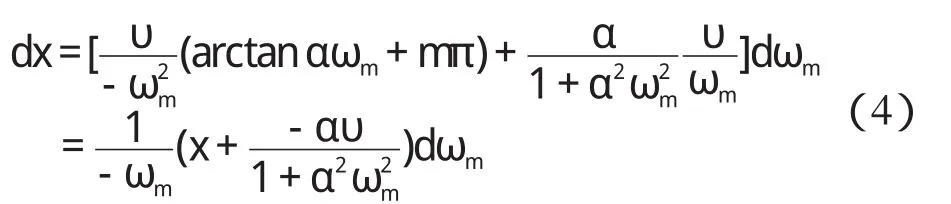
若频率测量绝对误差为Δωm，且Δωm很小，根据式（4），可近似求得测距绝对误差Δx，即：

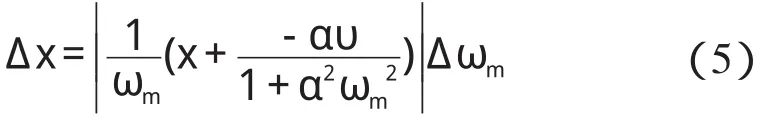
因为α=-LN/ZC，-αυ为正数。式（5）表明：

（1）相同频率测量误差Δωm下，随着故障距离的增加，一方面暂态主频率ωm减小，另一方面x增大，故测距误差Δx增大。

（2）相同故障距离x下，暂态分量中的主频率次数越大，对应的频率值越大，相同测量频率误差下，测距误差越小。

因此，故障距离的测量误差与频率提取的精度、故障距离和选择暂态主频率次数的大小有关。频率提取误差越小、故障距离越短、暂态主频率次数越大，故障距离测量误差越小。

为减少测距误差，提高保护的可靠性，可以从以下两方面进行研究：

（1）提高频率的提取精度。传统的频率提取方法为傅立叶变换，提取精度与采样频率和数据长度有关。由于保护时限和保护硬件的要求，研究者通过傅立叶方法提高频率测量精度有限。但可以通过优化数据，消除工频影响来提高提取精度。

（2）选取适当的主频率次数。由式（1）可知，电流暂态主频分量按照暂态主频率从小到大，依次为一次主频、二次主频、三次主频等。每一个暂态主频率和故障距离都存在式（3）的关系，通过提取任一暂态主频率的大小，都可以计算故障距离。本研究为了减少误差，相同故障距离下，希望选择的暂态主频率次数越大越好。但是暂态主频率次数越大，其对应时域幅值越小，提取越困难。综上考虑，不同故障距离时，通过选取适当的主频率次数会提高测量精度。

2.2 数据优化

在傅里叶变换基础上，本研究利用二次积分消除工频分量影响的方法来优化数据，使主频率的提取精度提高。

故障线路的短路电流中除包含直流分量、工频分量外，还包含一系列暂态主频率分量，如下式所示：

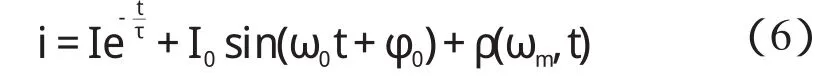
式中：—衰减的直流分量，τ—直流衰减常数，I0s i n(ω0t+φ0)—工频分量，ρ(ωm,t)—其他各暂态主频率分量。

其中工频分量最大，对式（6）进行积分得：

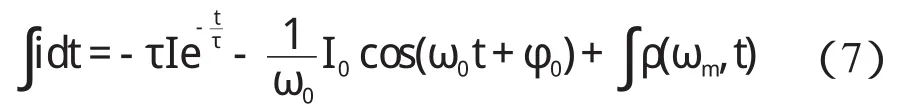
对式（7）再次积分，可以得到：

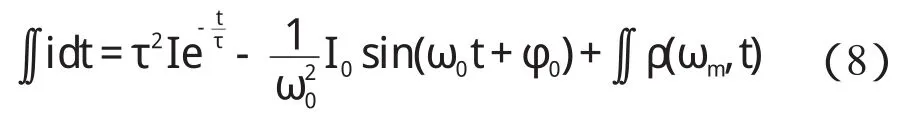
将式（8）除以ω20，然后将其结果与式（6）相加，并消去工频分量，可整理得：

通过上述变换，式（9）消去了工频分量，使得其他各暂态主频率分量的幅频特性更明显。

本研究设i(n)为电流采样值序列，是一个有限时间的序列。式（6～9）可以表示成以下迭代方式：

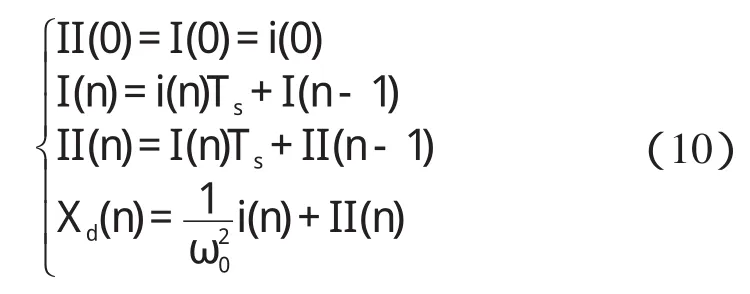
式中：i(n)—采样序列，I(n)—i(n)积分一次的序列，II(n)—i(n)积分两次的序列，Ts—采样周期，Xd(n)—最终除去工频影响的序列。

对式（10）中的Xd(n)求导，以减少序列中直流分量，得：

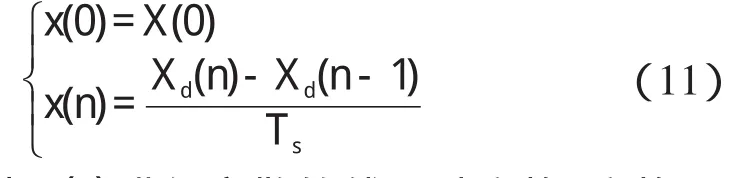
对式（11）中x(n)进行离散的傅里叶变换，变换公式为：

式中：N—数据长度

其对应的幅频特性为：

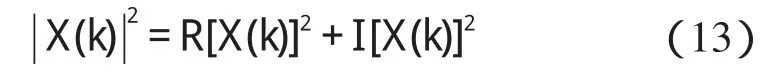
在2π范围内，式（13）包含了各次频率的幅值信息，k点的频率实际为：

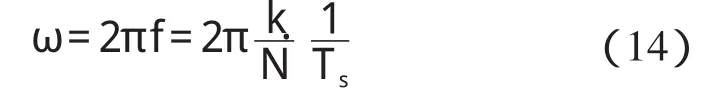
因此根据幅频特性，幅值最大的频率为一次主频ω1，其次为二次主频ω2，依次类推，ωm均可求出。

2.3 保护方案

保护方案如图5所示。

故障距离测量的准确度直接影响保护的正确动作。为此本研究在后续的仿真中只对故障测距结果进行分析，然后探讨这种保护方案的可行性。

3 ATP算例仿真

3.1 仿真系统与参数

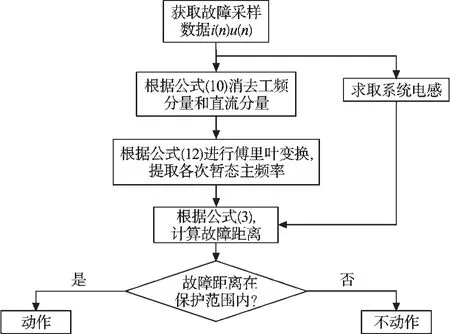
图5 保护方案流程图

本研究采用实际线路典型参数对故障的暂态特性进行分析，利用ATP进行仿真，按照上述傅里叶变换法提取暂态主频率的大小并计算故障距离。

系统的仿真模型如图6所示。

图6 EMPT仿真图

500 kV系统典型参数如表1所示。

表1 各元件及仿真参数

3.2 距离测量仿真结果

仿真中采用三次主频率。本研究设故障距离分别为100 km、300 km和500 km，在不同系统阻抗情况下利用傅里叶变换提取3次暂态主频率，计算而得的故障距离结果如表2～4所示。

从以上仿真结果可以看出，在采样时间为5 ms时，尽管傅里叶变换法提取暂态主频率本身存在一定误差，故障距离测量相对误差仍不超过3%，可见，本研究所提出的利用故障电流暂态特征分量构成保护的方案是可行的。

另一方面，从仿真中可以看出，故障距离越远，三次暂态主频率越小，利用傅里叶变换法测量三次主频误差也就越大。本研究通过提取三次暂态主频率，利用式（3）得出测量距离，其误差也随着故障距离的增大而增加。这与理论分析结果相符合。

以上结果分析同样适用于利用提取其他次暂态主频率来计算故障距离的情况和三相系统故障。

对于实际线路，虽然分布参数是一个随频率变化的量。但线模分量的线路参数随频率变化不大，故利用线模分量参数可以减少因线路参数不理想带来的误差。

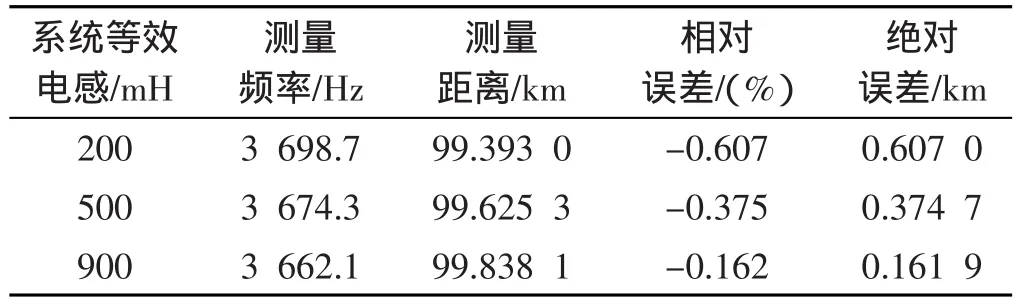
表2 故障距离为100 km时仿真结果

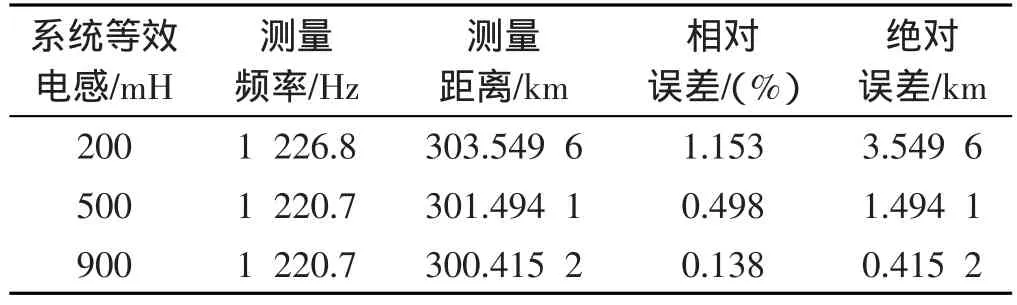
表3 故障距离为300 km时仿真结果

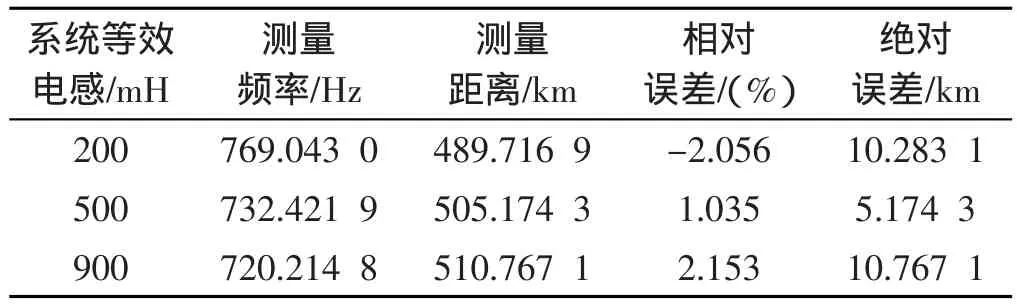
表4 故障距离为500 km时仿真结果

4 结束语

本研究从理论上探讨了利用暂态主频率构成单端暂态保护的可行性，分析了影响测距误差的因素，指出暂态主频率提取的误差、故障距离和选择暂态主频率次数的大小都影响着故障距离测量的误差，并给出了减少误差的方案。理论研究和仿真分析表明，暂态主频率提取误差越小、故障距离越短、暂态主频率次数越大，故障距离测量误差越小。

由此可见，频率提取的精度和快速直接影响继电保护的可靠性。如何快速、精确地提取暂态频率，值得接下来进行进一步研究。目前，该保护方案可以作为辅助措施，提高继电保护的可靠性。

（References）：

[1] 葛耀中.新型继电保护与故障测距原理与技术[M].西安：西安交通大学出版社，2007.

[2] 朱声石.高压电网继电保护原理与技术[M].北京：中国电力出版社，2005.

[3] 胡广书.数字信号处理—理论算法与实现[M].北京：清华大学出版社，1997.

[4] 张 波，何奔腾.特高压输电线路暂态特征估算方法[J].电力自动化设备，2010，30（5）：1-5.

[5] 翁舟波，田 羽，范春菊，等.带同杆双回线的T型支接线的故障测距的研究[J].继电器，2007，35（13）：6-10.

[6] 胡 巨，杨明玉.利用暂态电流的高压输电线路暂态保护新方案[J].继电器，2005，33（1）：21-23.

[7] 李晓珂，李详发.配电网合环冲击电流的暂态过程分析与仿真[J].机电工程，2010，27（5）：67-70.

[8] 段建东，张保会，周 艺，等.超高压输电线路单端暂态量保护元件的频率特性分析[J].中国电机工程学报，2007，27（1）：37-43.

[9] 罗四倍，段建东.基于暂态量的EHV/UHV输电线路超高速保护研究现状与展望[J].电网技术，2006，30（22）：32-41.

[10] 卜春霞，张义含，姜自强，等.超高压线路暂态保护选相研究[J].电力系统保护与控制，2010，38（16）：30-34.

[11] 陈 平，葛耀中，徐丙垠，等.现代行波故障测距原理及其在实测故障分析中的应用—A型原理[J].继电器，2004，32（2）：13-18.

[12] 哈恒旭，张保会，吕志来.边界保护的理论基础第一部分-故障暂态分析[J].继电器，2002，30（9）：7-10.

[13] 黄少锋，王兴国，刘千宽.一种基于固有频率的长距离输电线路保护方案[J].电力系统自动化，2008，32（8）：59-63.

[14] 邬林勇，何正友，钱清泉.单端行波故障测距的频域方法[J].中国电机工程学报，2008，28（25）：99-104.

[15] 孙 琳.输电线路中潜供电流的电路分析和计算[J].机电工程技术，2011，40（5）：21-23.

[16] 索南加乐，齐 军，陈福锋，等.基于R-L模型参数辨识的输电线路准确故障测距算法[J].中国电机工程学报，2004，24（12）：123-129.