基于优化的GRNN和BP神经网络的磁滞曲线拟合对比分析*

何汉林，孟爱华*，祝甲明，宋红晓

（1.杭州电子科技大学 机械工程学院，浙江 杭州 310018；2.杭州浙大精益机电技术工程有限公司，浙江 杭州 310000）

0 引 言

由于GMM具有输出力大、机电耦合系数大、能量密度高、响应速度快和应用频率宽等优点，使得在精密驱动技术中，GMM的应用非常广泛。但是，由于磁性材料的磁滞非线性，使得由GMM制成的超磁致伸缩执行器（GMA）的输入和输出存在着一定的滞后，给GMA的精确控制带来了一定困难。因此，怎样去拟合磁滞环已成为各国学者研究的热点。目前，国际上通用的磁滞模型主要有3种：一种是基于数学的唯像模型，典型代表为Preisach模型；一种是基于材料内部机理的物理模型，典型代表为J-A模型；还有一种是基于自由能和统计学分布理论的自由能磁滞模型。其中，运用preisach模型时，需要测出大量的一阶折返曲线，但是折返曲线的测量非常繁琐，对实验器材的精度要求也比较高，工作量庞大；运用J-A模型来反映GMM磁滞特性时，需要辨识和调整大量的物理参数；自由能磁滞模型兼顾了Preisach模型和J-A模型的部分优点，但是该模型的运算量很大，而且没有考虑涡流损失的影响[1]。除此之外，最近几年新兴起来的还有神经网络模型。神经网络模型中最常用的为误差逆向传播的前馈BP网络，理论证明，BP网络可以以任何给定的精度去拟合强非线性的连续函数或者映射关系，不过BP算法的误差曲面上存在高频分量，而且存在局部极小问题[2-6]。而径向基网络无论是在逼近能力、分类能力还是在学习速度等方面均优于BP网络。李贵存等[7]用混合径向基函数网络去拟合磁滞曲线，有效克服了BP神经网络和径向基函数神经网络在拟合磁滞回线各方面的缺点，效果比较理想。不过该方法程序复杂，而且径向基函数的扩展系数采用默认值，并不是最佳值。

在此，笔者提出一种基于径向基网络的变化形式—广义回归神经网络（GRNN）去拟合磁滞非线性，并对传统的GRNN神经网络进行优化，利用交叉验证方法训练神经网络，使得训练后的样本值能够更好地预测输出；同时，采用循环算法找出最佳的径向基函数的扩展系数，以构建最佳的GRNN网络，并与BP网络拟合进行对比分析。

1 GRNN神经网络非线性逼近

1.1 GRNN神经网络的理论基础

GRNN的理论基础主要是非线性回归，计算非独立输出变量Y相对于独立的输入变量X的非线性回归，主要是得出概率最大的y。设f(x,y)为随机变量x和随机变量y的联合概率密度函数，X为x的观测值，则条件均值为[8]：

式中：X—输入，Y—输出，—Y的预测输出。

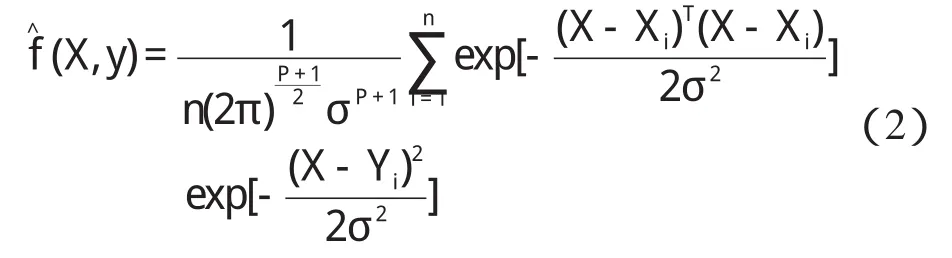
式中：n—样本容量；Xi，Yi—随机变量x和y的样本观测值；p—随机变量x的维数；σ—光滑因子。

如果用估算密度函数去代替f(X,y)，代入式（2）中并交换积分次序，则上式变为：

样本Xi与X之间Euclid距离平方的指数即为相应的观测值Yi的权重因子，估计值Y∧(X)为所有的Yi的加权平均。当光滑因子σ比较大的时候，估计值Y∧(X)近似为所有样本值的均值；当σ趋向于0时，Y∧(X)近似为训练样本，这时，如果被预测点包含在训练样本中，则预测值会和样本中的值非常接近，如果被预测点不包含在训练样本中，则预测误差可能会比较大。只有当σ取值适中时，所有的训练样本才都被考虑进去。

当用GRNN网络拟合磁场强度和GMM应变曲线时，以磁场强度作为自变量，则GMM的应变ε关于磁场强度H的预测输出为：

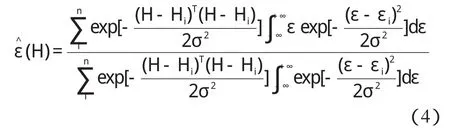
利用该公式，根据输入磁场强度样本H，便能得到GMM应变ε的预期输出。

1.2 基于GRNN神经网络的磁滞曲线拟合

GRNN为3层神经网络，第2层为径向基隐层，输出层为一个特殊的线形层。其结构如图1所示。

图1 GRNN网络结构

其中：

式中：P—输入，W—权重，b1—阈值，R—输入向量元素的数目，Q—输入目标样本数目。

在GRNN神经网络中，阈值b1=0.832 6/SPREAD，第1层神经元的网络输入即为加权输入与相应阈值的乘积，然后通过式（5）计算就可以得到第1层神经元的网络输出。从上面计算阈值的公式中，可以看出径向基函数的扩展系数SPREAD值对网络的阈值有很大影响，而阈值对网络的性能又有很大影响。通常情况下GRNN网络中SPREAD值的选用原则为使得第1层输入向量与神经元权值向量之间的距离为0.5，该距离可以通过Mtalab中dist函数计算得到，默认值为1.0。不过1.0只是一个经验值，在该SPREAD值下，网络的预测误差未必最小。为了提高网络的预测精度，设置合理的SPREAD值是关键。同时，由于所取的训练数据较少，为了扩大样本容量，笔者采用交叉验证方法来训练GRNN神经网络，并用循环方法找出最佳的SPREAD值和输入、输出，在该条件下构建最佳GRNN神经网络。为了便于观察神经网络的预测效果，本研究将网络预测的曲线与J-A模型仿真曲线进行了对比。对比所用的J-A模型曲线来自于Calkins和Smith所建[9-11]，该模型的工作条件为：偏置磁场为0 kA/m，频率为1 Hz，负载等效刚度系数Kl为5.67×105N/m。

由于神经网络只能逼近任意单值映射函数，而磁滞曲线是非线性多值映射关系，本研究中将磁滞曲线分为外加磁场强度增加阶段和磁场强度减小阶段两部分，分别用神经网络去逼近，再把两部分合在一起。为了便于分析BP网络和GRNN网络的拟合效果，笔者分别用BP网络和GRNN网络去拟合磁滞曲线。

实验方案设计如下：从Calkins实验曲线上磁场强度增加的那一部分随机的取得47组数据作为网络的训练数据，随机的取得46组数据作为网络的预测数据。从实验曲线上磁场强度减小的那一部分随机的取得47组数据作为训练数据，再随机地取47组数据作为预测数据。采用Matlab中crossvalind函数来交叉验证训练神经网络，SPREAD最佳值从0.1～2之间循环求解，可得最佳SPREAD值为0.1。

程序工作流程图如图2所示。

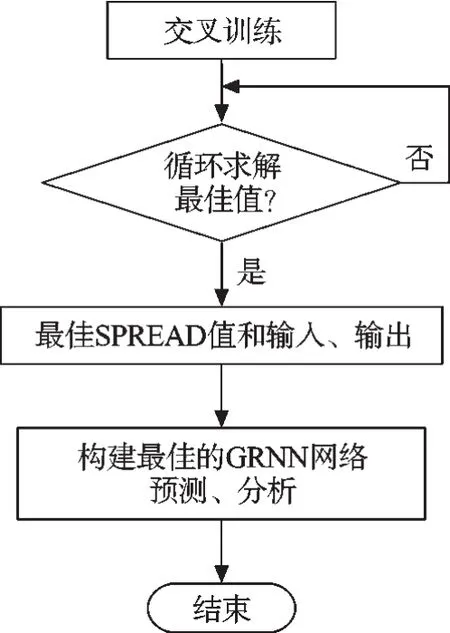
图2 程序工作流程图

在此扩展系数下的网络预测如图3～图6所示。

图3 磁场强度增加阶段GRNN神经网络预测输出

图4 磁场强度增加阶段GRNN神经网络预测误差

图5 磁场强度减小阶段GRNN神经网络预测输出

图6 磁场强度减小阶段GRNN神经网络预测误差

从图3～6中可以看出，相对于J-A模型理论曲线来说，GRNN神经网络的预测输出曲线和实验的实际输出曲线还是比较接近的，磁场强度增加阶段的网络预测误差最大为-1.38×10-5，下降阶段的网络预测误差最大为-2.39×10-5，这个精度还是比较高的，在实际工程应用中，可以将GRNN神经网络的预测输出用作GMM的期望输出。

2 BP神经网络非线性逼近

2.1 BP网络算法理论基础

假设一个含有隐含层的3层BP神经网络，输入层节点为xi，隐层节点为yj，输出节点为zl，θ为阈值函数，f为输入和输出之间的传递函数，输入节点与隐层节点间的网络权值为wj i，隐层节点与输出节点间的网络权值为vl j，输出节点的期望值为tl，则模型的计算公式为：

其中：

输出节点的输出为：

其中：

输出节点的误差为：

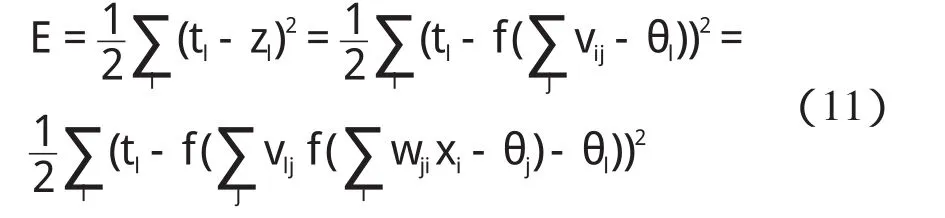
假设输入为磁场强度H，输出为GMM应变ε，则式（7）可变为：

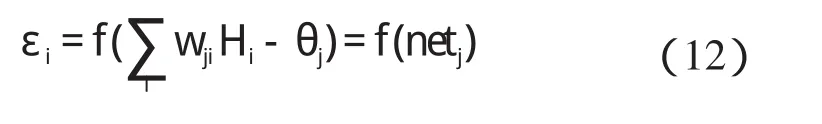
其中：

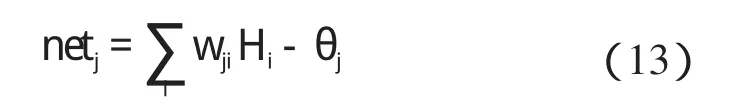
式（11）变为：

2.2 BP神经网络磁滞曲线拟合

在该部分，笔者同样将磁滞曲线分为磁场强度增加阶段和磁场强度减小阶段两部分，网络所用训练数据、测试数据与1.2节相同，网络的隐含层节点个数为5，输出层节点个数为1，网络的输出如图7～图10所示。

图7 磁场强度增加阶段BP网络预测输出

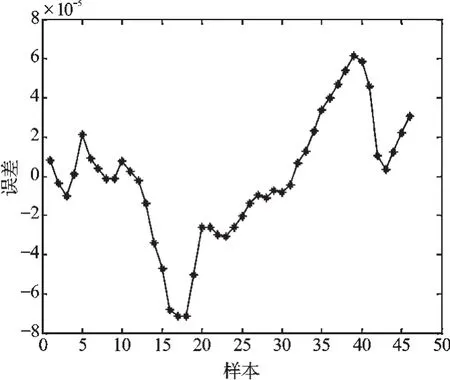
图8 磁场强度增加阶段BP网络预测误差

图9 磁场强度减小阶段BP网络预测输出

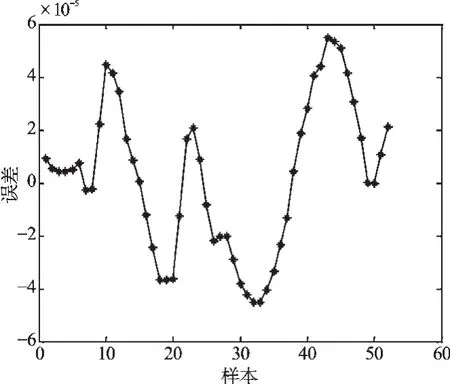
图10 磁场强度减小阶段BP网络预测误差

从图7～10中可以看出，BP神经网络的预测输出和实验实际输出相比，还是存在一定误差的，磁场强度增加阶段的最大网络预测误差为-7.18×10-5，磁场强度减小阶段网络的最大预测误差为-5.83×10-5，预测精度比GRNN神经网络略差。不过和J-A模型仿真曲线相比，BP神经网络的预测输出还是更接近于实验曲线，因此，在精度要求不是非常高的场合，可以用BP神经网络的预测输出来代替GMM的期望输出。

3 GRNN和BP神经网络的对比分析

为了便于观察最佳扩展系数下的GRNN神经网络和BP神经网络的预测效果，本研究对GRNN和BP网络进行预测对比分析，结果如图11所示。

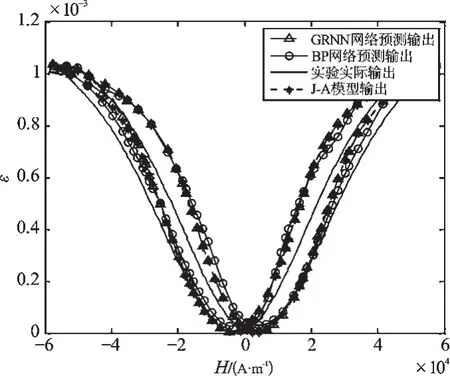
图11 GRNN和BP神经网络预测对比分析

从图11中可以看出，总体上来讲GRNN神经网络和BP神经网络的预测效果还是令人满意的，和J-A模型理论曲线相比，两种网络的预测都更接近于试验曲线。不过在磁场强度比较大的部分，BP神经网络的预测还存在较大误差。

为了更好地区别BP神经网络和优化后的GRNN神经网络间的拟合能力，这里再给出另一张Calkins试验曲线的拟合图，如图12、图13所示。

从图12、图13中可以看出，优化后的GRNN神经网络的预测能力明显好于BP神经网络。

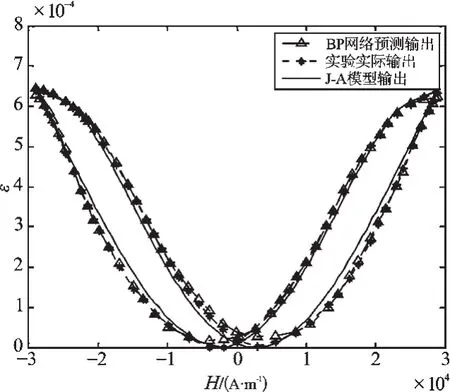
图12 BP神经网络预测输出

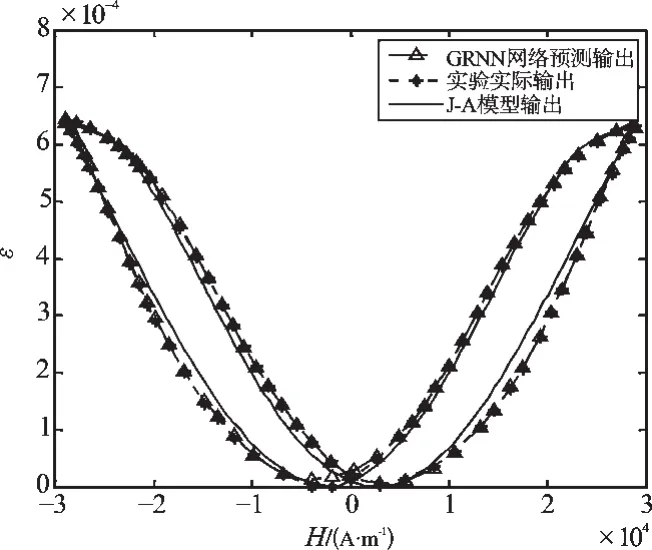
图13 GRNN神经网络预测输出

4 结束语

本研究用优化的广义回归神经网络GRNN和前馈神经网络BP分别对GMM的磁滞曲线进行了非线性拟合，并对两种拟合方法进行了对比，从对比中可以看出，两种网络的预测都取得了令人满意的效果。另外，采用循环算法求解SPREAD值的GRNN神经网络精度要略高些，不管是在加磁阶段，还是在退磁阶段，GRNN神经网络的预测误差都要低于BP神经网络，该研究可以为GMM的广泛应用提供很好的指导。

不过，GRNN神经网络的光滑性能（内退和外插能力）略差，因此，笔者将在未来的研究中，继续探索怎样更进一步优化和改进GRNN神经网络。

（References）：

[1] 卢全国.基于GMM的微致动研究及应用[D].武汉：武汉理工大学计算机科学与技术学院，2007.

[2] 董长虹.Matlab神经网络与应用[M].北京：国防工业出版社，2007.

[3] CINCOTTI S，MARCHESI M，SERRI A.A neural network model of parametric non-linear hysteretic inductors[J].IEEE Transactions on Magnetics，1998，34（2）：3040-3043.

[4] VECCHIO P D，SALVINI A.Neural network and fourrier descriptor macromodelin-g dynamic hysteresis[J].IEEE IEEE Transactionson Magnetics，2000，36 （4） ：1246-1249.

[5] MINCHEV S V.Neural networks for modeling of dynamic systems with hysteresis[C]//First International IEEE Sympo⁃sium"Inteligent Systems"，2002：42-47.

[6] MAKAVEEV D，DUPRE L，DE W M，et al.Dynamic hyster⁃esis modeling using feedforward neural network[C]//In 15th Solft Magnetic Confenence Abstract，Bilbao，2003：256-258.

[7] 李贵存，刘万顺，宫德锋，等.用于磁化曲线拟合的高精度混合型径向基函数神经网络[J].电网技术，2001，25（12）：18-21.

[8] 史 峰，王小川，郁 磊，等.MTALAB神经网络30个案例分析[M].北京：北京航空航天大学出版社，2010.

[9] CALKINS F T，SMITH R C.Energy-based hysteresis mod⁃el for magnetostrictive transducers[J].IEEE Transactions on Magnetics，2000，36（2）：429-439.

[10] CLARK A E.Magnetostrictive Rare Earth-Fe2Compounds，in Ferromagnetic Materials[M].E.P.Wohlfarth，Norh-Hol⁃land，Amsterdam，1980.

[11] JILES D C.Theory of the magnetomechanical effect[J].Journal of physics D:Applied physics，1999，32（15）：1537-1546.