四足机器人的爬-站运动模式转换研究*
周坤玲,张秀丽,龚加庆
(北京交通大学 机械与电子控制工程学院,北京 100044)
0 引 言
多肢动物的运动模式转换在自然界中非常常见,如猫、狗等四足动物在面对一些突发情况时,会即刻从四足爬行姿态转换成双足站立状态,以保证自身安全或完成目标动作。从人类行走功能的进化历程来看,从四足爬行到双足行走,经历了爬-站转换这一至关重要的过渡阶段。通过研究四足机器人的爬-站运动模式转换不仅可以丰富机器人的运动方式,拓展机器人对环境的适应范围,而且对于探索人类直立行走的生物学机理同样具有一定的启发意义。
对于足式机器人爬-站转换的研究最早见于1995年东京大学研制的双足机器人“Hanzou”[1]。Hanzou是一个具有16个自由度的仿人机器人,每条腿有4个自由度[2]。它通过改变踝关节和膝关节的角度来调整机器人的重心位置,通过手臂和腿的协调运动改变机器人的加速度,以实现俯卧、仰卧和侧卧3种情况下的爬-站运动模式转换。之后,法国凡尔赛大学[3]、日本产业技术综合研究所、京都大学、中国的西南大学、韩国科技院[4-6]等机构均进行过四足-双足爬站运动模式转换的研究和实验。
爬-站转换涉及复杂的运动过程,而轨迹规划是其中的关键技术之一。日本的HRP系列机器人[7-9]通过独立调节机器人各关节变量,实现了基于位置模式的爬-站转换轨迹规划,国内西南大学也进行过类似的研究[10]。这种方法的优点是比较直观,缺点是需要调节较多的参数。另一种方法是建立优化目标函数,对参数进行映射关联,通过调节少数几个参数实现爬-站转换轨迹规划,如京都大学[11-12]和索尼爱立信公司[13]针对双足机器人所做的研究。这种方法的优点是需要调节的参数少,不足之处是建立合理的目标函数相对困难,特别是对于变量之间还存在耦合的优化问题。
爬-站转换需要从四足支撑状态转换到双足支撑状态,在这个过程中由于支撑域减小,机器人极易出现失稳摔倒,因此转换过程中的平衡控制其关键所在。实现平衡控制的方法可以分为动平衡模式和静平衡模式两种。静态平衡控制一般应用于低速轻载情况下,一般采用CoM(center of mass)稳定判据,即将机器人重心控制在支撑域内;而动态平衡控制要考虑惯性力,一般采用ZMP(zero moment point)或CoP(center of pressure)作为判据,二者在某些情况下是重合的。索尼公司研制的 SDR[14-16]机器人、本田公司研制的ASIMO系列机器人、法国研制的NAO机器人[17-18]和上海交通大学研制的机器人[19-20]等均采用 ZMP 判据处理爬-站运动模式转换过程中的平衡控制。
目前,实现爬-站转换运动的机器人基本都是基于双足仿人机器人结构,而在四足机器人中比较少见。本研究针对一款12自由度仿生四足机器人Babybot,规划从四足站立状态到双足站立状态的运动转换过程,提出基于仿生和几何作图的轨迹规划与平衡控制方法。
1 四足机器人Babybot
Babybot是一个具有12个自由度的四足机器人,如图1所示。其躯干是刚性结构,每条腿有3个俯仰自由度,分别位于髋关节、膝关节和踝关节处。4条腿采用内膝肘式镜像关节配置模式,足底为平面。躯干长305 mm,宽320 mm,大腿长120 mm,小腿长135 mm,足长60 mm。
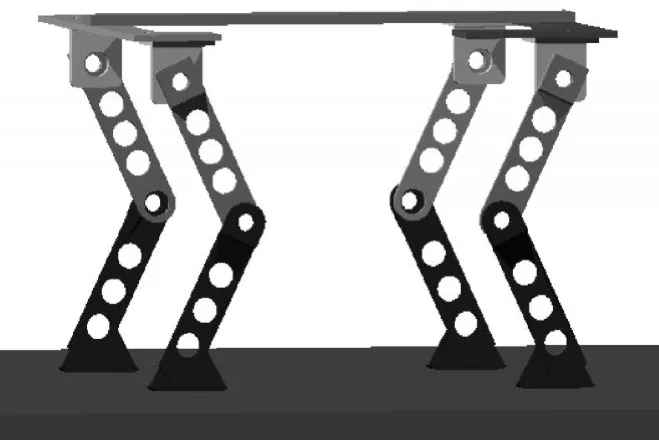
图1 Babybot四足机器人
由于四足机器人爬-站转换运动仅涉及侧平面的运动,本研究将机器人Babybot简化为平面内的六杆五自由度机构(小臂l1、大臂l2、躯干l3、大腿l4、小腿l5和足l6)。四足机器人坐标系如图2所示,箭头指向前进方向。
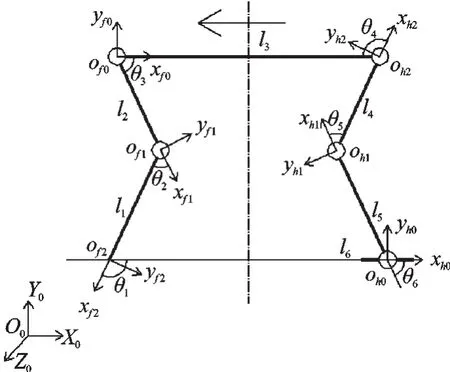
图2 四足机器人坐标系
图2中,∑0(O0,X0,Y0,Z0)为世界坐标系,依据D-H法建立各个连杆坐标系。关节转角为θj(j=1,2,…,6),连杆长度为li,质量为mi,杆件质心坐标为(xi,yi)(i=1,2,…,6),足长为l6,机器人双足站立时高度为h。
2 爬-站转换控制方法
通过仿生方法研究人类的爬-站转换运动规律,可以为四足机器人的爬-站转换轨迹规划提供设计依据。
2.1 人类的爬-站转换运动
将人的躯体结构简化为平面六杆五自由度机构,即小臂、大臂、躯干、大腿、小腿和足六部分,肘关节,肩关节、髋关节、膝关节和踝关节5个单自由度关节。用摄像机记录一位成年女性从四肢触地到双足站立的爬-站转换过程,提取运动过程中的6个关键帧,标记出关键帧中6根杆的位姿变化,其结果如图3所示。
记录整个站立过程中5个关节角及腕关节(小臂与水平地面之间的夹角)随时间的变化曲线如图4所示。
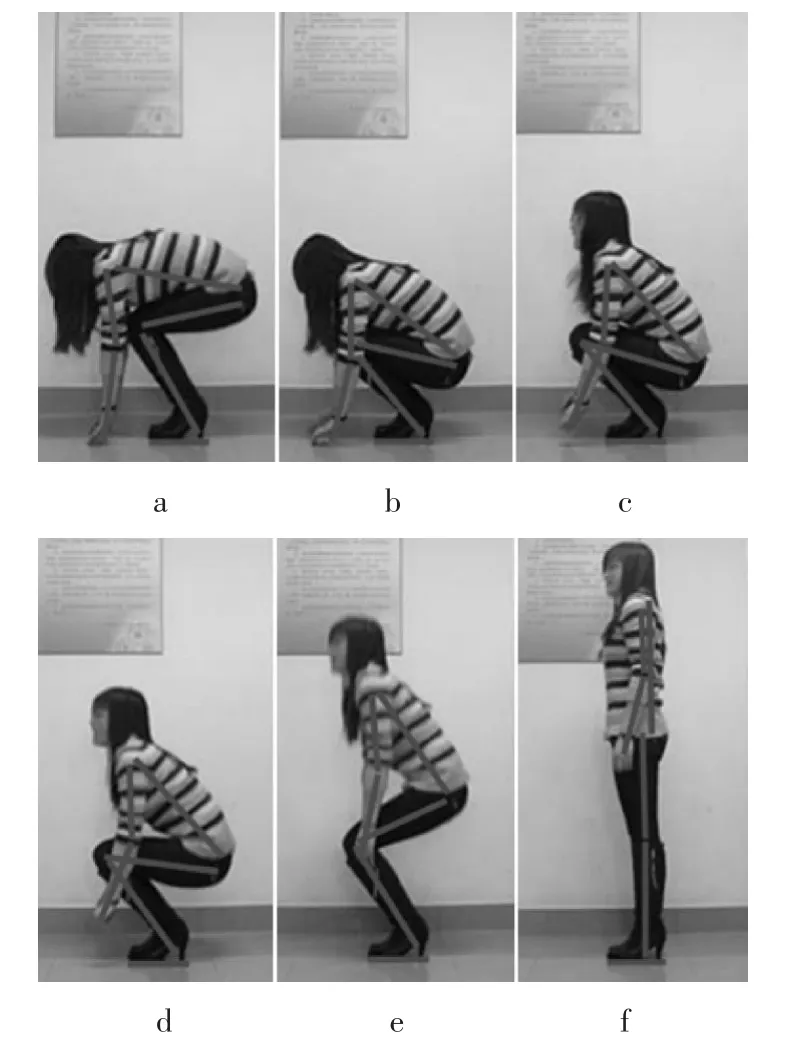
图3 人从四肢支撑到双足站立的过程
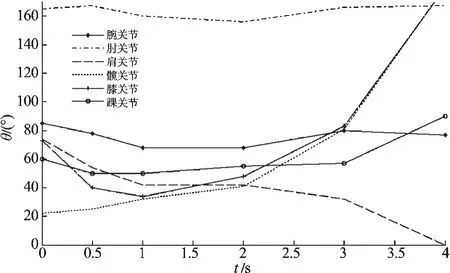
图4 关节角的变化曲线
分析图3和图4,可以得到以下规律:
(1)站立过程中,肘关节角θ2基本不变,手臂姿势保持不变;
(2)站立过程中,髋关节在竖直方向上有明显位置变化,先下降后上升,髋关节角θ4逐渐增大;
(3)在髋关节下降的过程中,肩关节角θ3逐渐减小至零,膝关节角θ5先减小后增大;
(4)站立过程中,踝关节角θ6逐渐增大至90°。
2.2 关节转角的轨迹规划
针对爬-站运动转换,四足机器人Babybot与人具有类似的简化机构,因此,借鉴2.1节得出的关节变化规律,可规划四足机器人Babybot爬-站运动模式转换过程中各关节转角的变化。本研究将机器人的爬-站运动模式转换分为两个步骤:
(1)双臂抬离地面,收至与躯干近似平行的位置,机器人由四足支撑转换为双足支撑;
(2)提升身体重心,完成整个站立过程。设定当h满足:(l3+l4+l5)×90%h(l3+l4+l5),则:机器人完成了爬-站运动模式转换。
2.2.1 前臂关节转角轨迹规划
以∑(Of0,Xf0,Yf0)为参考坐标系,θ1是手与水平地面之间的夹角,不需要考虑。根据2.1节仿生学调查得出的规律,设θ2为定值,腕关节的位置轨迹为直线,即:
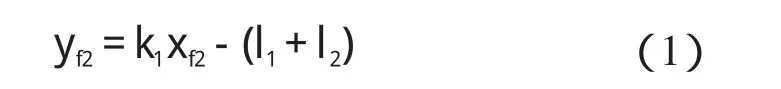
其中:k1=(l4+l5)/l3。
通过运动学逆解求肩关节转角θ3:
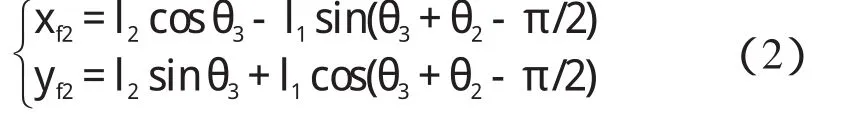
2.2.2 后腿关节转角轨迹规划
以∑(Oh0,Xh0,Yh0)为参考坐标系,采用多变量目标函数寻优方法,依据ZMP稳定判据建立优化目标函数,以求解后腿的关节转角θ4、θ5和θ6值。
计算ZMP点位置坐标为:
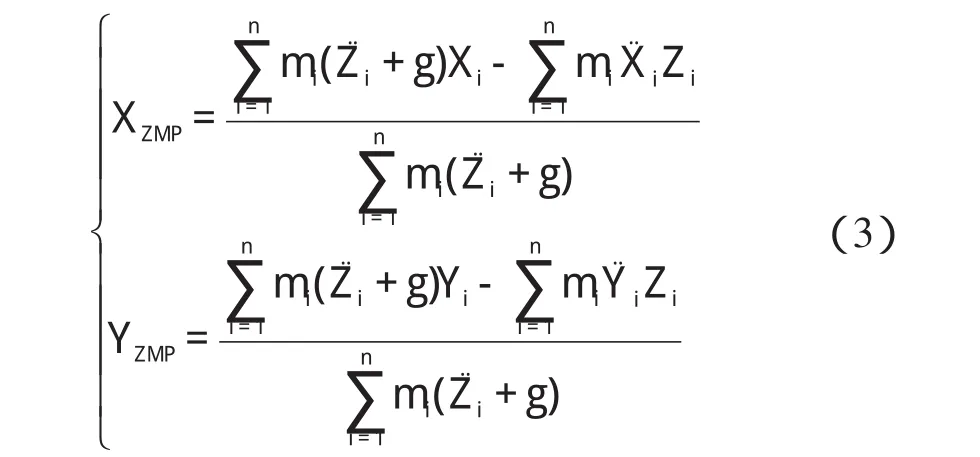
当机器人运动的速度和加速度较低时,接近静态运动,公式(3)简化为重心坐标计算公式:
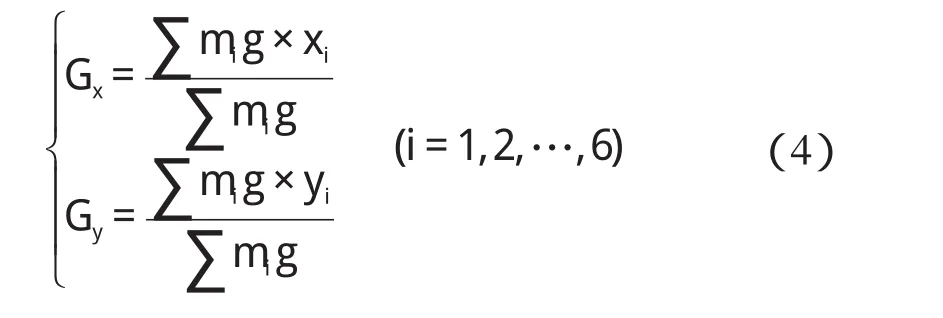
机器人四足支撑时,x向支撑边界为xlim=[-l3,a/2],双足支撑时,x向支撑边界为xlim=[-a/2,a/2]。针对爬-站转换的低速准静态运动,机器人保持身体平衡的条件是:

依据得出的规律,机器人进一步简化为五杆四自由度机构(手臂l1,2、躯干l3、大腿l4、小腿l5和足l6),则肩关节的运动轨迹为直线1(如图5所示);当θ6=90°时,髋关节的运动轨迹为半圆弧线(如图5所示)。
坐标系∑f0相对于坐标系∑h0的转换矩阵为:


图5 θ6=90°时的机器人位姿
肩关节、肘关节、腕关节在坐标系∑f0中用xf i表示,在坐标系∑h0中用表示,则:

肩关节和髋关节坐标满足:
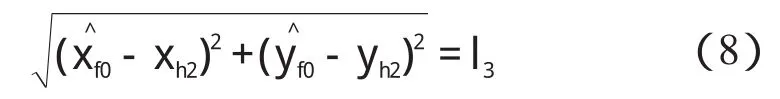
给出的约束条件如下:
(1)杆件l1、l2和l5在竖直方向上满足:

(2)肩关节的运动轨迹为水平直线,满足:

(3)髋关节的运动轨迹是以膝关节为圆心的圆弧线,满足:
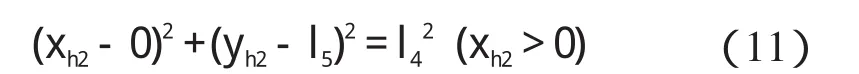
建立目标函数为:
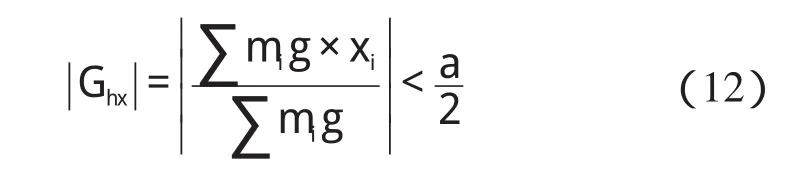
联立式(7~12),求得使 |Ghx|取得最小值时的θ4、θ5和θ6值。
若不能在“θ6=90°”的条件下,得到满足平衡条件的机器人姿态,则调整θ6值,使小腿l5向后倾斜,即θ690°。θ6≠ 90°时姿态如图6所示。肩关节的轨迹曲线仍为水平直线1,髋关节的轨迹曲线为虚线表示的新圆弧线。

新圆弧线为:

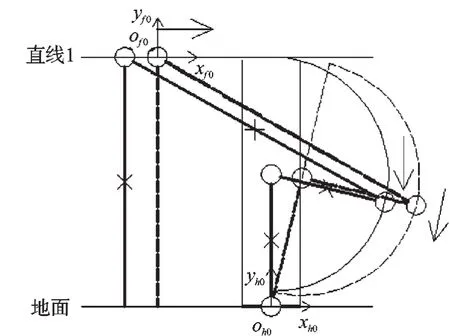
图6 θ6≠ 90°时姿态
联立式(6~10、12~14),求使 ||Ghx取得最小值时的θ4、θ5和θ6值,得到满足约束条件的机器人关键姿态。
通过上述方法寻优求解,可得到第1步调节所需的关节转角轨迹。机器人双臂抬离地面,收至与躯干近似平行的位置处,可完成四足支撑到双足支撑的转换。
在第2步调节中,机器人手臂和躯干无相对运动(θ2=C1,θ3=C2),因此机器人可近一步简化为四杆三自由度机构,如图7所示。
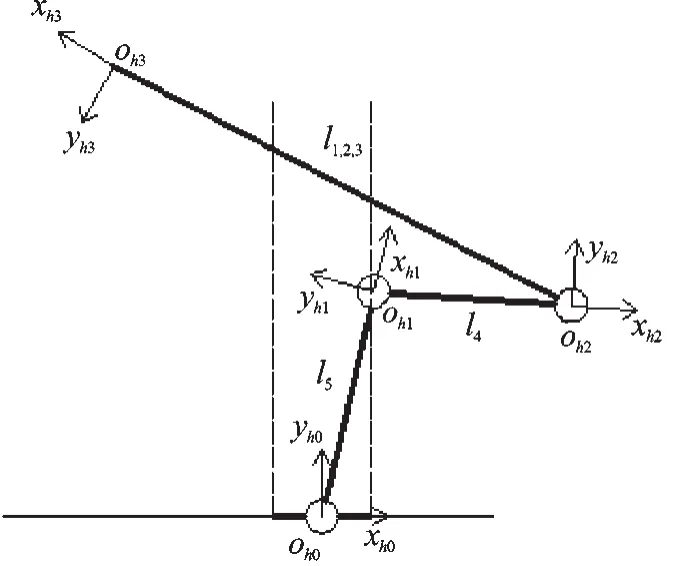
图7 四杆三自由度机构
以肩关节为末端执行器,运动轨迹为直线:
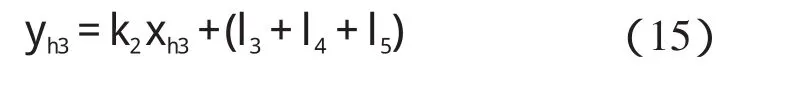
其中:
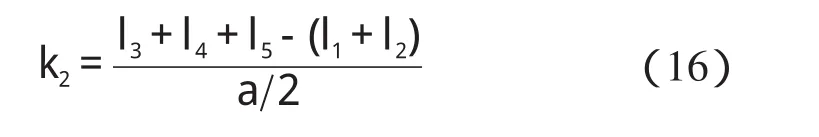
三自由度四杆机构运动学逆解公式为:
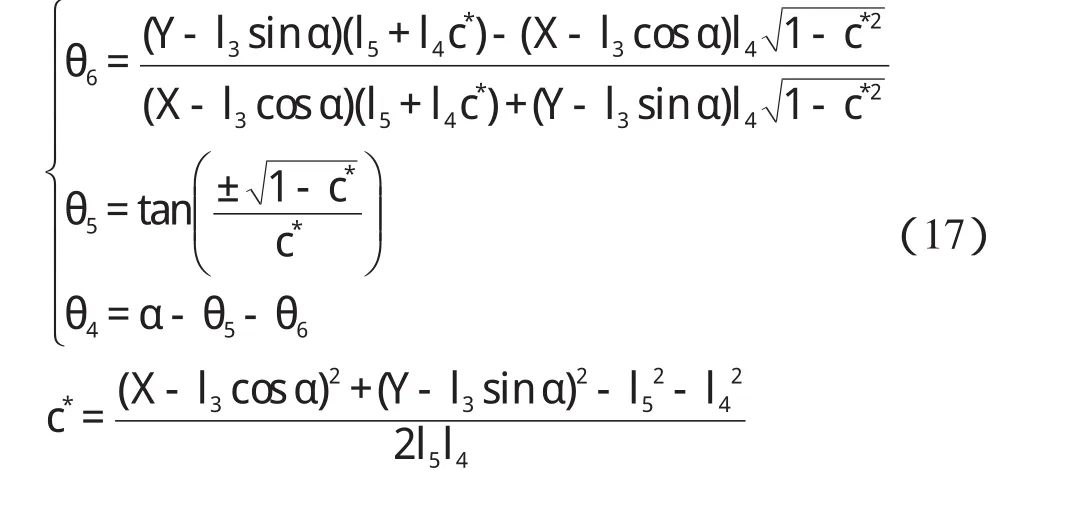
通过改变θ6的初始值,调节如图7所示姿态,联立式(15~17)求得满足目标函数式(12)的θ4、θ5和θ6值,以确定机器人在第2步调节中的关键姿态。
重复上述过程,得到n个关键位姿:
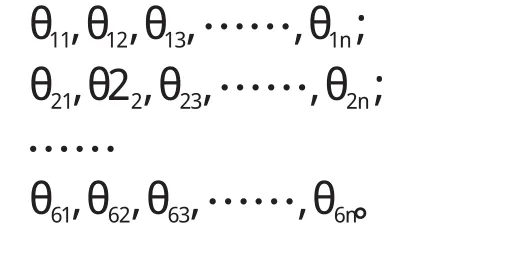
对θ11…θ1n,…,θ61…θ6n进行线性插值,实现相邻两个关键位姿之间的平稳过渡,得到四足机器人爬-站转换的关节转角的变化曲线,如图8所示。

图8 关节夹角变化曲线
3 动力学仿真
本研究利用ADAMS软件对Babybot机器人爬-站运动模式转换进行了动力学仿真研究。笔者设置足端与地面之间的接触碰撞模型中各参数值,以如图8所示6个关节转角的变化曲线作为对应关节的驱动函数,在动力学仿真中,Babybot用时9.5 s完成了爬-站运动模式的平滑转换,其结果如图9所示。
躯干质心的位移曲线如图10所示;在X方向上的速度和加速度曲线如图11所示。本研究通过上述曲线来评价Babybot机器人爬-站运动模式转换过程的稳定性。
图10中,两条虚线所夹范围是双足支撑稳定域,从0到右边虚线的范围是四足支撑的稳定域。在圆圈所示位置,机器人双臂抬离地面,由四足支撑转换为双足支撑,完成第1步调节。在第2步调节的过程中,躯干中心迅速提升,在X方向的位移波动处于支撑域内,表明机器人的运动过程是稳定的。
图11中,手臂抬离地面之前(点划线左边),机器人躯干迅速下降导致躯干质心的速度变化较大,但在该过程中,机器人处于四足支撑阶段,稳定域很大,结合图10可知,机器人的运动是稳定的。机器人双臂抬离地面造成躯干质心的加速度波动较剧烈,运动规划过程中,本研究采用了以支撑域为优化目标的规划方法,可使机器人获得最大稳定域,因此,机器人虽然出现轻微晃动,但是没有失稳。
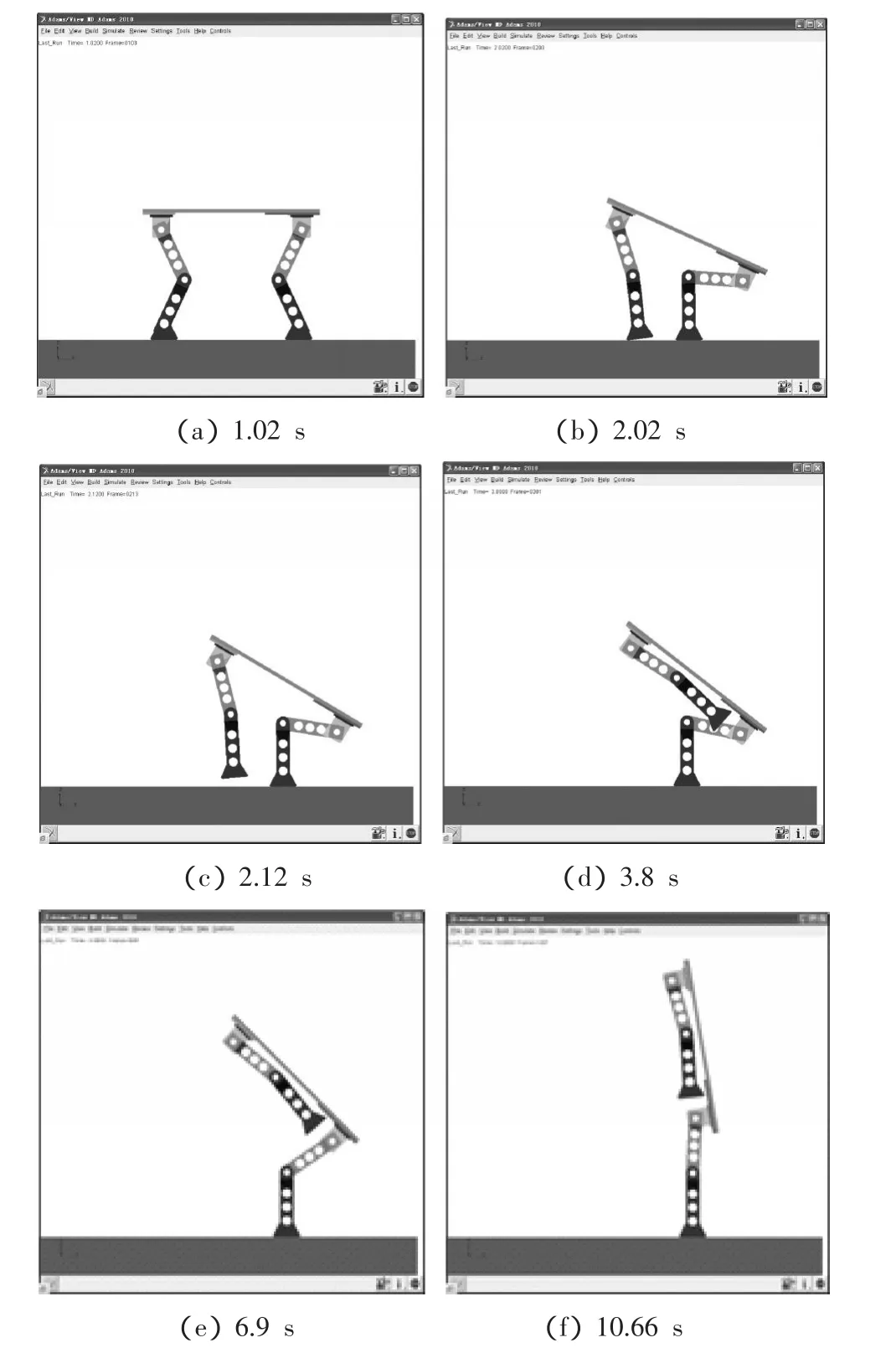
图9 Babybot爬-站转换动力学仿真
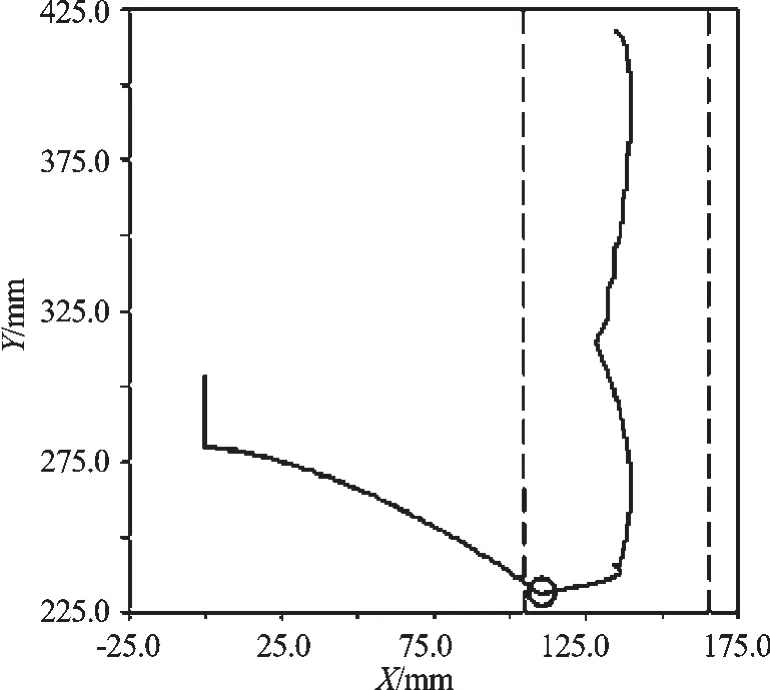
图10 躯干质心位移曲线
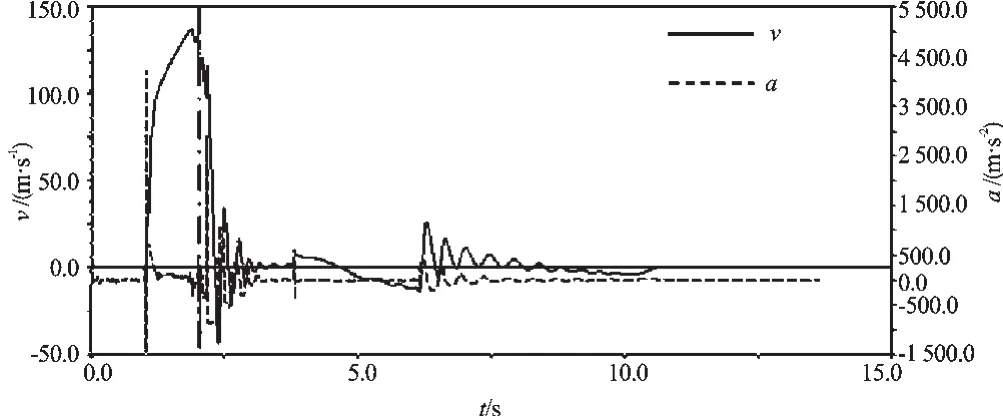
图11 躯干质心在X方向的速度、加速度曲线
4 结束语
本研究首先通过仿生学方法研究了人的爬-站转换运动,并从中提取出了一般规律,用于四足机器人Babybot爬-站运动模式转换过程的设计。将四足机器人简化为平面六杆五自由度机构,将几何作图法和基于ZMP稳定判据的优化设计方法相结合,进行了四足机器人的多自由度运动轨迹规划,以实现四足机器人的爬-站运动模式转换。在动力学仿真中,本研究所用的12自由度仿生四足机器人Babybot用时9.5 s完成了爬-站模式转换,验证了所提出的方法的有效性。
本研究提出的四足机器人爬站转换方法不仅可以用于丰富机器人的运动功能,拓展机器人对环境的适应范围,而且对于探索人类直立行走的生物学机理具有一定启发意义。
(
):
[1]INABA M,KANEHIRO F.Two-armed bipedal robot that can walk,roll over and stand up[C]//Proceedings of the 1995 IEEE/RSJ International Conference on Intelligent Robots and Systems.Published by the IEEE Computer Society,1995:297-302.
[2]KANEHIRO F,INABA M.Development of a two-armed bipedal robot that can walk and carry objects[C]//Proceedings of the 1996 IEEE/RSJ International Conference on Intelligent Robots and Systems,1996:23-28.
[3]GOUAILLIER D,HUGEL V,BLAZEVIC P,et al.The NAO humanoid:a combination of performance and affordability[J].Computing Research Repository,2008(1):1-10.
[4]KIM J H,OH J H.Walking control of the humanoid platform KHR-1 based on torque feedback control[C]//Proceedings of the 2004 IEEE/ICRA International Conference on Robotics & Automation,2004:623-628.
[5]KIM J Y,PARK I W.System design and dynamic walking of humanoid robot KHR-2[C]//Proceedings of the 2005 IEEE/ICRA International Conference on Robotics&Automation,2005:1431-1436.
[6]PARK I W,KIM J Y.mechanical design of humanoid robot platform KHR-3[C]//Proceedingsofthe 2005 5th IEEE-RAS international Conference on Humanoid Robots,2005:321-326.
[7]KANEHIRO F,KANEKO K.The first humanoid robot that has the same size as a human and that can lie down and get up[C]//Proceedings of the 2003 IEEE International Conference on Robotics & Automation,2003:1633-1639.
[8]KANEHIRO F,HIRUKAWA H.Locomotion planning of humanoid robots to pass through narrow spaces[C]//Proceedings of the 2004 IEEE International Conference on Robotics & Automation,2004:604-609.
[9]TANIE K.Humanoid robot and its Application Possibility[C]//Proceedings of the 2003 IEEE International Conference on Robotics,Intelligent System and Signal Processing,2003.
[10]蒲昌玖,王宇俊.一种双足机器人稳定起立方法研究[J].西南大学学报:自然科学版,2008,30(11):125-130.
[11]AOI S,EGI Y.Experimental verification of gait transition from quadrupedal to bipedal locomotion of an oscillator-driven biped robot[C]//Proceedings of the 2008 IEEE/RSJ International Conference on Intelligent Robots and Systems,2008:1115-1120.
[12]AOI S,TSUCHIYA K.Transition from quadrupedal to bipedal locomotion[C]//Proceedings of the 2005 IEEE/RSJ International Conference on Intelligent Robots and Systems,2005:3419-3424.
[13]ASA K,ISHIMURA K.Behavior transition between biped and quadruped walking by using bifurcation[J].Robotics and Autonomous Systems,2009,57(2):155-160.
[14]KUROKI Y,FUJITAL M.A small biped entertainment robot exploring attractive applications[C]//Proceedings of the 2003 IEEE International Conference on Robotics&Automation,2003:471-476.
[15]ISHIDA T,KUROKI Y.Development of mechanical system for a small biped entertainment robot[C]//Proceedings of the 2003 IEEE International Workshop on Robot and Human Interactive Communication,2003:297-302.
[16]FUJITA M,KUROKI Y.A small humanoid robot sdr-4x for entertainment applications[C]//Proceedings of the 2003 IEEE/ASME International Conference on Advanced Intelligent Mechatronics(AIM 2003),2003:938-943.
[17]GRAF C,HARTL A.A robust closed-loop gait for the standard platform league humanoid[C]//Proceedings of the 4th workshop on humanoid soccer robots.A workshop of the 2009 IEEE-RAS International Conference on Humanoid Robots,2009:30-37.
[18]GRAF C,ROFER T.A Closed-loop 3D-LIPM Gait for the RoboCup Standard Platform League Humanoid[C].In Proceedings of The Fourth Workshop on Humanoid Soccer Robots,2010.
[19]刘成刚,苏剑波.持续扰动下的仿人机器人站立平衡控制[C]//中国自动化学会控制理论专业委员会B卷,2011:3506-3511.
[20]XING Deng-ping,SU Jian-bo.Walking controllers under perturbations[C]//2011 IEEE International Conference on System,Man and Cybernetics,2011:1514-1519.

