在“自然拓展”中拔高案例解读

☉湖南省常德市芷兰实验学校初中部 陈金红

在“自然拓展”中拔高案例解读

☉湖南省常德市芷兰实验学校初中部 陈金红

“夯实基础，适时拔高”早已是老师们遵循“新课标”理念的基本决策，但如何“适时”却仍很茫然，不是硬塞、就是傻灌，使得学生一接触拔高的问题，要么不做、要么怕做，包括成绩好的都有不自觉的心理封闭；对策是如“润物细如声”消除恐惧心理，在不经意中“自然拓展”拔高，看课堂纪实.

一、拔高——自然拓展知识的内在联系

纪实环节：

师：如何求抛物线的解析式？

生1：设抛物线一般式y=ax2+bx+c的方法.

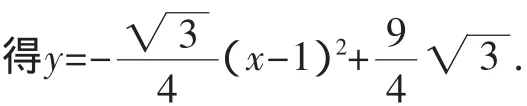
师：很好，大家实质上是用了一般式、顶点式和交点式三种不同的方法，不过三种形式是可以相互转化的！你觉得哪种方法对你来说简单些呢？又如何求抛物线的顶点呢？

生5（抢说）：一般式和交点式就只能硬用配方法了！但好麻烦的.

师（为打消埋怨！）：那好！是否可以找到绕开配方求顶点的方法呢？

师：生2、生3的方法都是从什么条件出发的？你受到何启发？

生7（顿悟）：都是从与x轴交点即点B、C入手的！即从交点式可得出顶点的横坐标x=1和对称轴.

生9：解析式不是交点式，而是一般式，又该如何求顶点呢？（挑战的口吻！）

师：同学们很不错，发现了由交点式可得出顶点式的妙法！要从一般式到达顶点式，除直接配方法外，还可充分利用交点式这个“中介”，你发现了什么？

生11：老师，如果一般式我们不能分解因式呢？如y=x2+ x+1（我们昨天做过了的一道题），开口向上，与x轴没有交点，与y轴交于点（0，1）.

生12：老师，上面的方法当Δ=b2-4ac＜0时就失效了！

师：不错！生12总结出与判别式有关系！当Δ＜0时，在实数范围内，此代数式不能因式分解，故我们由一般式得不出交点式！上面的方法就真的失效了吗？

师：抛物线的位置在什么变换时发生变化？

众生：哦！平移变换！

师：真棒！梳理一下刚才的思想方法，特别是绕开直接配方求顶点的方法！（抛物线y=ax2+bx+c，向下（c＞0）或向上（c＜0）平移个单位，得到y′=ax2+bx.右边因式分解得出与x轴的交点，再得出新抛物线的对称轴和顶点，最后向相反的方向向上或向下平移个单位，即得原抛物线对称轴（相同）、顶点坐标）

启示：在基础知识自然复习过程中，既有单项的温习，更有综合的联系，但探求联系的过程是自然的，尽管有认知冲突，但思想方法、主动探求意识自然流露；所以拔高就是自然拓展知识的内在联系！

二、拔高——自然拓展情感品质

案例2一次选用文［1］的一道思维挑战题作为数学课外活动题，活动花絮与体悟如下.

题目 关于x的方程x3-ax2-2ax+a2-1=0，只有一个实数根，则a的取值范围是______.

生甲：把左边写成一个关于x的一次因式与二次因式的积，且这个关于x的二次因式恰好无实数解，于是满足原方程只有一个实数根的条件，利用“待定系数法”求解.3222

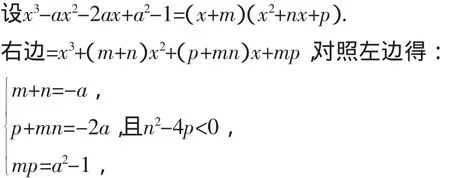
甲说好像进入“死胡同”，写不下去了！

生乙：初中没学一元三次方程的解法，故转换视角改写为关于a一元二次方程，利用“主元法”求解.

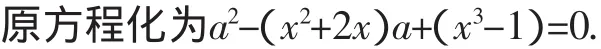
计算Δa=［-（x2+2x）］2-4（x3-1）=x4+4x2+4=（x2+2）2，发现始终有Δa＞0，即关于a的一元二次方程有两个不相等的值，转求a的范围时不知方向！

其后笔者和其上学生当面探讨了起来，作为老师，首要的应该是沿着学生的思路“走下去”，看看到底行不行，才能更好地肯定学生已有的正确认知和催生学生灵动的思维！于是有.

思路一：待定系数法

沿着甲的想法，困惑在于太多的辅助字母，自然想到减少辅助字母法；又注意到“关于x的方程x3-ax2-2ax+a2-1=0”的常数项a2-1因式分解为（a+1）（a-1），于是改进设法为：

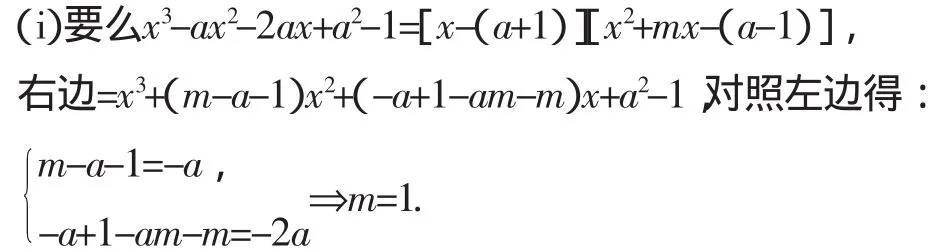
此时甲乐了，乙却急了，忙说老师我的呢？笔者笑着说：“不要急，我们接着往下看”.

思路二：“主元法”

此时乙对甲说，我就差那一小步！比你的思路更“大众化”！

笔者接着他俩的话茬，可见貌似“行不通”的方法，“迎难而上”有时亦可“破斧成舟、开天辟地”，顺着他人的思路“硬着头皮”展开探索，从中更能凸显思维的灵动与活力，彰显“坚持与坚守”的无穷魅力！接着启发学生：由求根公式导出的“源头”，你们可以想到什么新思路？

思路三：配方法

此时同学们不约而同地嘘嘘出：“好巧”，真逗的笑声！

启示：对学生流产的思路的“坚持与坚守”，既是一种人性的尊重与肯定，更是锲而不舍、勇往直前情操的历练，尤其是不可或缺的哲学思考！因此“坚持”的科学人文价值值得重视与开发！所以拔高就是自然拓展情感品质.

三、拔高——数据、数量自然解读中拓展信息达成一题多解（多变）

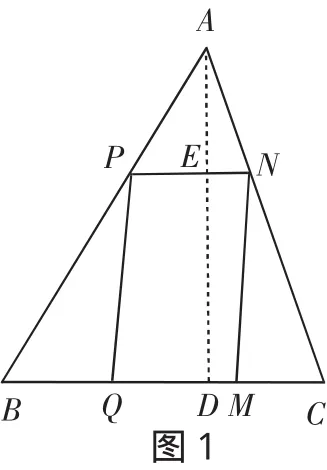
案例3相似三角形与二次函数的综合学习设计题目：如图1.▱PQMN内接于△ABC，QM在边BC上，另两个顶点P、N分别在AB、AC上，求证：▱PQMN的面积不大于△ABC的面积的一半.

分析：对数值“一半”、面积数量等自然解读，找出对应的概念、公式、定理信息，拓展产生不同的思路与方法.

思路一：局部观点与函数思想

（1）特值理解

（2）一般思考

局部观点即单独从平行四边形面积公式追溯.因▱PQMN的面积=底（PN）×高（DE），为找高作AD⊥BC交PN于E，垂足为D，设PN=x，AD=h，BC=a，▱PQMN的面积为S.

思路三：判别式法与化归思想

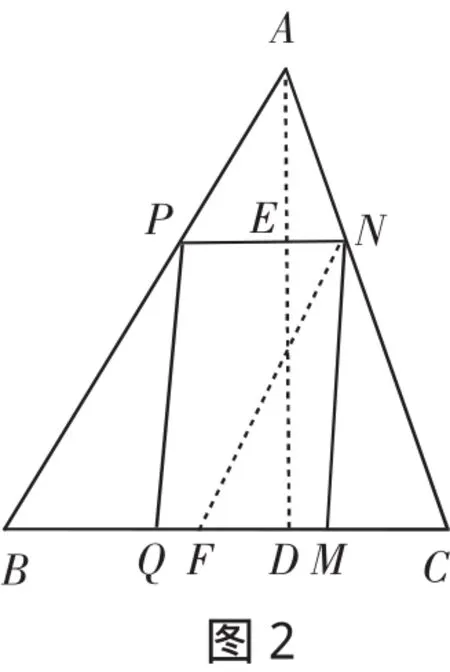
由图1知，S可用△ABC的面积减去△BPQ、△MNC、△APN的面积和；但在原图形中，只有△APN与△ABC相似，它们间的面积关系由相似定理易知.但△BPQ、△MNC与△ABC的面积关系表达繁琐困难，想到同类化归思想相似法可使面积关系表达变得容易，即过点N做NF∥AB交BC于点F，见图2.

因PN∥BC圯▱PBFN且它的面积等于S，于是△APN、△CFN均与△ABC相似.想到相似面积结论，于是再设△APN、△CFN的面积依次为S1、S2.

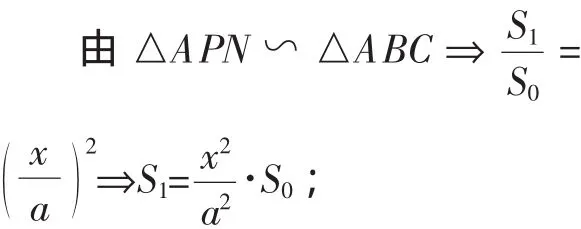
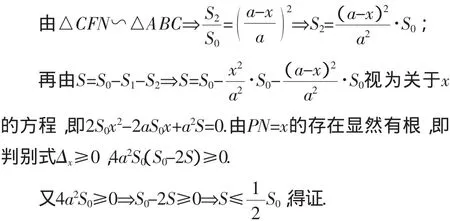
再问学生：还可以如何出题（变式）？

生1：▱PQMN变为矩形、正方形或菱形，其他条件不变，结论还成立吗？

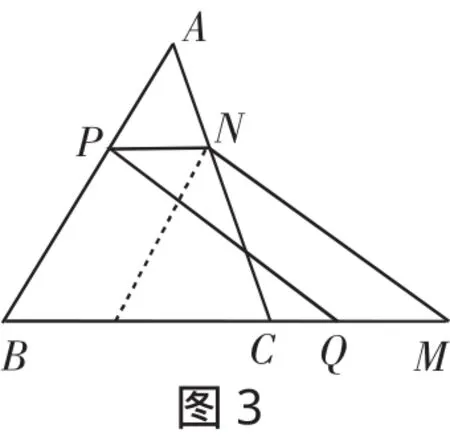
生2：QM在直线BC上，其他条件不变，结论还成立吗？见图3.

生3：在变式2中，▱PQMN变为矩形、正方形或菱形，其他条件不变，结论还成立吗？

生4：把原题中的▱PQMN变为两个全等的小平行四边形拼成的图形，其他条件不变，每个小的平行四边形的面积与△ABC的面积又有何关系？一般地变为n个全等的小平行四边形拼成的图形，又如何呢？

生5：类比变式2做变式4的思考，又如何？

生6：把原题中的▱PQMN变为内切圆，又如何？

运用特殊与一般、化归与分析的思想方法不难求解.

启示：探究是培养学生自主学习能力的一个重要环节.思想方法上常有特殊与一般相互转化、题组化的方法，现教材随处可见“思考”与“探究”字眼，如何准确把握与激励学生探究，则是课堂中师生互动的关键.所以拔高就是数据、数量自然解读中拓展信息达成一题多解（多变）.

1.马小为.中学数学解题思想方法技巧（初中）.西安：陕西师范大学出版社，2006（11）.

2.陈金红.迎难·就繁·挑战偶然和显然.中学数学教学参考（中旬），2010（9）.

3.陈金红.习题“磨”炼·结构“谋”法.中学数学（初中），2011（4）.