一种考虑风电随机性的机组组合模型及其算法

张宁宇 高 山 赵 欣

（东南大学电气工程学院 南京 210096）

1 引言

电力系统低碳化是指发展对环境、气候影响较小的新能源来替代传统高污染能源。新能源主要由两大类组成：一类是清洁能源，如核电、天然气等；另一类为可再生能源，如风能、太阳能、生物质能等。其中，风电以清洁、环保、绿色等特点成为学者关注的焦点，尤其经过近几十年的研究，风力发电技术得到了长足的发展，已有诸多国家实现了风电并网发电，但是风电完全替代火电等传统能源还存在着各种困难，因此，风电和火电、水电等同时并网发电将是电力系统在今后很长一段时间内需要面对的情况。

要保证风火并存电力系统安全稳定的运行，首先要在充分考虑风电随机性的基础上解决调度问题。传统的机组组合[1,2]（Unit Commitment，UC）模型在满足负荷平衡约束的前提下，只需针对负荷的预测误差和机组停运事故等提供相应的备用容量即可，而风电预测误差为 25%～40%[3]，远大于负荷预测误差 3%～5%，而目前为止备用容量一般由火电、水电机组提供，大规模风电场并网后，意味着需要启动更多的传统能源机组来保证系统安全稳定运行，这与新能源发展的初衷背道而驰。国内外关于此类问题的研究现状如下：文献[4]提出了一种电力市场体制下的机组组合随机模型，更新风电场的实际功率后重新计算未来时段的机组出力，是一种滚动优化方法。文献[5]从电力系统运行费用、可靠性和环境等方面研究了大规模风电并网对荷兰电网的影响，然后采用确定性UC-ED方法对火电机组的最优出力进行求解。文献[6]提出一种含风电场UC模型备用容量的计算方法，并将计算结果与传统算法进行了比较，其中采用情景树的方法来模拟风电场出力情况。文献[7]所述的UC模型通过随机抽样方法得到若干个风电功率情景，并采用Bender’s割将模型分解为主次两层，主模型用于求解机组的启停状态，次模型用于验证得到的启停状态在各种风电情景下是否满足网络安全等约束，如不满足则形成切割约束并返回主模型，如此循环直至求出最优解。文献[8]针对风电场出力的随机性，在风速预测的基础上，应用随机规划理论建立了电力系统动态经济调度模型，引入了机会规划约束条件，在求解模型时应用了综合随机模拟、神经元网络和遗传算法的混合智能算法。文献[9]所述的动态经济调度模型中引入了正、负旋转备用约束以应对风电功率预测误差给系统调度带来的影响，并提出了粒子群内点混合优化算法。文献[10]基于极限场景集的场景法来模拟风电功率的各种极限，并对包含各种风电功率极限的确定性机组组合模型采用混合整数规划方法求解。文献[11]使用机会约束规划方法来求解含风电场电力系统的备用容量，作者指出风电出力偏差概率分布应该介于正态分布和拉普拉斯分布之间，并通过选取合适的置信度水平求出了备用容量。文献[12]采用概率密度函数来分析负荷和风电出力的预测偏差，并引入到机组停运容量的计算中，最终采用智能优化算法求解出最优的旋转备用需求。

综上所述，含风电场机组组合问题的研究思路大致如下：将模型中的风电功率看作服从某种概率分布的随机变量，同时将包含该随机变量的约束条件用随机约束条件（一般为机会规划约束）替代，然后根据相关随机理论求解。根据随机约束条件处理方法的不同，模型求解算法可分为两类：第一类是利用概率论理论将随机约束条件机转换为确定性约束，然后由传统的数学规划方法求解，但在联合概率密度分布情况下，难以得到确定性模型；另一类方法利用了智能算法随机寻优的特点[13]，在每次得到新的个体后，进行随机约束条件验证，并通过惩罚因子的形式加入到目标函数中，但智能算法本身耗时较长，加入随机约束条件后将进一步影响计算效率。

针对已有模型和算法的不足，本文提出一种考虑风电随机性的机组组合模型及其算法，模型中引入风电可信度指标对风电功率随机变量建立机会约束条件，保证了系统运行的安全性。基于抽样平均逼近（Sample Average Approximation）理论，将上述模型转换成机组组合-抽样平均逼近（UCSAA）模型；通过 0/1辅助变量解决了联合概率密度分布的情况下UC模型难以求解的问题。

2 含风电场的机组组合模型

2.1 数学模型

（1）目标函数

（2）系统约束条件

功率平衡约束

备用约束

（3）机组约束条件

有功功率上下限约束：

最小开停机时间约束：

机组启动费用

（4）风电场投运容量约束条件

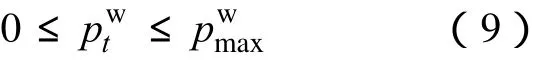
（5）风电可信度机会约束条件

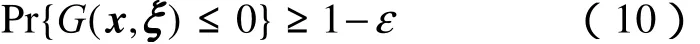
（6）网络安全约束条件

与现有UC模型将风电功率作为负的负荷从总负荷中减去的方法不同，本文模型将风电功率当作一个可调度量处理，同时在约束条件（3）中增加与风电场投运容量相关的备用容量，意义在于：随着风电场实际投运容量的增加，为保证系统运行的安全性，所需的备用容量也相应增加。此外，式（10）所示的风电可信度机会约束条件将风电功率投运容量与风电随机变量概率分布相关联，在风电可信度指标下实现风能最大化利用。

2.2 机会约束条件的处理

（1）策略1：

该策略从整个调度周期T上定义，表示旋转备用容量满足风电功率预测误差的概率不小于1-ε。

（2）策略2：

该策略从单个时间段上定义，保证单个时段中旋转备用容量满足风电功率预测误差的概率不小于1-ε。

（3）策略3：

上述三种策略中，由于策略3中的风电随机变量服从联合概率密度分布，因此，在相同风险度1-ε情况下，策略3最为严格，相应的运行费用也最大，在5.2节的算例分析中得到了验证。

3 抽样平均逼近方法（SAA）

3.1 机会约束规划[14]

对于式（1）～式（11）描述的随机规划问题，可用标准的机会约束规划模型表示为

式中，X⊂Rn，ξ为n维随机向量且服从联合概率密度分布，区间为Ξ，α∈ ( 0,1)，f∶Rn→R，G∶Rn×Ξ→Rm。

求解机会约束规划问题时，由于随机向量服从多维数的联合概率密度分布，即使模型（15）中约束条件的函数G(·,ξ)为最简单的线性函数，也难以通过数值方式直接处理机会约束。目前为止，比较有效的算法可分为两种：一种是离散采样法：对多维随机变量进行离散化处理，然后对得到的多个确定性模型求解；另一种方法是对模型（15）中的约束条件进行凸逼近处理得到确定性后求解。本文采用SAA算法属于后一种。

3.2 SAA算法

SAA算法是一种求解机会约束随机规划的有效算法，基本思路是：在经验分布条件下，使用Monte Carlo模拟技术得到随机变量概率分布的逼近表达式，然后对得到的模型进行求解。

采用SAA方法对式（15）中的机会约束条件转化得到到无穷大，SAA模型的解收敛于原模型，由于篇幅原因，对于证明过程本文不再赘述，具体可见文献[15]。此外在实际计算中，N一般取 2/α，γ取α/2。

4 含风电场机组组合问题的SAA模型

通过SAA算法对式（10）所示的机会规划约束处理得到式（19）后，便得到机组组合-抽样平均逼近模型，简称 UCSAA，目标函数为式（1），约束条件包含式（2）～式（9），以及式（21）。

可以看出，UCSAA模型中既包含机组启停整数变量，又含有机组有功输出等实数变量，属于混合整数规划（MIP）范畴。传统的MIP算法采用分支定界原理进行离散变量组合优化，由于存在“组合爆炸”问题，难以满足电力系统大规模优化的要求。但近几年，随着MIP算法的发展，特别是割平面算法、分支割平面算法的引入，MIP在求解大规模问题方面得到了长足进步，并已广泛应用于各种领域。因此，本文采用线性化 MIP算法来求解UCSAA模型。

线性化 MIP算法基于线性优化方法，在求解UCSAA模型时，需要所有非线性因素进行线性化逼近，包括发电成本曲线、开机费用和机组最小启停时间约束等。文中采用文献[16]所述的机组组合线性化模型，将式（1）～式（9）进行线性化。对式（21）进行线性化时，不同的风电可信度约束策略可采用不同的方法，具体如下：

（2）策略3：在这种情况下，因式（14）中随机变量服从联合概率密度分布，已不能通过策略 1和2采用的方法直接转换成确定性约束，为此，本文引入辅助变量，将式（14）转换成混合整数约束，具体模型如下[17]：

通过上述方法，式（22）～式（25）已转换成线性化模型，可以直接加入UCSAA的MIP模型中进行求解。UCSAA模型的MIP求解算法如图1所示。

算法流程中风电功率随机样本生成采用 Monte Carlo模拟实现。该方法是一种基于“随机数”的计算方法，可以有效模拟各种随机现象，常常作为一种计算标准来衡量其他随机方法。首先假设各时段风速服从联合威布尔概率密度分布，然后对风速随机向量进行采样，然后通过图2所示的风速-风电功率转换曲线计算风电功率样本。

图1 UCSAA模型的MIP算法流程Fig.1 Flow chart of MIP algorithm of UCSAA

图2 风力发电功率输出曲线Fig.2 The curve of wind turbine’s output

5 算例分析

本节分别采用了IEEE 3机和10机系统作为算例对UCSAA模型及其MIP算法进行了验证。IEEE 3机算例中对不同风电可信度以及三种策略情况下的模型最优解进行了求解，并对运行费用进行了比较；同时对不同抽样样本数N的情况下最优解的变化情况进行了分析，表明了算法的收敛性。10机算例中，对模型最优解的下限值进行了求解，并得到与最优解的间隙。硬件平台信息如下：CPU为酷睿双核，主频为2.8GHz，内存为2GB，程序开发环境为Matlab 2010b，MIP算法采用CPLEX 12.1混合整数规划软件包。

5.1 IEEE 3机6节点系统

机组参数和网络参数可见文献[18]，风电场的风机数量为50，通过节点4并网发电，单台风机的参数如下：切入风速 3m/s，额定风速 13.5m/s，切出风速20m/s，额定功率1MW，24个时段的风速预测值见表 1，标准差取预测值的 0.2～0.4。MIP算法参数如下：β取0.4，ˆS为10，M为10，N取20，γ取α/2。

表1 24小时风速预测值Tab.1 24 hour forecast data of wind speed

表2 策略1情况下的计算结果Tab.2 Results of policy 1

表3 策略2情况下的计算结果Tab.3 Results of policy 2

表4 策略3情况下的计算结果Tab.4 Results of policy 3

三种策略下系统的运行费用变化情况见表 2～表4所示。随着风电功率不满足概率从15%增加到90%，系统的运行费用随着风电穿透的增加而逐渐减小，这与机会约束规划风险越大，收益越大的规律相符。相同的风电可信度指标情况下，策略1的运行费用最小，策略2次之，策略3最大，这是因为策略 3中考虑了随机向量ξ服从联合概率密度分布，式（14）从整个规划周期上对风电投运容量做出限制导致的，同时也表明式（22）～式（25）可以有效地处理联合概率密度分布下的机会约束条件。此外，三种策略下的弃风量分别从风电不满足概率为15%时的707.7MW、1104.2MW和1104.2MW减少到90%时的394.6MW、78.7MW和763.1MW，虽然减少了风电能源浪费，但同时电力系统的运行风险有所增加，其中策略2情况下增加的运行风险大于其他两种策略。从运行时间上来看，除了策略3因引入较多辅助变量导致运行时间较长外，策略1和2情况下，计算时间均小于1s。

风机数量为70台，风电不满足概率为45%时，三种策略下的计算结果见表5。与风机数量为50台时的计算结果相比，运行费用有所减少，风电穿透率和弃风量相应增加，计算时间变化不大，表明本文模型在不同并网风机数情况下具有不同的计算结果。

表5 三种策略情况下的计算结果比较Tab.5 The comparison of results by three policies

在策略 2的情况下，UCSAA模型的最优解与随机向量的采样样本数N的关系如图3所示。可见，随着N的增加，最优解呈收敛特性，充分验证了SAA方法的正确性和有效性。

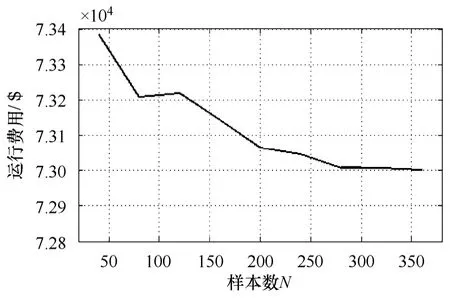
图3 UCSAA模型的最优解与样本数N的关系Fig.3 The relationship between the optimal result of UCSAA and sample number N

5.2 IEEE10机系统

算例数据可见文献[19]，风电场的风机数量为300台，其余参数与5.1节中相同，τ取0.01，L可根据 3.2节中相应计算公式得到。在不同样本数N和风电投运风险度ε的情况下，对采用第三种策略的UCSAA模型进行求解，计算结果见表6。

表6 10机系统计算结果Tab.6 Results of 10-unit system

由表6可见，图1所示的MIP算法可以有效的求出UCSAA模型最优解的下限值，在不同样本数N情况下，解间隙略有不同。

6 结论

文中提出的含风电场随机机组组合模型，使用SAA方法处理机会约束条件，从而得到UCSAA模型，尤其在随机变量服从联合概率密度分布的情况下，可通过引入 0/1辅助变量将机会约束转换成确定性约束。对 UCSAA模型的线性化后，直接采用MIP规划方法进行求解。最后，通过对不同算例进行仿真计算，表明所述模型及算法的有效性和正确性。

[1] 黎静华, 韦化. 基于模式搜索算法的电力系统机组组合问题[J]. 电工技术学报, 2009, 24(6): 121-128.Li Jinghua, Wei Hua. A general pattern search algorithm for electric power system unit commitment problems[J]. Transactions of China Electrotechnical Society, 2009, 24(6): 121-128.

[2] 江全元, 张铭泽, 高强. 考虑交流潮流约束的机组组合并行解法[J]. 电工技术学报, 2009, 24(8):120-126.Jiang Quanyuan, Zhang Mingze, Gao Qiang. A parallel algorithm for unit commitment including ac power flow constraints[J]. Transactions of China Electrotechnical Society, 2009, 24(8): 120-126.

[3] 杨秀媛, 肖洋, 陈树勇. 风电场风速和发电功率预测研究[J]. 中国电机工程学报, 2005, 25(11): 1-5.Yang Xiuyuan, XiaoYang, Chen Shuyong. Wind speed and generated power forecasting in wind farm[J]. Proceedings of the CSEE, 2005, 25(11):1-5.

[4] A Tuohy, P Meibom, E Denny, et al. Unit commitment for systems with significant wind penetration[J]. IEEE Transactions on Power System,2009, 24(2): 592-601.

[5] B C Ummels, M Gibescu, E Pelgrum, et al. Impacts of wind power on thermal generation unit commitment and dispatch[J]. IEEE Transactions on Energy Conversim, 2007, 22(1): 44-51.

[6] F Bouffard, F D Galiana. Stochastic security for operations planning with significant wind power generation[C]. IEEE Power and Energy Society General Meeting-Conversion and Delivery of Electrical Energy in the 21st Century, Pittsburgh, PA,2008.

[7] J Wang, M Shahidehpour, Z Li. Security-constrained unit commitment with volatile wind power generation[J]. IEEE Transactions on Power System,2008, 23(3): 1319-1327.

[8] 孙元章, 吴俊, 李国杰. 基于风速预测和随机规划的含风电场电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(4): 41-47.Sun Yuanzhang, Wu Jun, Li Guojie. Dynamic economic dispatch considering wind power penetration based on wind speed forecasting and stochastic programming[J]. Proceedings of the CSEE,2009, 29(4): 41-47.

[9] 周玮, 彭昱, 孙辉. 含风电场的电力系统动态经济调度[J]. 中国电机工程学报, 2009, 29(25) : 13-18.Zhou Wei, Peng Yu, Sun Hui, et al. Dynamic economic dispatch in wind power integrated system[J]. Proceedings of the CSEE, 2009, 29(25): 13-18

[10] 叶荣, 陈皓勇, 王钢. 多风电场并网时安全约束机组组合的混合整数规划解法[J]. 电力系统自动化,2010, 34(5): 29-33.Ye Rong, Chen Haoyong, Wang Gang. A mixed integer programming method for security-constrained unit commitment with multiple wind farms[J].Automation of Electric Power Systems, 2010, 34(5):29-33.

[11] 葛炬, 王飞, 张粒子. 含风电场电力系统旋转备用获取模型[J]. 电力系统自动化, 2010, 30(6): 32-36.Ge Ju, Wang Fei, Zhang Lizi. Spinning reserve model in the wind power integrated power system [J] .Automation of Electric Power Systems, 2010, 30(6):32-36.

[12] 苏鹏, 刘天琪, 李兴源. 含风电的系统最优旋转备用的确定[J]. 中国电机工程学报, 2010, 34(12):158-162.Su Peng, Liu Tianqi, Li Xingyuan. Determination of optimal spinning reserve of power grid containing wind[J]. Power System Technology, 2010, 34(12):158-162.

[13] 江岳文, 陈冲, 温步瀛. 含风电场的电力系统机组组合问题随机模拟粒子群算法[J]. 电工技术学报,2009, 24(6): 129-137.Jiang Yuewen, Chen Chong, Wen Buying. Particle swarm research of stochastic simulation for unit commitmen in wind farms integrated power system[J]. Transactions of China Electrotechnical Society,2009, 24(6): 129-137.

[14] B K Pagnoncelli, S Ahmed, A Shapiro. Sample average approximation method for chance constrained programming: theory and applications[J]. Journal Optimization Theory Applications, 2009, 142 (2):399-416.

[15] Wang Qianfan, Guan Yongpei, Wang Jionhui. A chance-constrained two-stage stochastic program for unit commitment with uncertain wind power output[J].IEEE Transactions on Power Systems, 2012, 27(1):206-215.

[16] Carrion M, Arroyo J M. A computationally efficient mixed-integer linear formulation for the thermal unit commitment problem[J]. IEEE Transactions on Power Systems, 2006, 21(3): 1371-1378.

[17] Luedtke J, Ahmed S. An integer programming approach for linear programs with probabilistic constraints[C]. Integer Programming and Combinatorial Optimization, Ithaca, USA, 2007.

[18] Yong Fu, Shahidehpour M. Security-constrained unit commitment with AC constraints[J]. IEEE Transactions on Power Systems, 2005, 20 (3): 1538-1550.

[19] Weerakorn Ongsakul, Nit Petcharaks. Unit commitment by enhanced adaptive lagrangian relaxation[J]. IEEE Transactions on Power Systems, 2004, 19(1):620-628.