基于空间相关法的风电场风速多步预测模型

陈妮亚 钱 政 孟晓风 孟凯峰

（1. 北京航空航天大学仪器科学与光电工程学院 北京 100191 2. 中能电力科技开发有限公司 北京 100191）

1 引言

风力发电由于其环保、可再生等诸多优势，近年来发展迅速，已经成为公认的理想能源[1]。截至2011年底，全球风电装机量已达 238GW，其中中国以26.3%的比例，成为装机量第一的风电大国[2]。由于风力具有很大的随机性和不可控性，随之风电场的输出功率也有波动性和间歇性的特点，从而导致电网调峰、无功及电压控制方面的困难，影响了电网的安全稳定，更限制了风电的发展。因此，通过对风电功率的准确预测，能够有效降低风电不确定性的影响，从而为电力部门制定合理调度计划提供保障[3,4]。

风机发电功率最主要的决定因素是当地的风速，故对风速的有效预测是预测风电功率的关键环节。目前，国内外对风速预测的研究主要分为两大类：基于历史数据建模的统计学方法、基于数值天气预报及地形学等的物理方法。前者主要包括时间序列法[5,6]、卡尔曼滤波[7]、神经网络法[8-10]、支持向量机[11,12]等，建模较为简洁，计算速度快，但预测精度随着预测时间的增加而急剧下降。物理方法则主要包括基于数值天气预报（NWP）的预测模型[13-15]、空间相关法[16,17]。基于数值天气预报的模型可得到未来1～3天的风电预测值，其预测精度较为稳定，但计算量庞大，常需要巨型计算机连续运算数小时。空间相关法基于风电场周边测风站点的风速数据建立空间相关模型以预测未来数小时的风速，因可预知风速变化趋势，该方法的预测精度较高，但受测风站位置、风向变化影响较大。

本文在分析了相邻测风站点的风速序列相似性特征后，提出了基于相关系数判据确定模型输入的方法，可有效降低测风站距离远近的影响，从而建立精确的分风向空间相关模型。之后再将其与支持向量机预测法相结合，得到新的混合模型，用于风速的多小时预测。空间相关模型通过上风向测风站的数据可获取未来几小时的风速变化趋势，故多小时预测精度较高，但其受风向影响较大，可能出现预测误差极大点。而支持向量机方法的预测误差与风向无明显相关关系，预测性能较为稳定。因此，结合空间相关法与支持向量机的优点，即可得到高精度、性能稳定的混合模型。

本文针对某风电场的实际情况，选取了其周边数十公里处、位于相反方向上的两个测风塔，并分别建立空间相关模型，以预测未来数小时的风速小时均值。在详细分析风向变化与预测误差关系后，文中将 SVM 方法与空间相关模型结合，得到混合模型。最终，将预测结果与实测数据相比较，可证实混合模型的准确性。

2 风速多小时预测模型

2.1 空间相关法

2.1.1 风速的空间相关性

本文将所选取的风电场周边测风塔命名为站点S1、S2，风电场内的测风塔命名为站点W。三站点呈近似直线排列，其中，站点W位于中间位置，站点S1位于W正北偏西53°方向，距离约56km；站点 S2位于 W 正北偏东 129°方向，间距约为51km。

由于风速本身固有的物理特性与地形的影响，同一风向上不同地点间的风速变化曲线不可能完全相同，但往往表现出很强的相似性和延时性[18]。三站点某时段的风速变化图如图1所示。

图1 站点S1、S2、W的风速变化曲线Fig.1 Wind speed curve of site S1, S2 and W

由图1可见，三个站点的风速变化曲线有着明显的相似性，且由于 S1位于 W 的上风向，故 S1曲线超前于W曲线，同样W曲线超前于S2曲线。因而，可以利用此超前性，使用站点 S1的历史测风数据得到站点W未来几小时的风速变化趋势。同理，当风向转为逆向时，S2风速变化曲线应超前，则可利用S2的历史风速数据预测W的风速。

2.1.2 相邻站点的相关系数

由上文知，同一风向上不同地点的风速曲线具有明显的相似性及延时性。若测风站点间地形平坦，则S1在W上风向时，理想情况下有

式中，L为S1、W之间的距离。事实上，S1与W之间的风速关系由于地形、气流的影响不可能呈现完全的线性关系，但大致趋势与此类似。

由式（1），在t时刻预测站点W的t+s风速值，需输入站点S1在t+s-Δt时刻的风速、风向序列。但实际中Δt受到诸多因素如风速、风向以及环境、气流等因素影响，很难计算。本文中，提出一种使用相关系数作为判据确定Δt的方法。

相关系数是用来评价两组数据序列的相似性的判据，在t时刻站点S1与站点W风速序列的相关系数计算式为

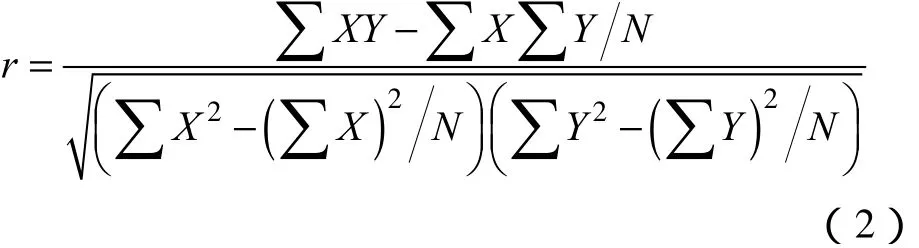
式中，N为风速序列的长度，且

当Δt变化时，r的值也随之变化。图2中绘出站点S1和站点W的风速序列相关系数值r随Δt的变化曲线。

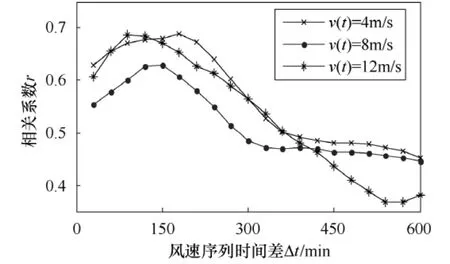
图2 站点S1与W的风速序列相关系数Fig.2 Correlation coefficient of wind speed series in site S1, W

易知，相关系数极值点处对应的Δt代表了在此时间差下，两站点的风速序列最为相似。由图中可看出，当风速值较小时，极值点对应的时间差Δt较大，即此时气流需更多的时间由站点 S1流向 W，符合气流的自然流动特征。这也证明了由相关系数作为判据求得Δt的方法是可行的。

2.1.3 基于BP神经网络的分风向空间相关模型

BP（Back Propagation）网络最初由Rumelhart为首的研究小组提出，是一种按误差逆传播算法训练的多层前馈网络[19]。BP网络作为目前应用最广泛的神经网络方法之一，有着学习速度快、非线性拟合精度高等优点，故本文用该方法建立相邻测风站点间的空间相关模型。

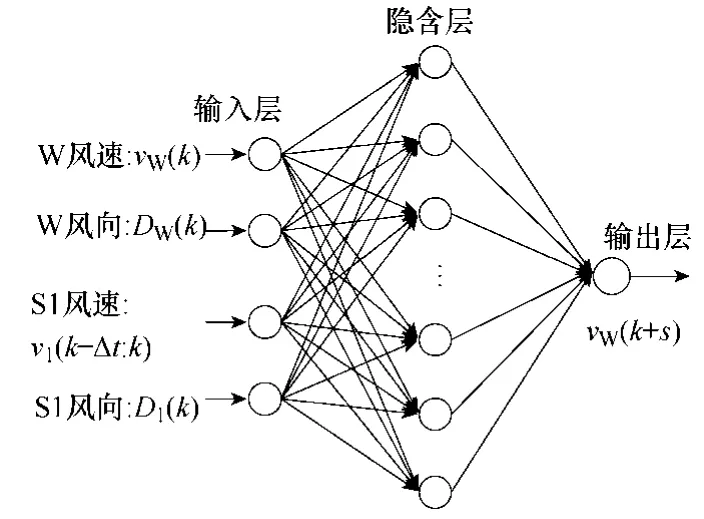
图3 基于BP网络的空间相关模型结构图Fig.3 Spatial correlation model based on BP network

以使用测风站点 S1建立模型为例，空间相关模型的结构如图3所示。该模型在k时刻的输入为：站点W的当前风速、风向，站点S1从相关系数曲线极值点对应的k-Δt时刻到k时刻的风速、k时刻风向；输出为对站点W的风速预测值vW(k+s)，其中s为预测步长。

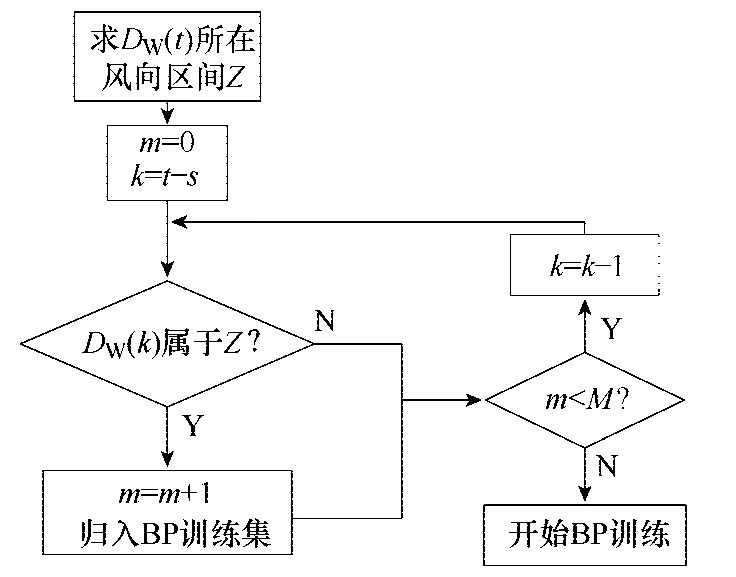
图4 分风向空间相关模型的建模流程图Fig.4 Flow chart of spatial correlation model

如上文所述，每次进行风速预测均实时建模，且使用与当前时刻处于相同风向区间的测风数据作为训练集，故站点间的风速相关关系类似，更易于建立起准确的空间相关模型。建立当前时刻的训练集后，BP网络根据对训练集的预测误差自动调节网络权值，最终得到使预测误差最小的空间相关模型，从而由站点S1与W的历史风速值计算出对站点W的预测值。

2.2 支持向量机（SVM）模型

支持向量机由于其优越的非线性拟合性能，近年来得到了广泛的应用，其基本思想是：通过某种事先选择的非线性映射将输入向量x映射到一个高维的特征空间Z，并在此空间中构造最优分类超平面[20]。

使得如下的风险函数最小化并满足约束

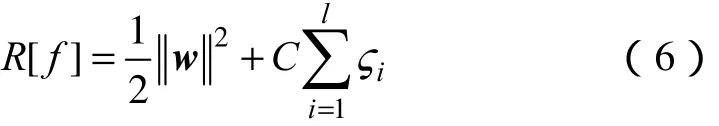
式中，w为控制模型的平滑度；g(x) 为输入空间到特征空间的函数；b是偏移量；C为调整系数；iς是所选取的损失函数。通常，此最优化问题由拉格朗日方程求解，具体过程可参见文献[21]。

2.3 多小时预测混合模型

上文中分别基于空间相关法与 SVM 建立了风速预测模型，但是，它们都有着各自的优缺点。为分析两种模型的预测性能差异，对该风场2011年的风速数据作2h预测仿真，以风向20°为一区间，可绘出平均预测误差与 W 当前时刻风向角度的关系曲线如图5所示。

图5 风速2h预测误差曲线Fig.5 Two hour ahead wind speed forecasting error

图中的两条虚线分别代表主风向与 S1、S2所在方位重合时的风向角。由图中明显可以看出，当风向与测风塔方位越接近时，空间相关模型的优势越突出；但偏离较远时，如风向为正北偏西 300°左右时，空间相关模型出现了误差极值点，说明此时加入周边测风塔的风速信息反而会干扰预测模型的正常建立，导致误差的较大波动。

由上，分风向空间相关模型的多小时预测精度较高，但因受限于数据来源，预测性能依赖于主风向的变化，当主风向与测风站点连线相差较大时，预测误差随之剧增，可能出现一些误差极大的不合理预测值。SVM模型的平均预测精度不及空间相关法，但预测性能稳定。故本文结合以上两种模型的优点，建立了一种新的混合模型，结构图如图6所示。

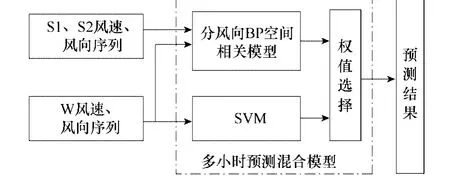
图6 风速预测混合模型的系统框图Fig.6 Structure of hybrid wind speed prediction model

如图6所示，混合模型以分风向 BP空间相关模型及 SVM 模型的预测值为输入，建立权值选择机制，所输出的预测结果为

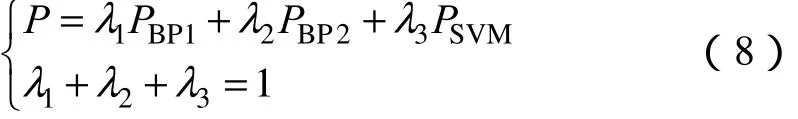
式中，λ1、λ2、λ3为权值系数。

由于空间相关法的预测误差主要取决于当前的主风向，而 SVM 模型的预测误差主要取决于预测时长，故权值的计算需按风向与预测时间分类。

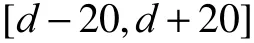
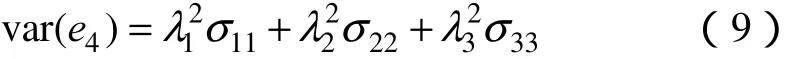
在约束λ1+λ2+λ3=1条件下，即可使用拉格朗日法求得var(e4)的极小值，从而计算出权值系数。

3 风速预测实例

本文研究验证的数据库为某风电场及其周边 2个测风站2010年1月至2011年7月的实测数据。为建模的准确、便利，监测数据经过以下预处理：滤除噪声点、线性插值、按小时平均。

3.1 建模流程

鉴于风速数据历史数据库十分庞大，以站点S1、W的1 200h测风数据作为训练集，在t时刻作一小时预测为例，建模流程如下：

（1）绘制t时刻站点S1与W的风速序列相关曲线，求得极值点对应的时间差Δt。

（2）判定t时刻W站点风向所在的风向区间，以t-599至t时刻数据中属于相应区间的子数据库为训练集，建立BP空间相关模型，得到t+1时刻的风速均值。

（3）以t-599至t时刻共600h的数据为训练集，建立SVM一步预测模型，得到t+1时刻的风速均值。

（4）以t-1 200+i至t-601+i时刻的数据为训练集，分别得到两模型对t-600+i时刻的预测序列，其中i=1,2,…,600。将预测序列与实测值作差，计算出两模型的误差序列。

（5）按t时刻的风向从上一步中的误差序列选择出对应的误差子序列，计算权值系数，得到混合模型对t+1时刻的预测值。

（6）将混合模型的预测值与t+1时刻的实测值相比较，计算出混合模型的预测误差。

3.2 预测误差计算公式

显然，预测精确度是评价各种预测方法的最有效、最重要的标准。因此，本文使用了几种标准去评估混合模型的精确度，包括：方均根误差（RMSE），平均绝对误差（MAE），平均相对百分比误差（MAPE）。其定义分别为

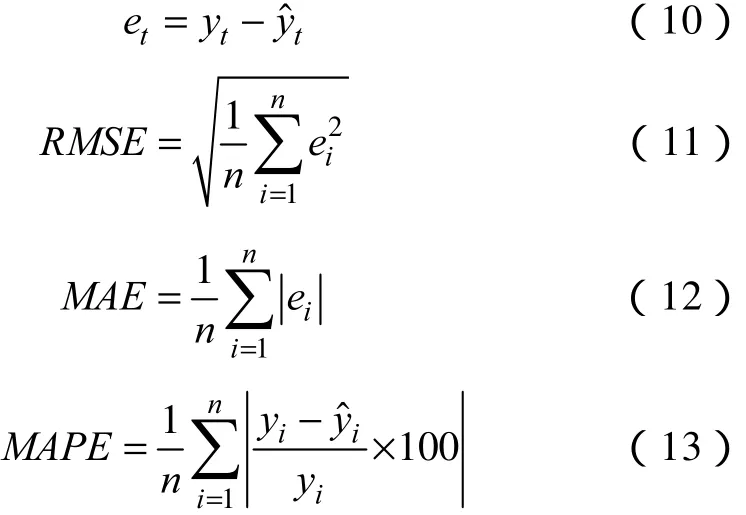
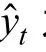
3.3 预测结果

按3.1小节的建模流程，对2011年3月的测风数据建模，并绘制预测曲线如图7所示。

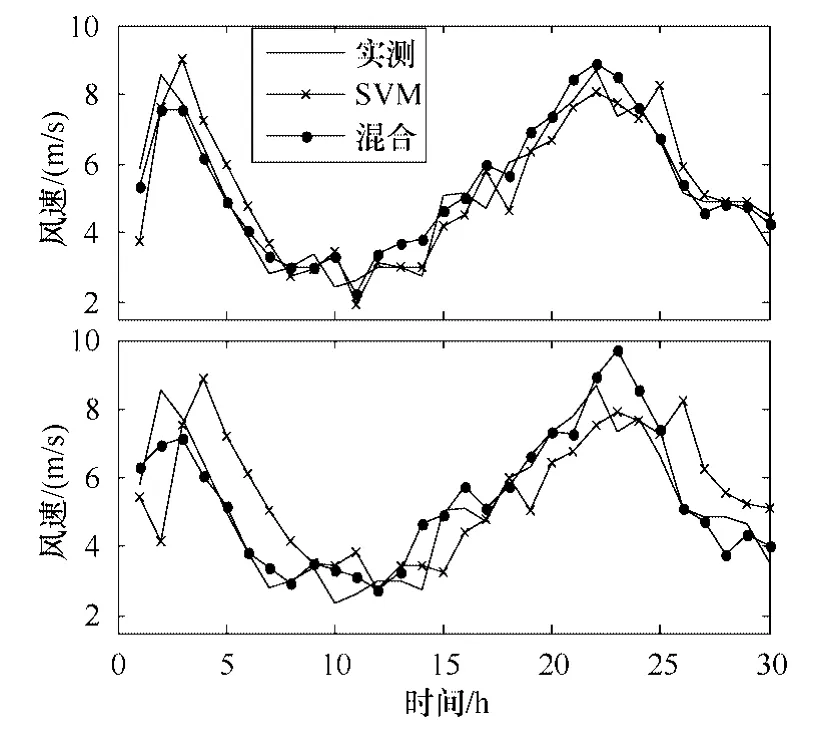
图7 SVM与混合模型的1～2h的风速预测曲线Fig.7 Wind speed forecast curve of SVM and hybrid model

图7中上半部分为1h预测曲线，而下半部分为2h预测曲线。SVM 在基于历史数据的风速预测模型中有着较高的预测精度，故图中将混合模型的预测曲线与SVM的预测曲线相比较。由图 7可以看出，SVM模型的预测值相比实测值有明显的迟滞，而混合模型则在很大程度上消除了此迟滞，能够适时地跟随风速的变化趋势，提高了预测精度。并且，当预测时间增加时，SVM 模型的预测迟滞更加明显，而混合模型则仍能很好地跟随风速实测曲线，显现出更大的优势。

为全面评估混合模型的预测性能，本文同时使用连续法、SVM等经典的预测方法与混合模型对相同的测风数据库进行大量仿真，并比较预测性能。连续法即以当前时刻的风速值作为预测值，是使用最广泛的比较基准；SVM则为近年来应用于风电预测的方法，其预测精度较其他的统计模型有着明显提高。

以使用S1为例（S2同理），具体建模所用数据为：基于测风站点S1、风电场W在2010年全年的测风数据进行模型训练，得到混合模型的参数。之后，以2011年1月至6月的数据为测试集，每个月的抽样时段为连续5天，即进行6次预测：每次连续预测120个点。仿真得到的预测值与实测值对比，按 3.2节中的公式计算得到几种模型的预测误差结果见下表。

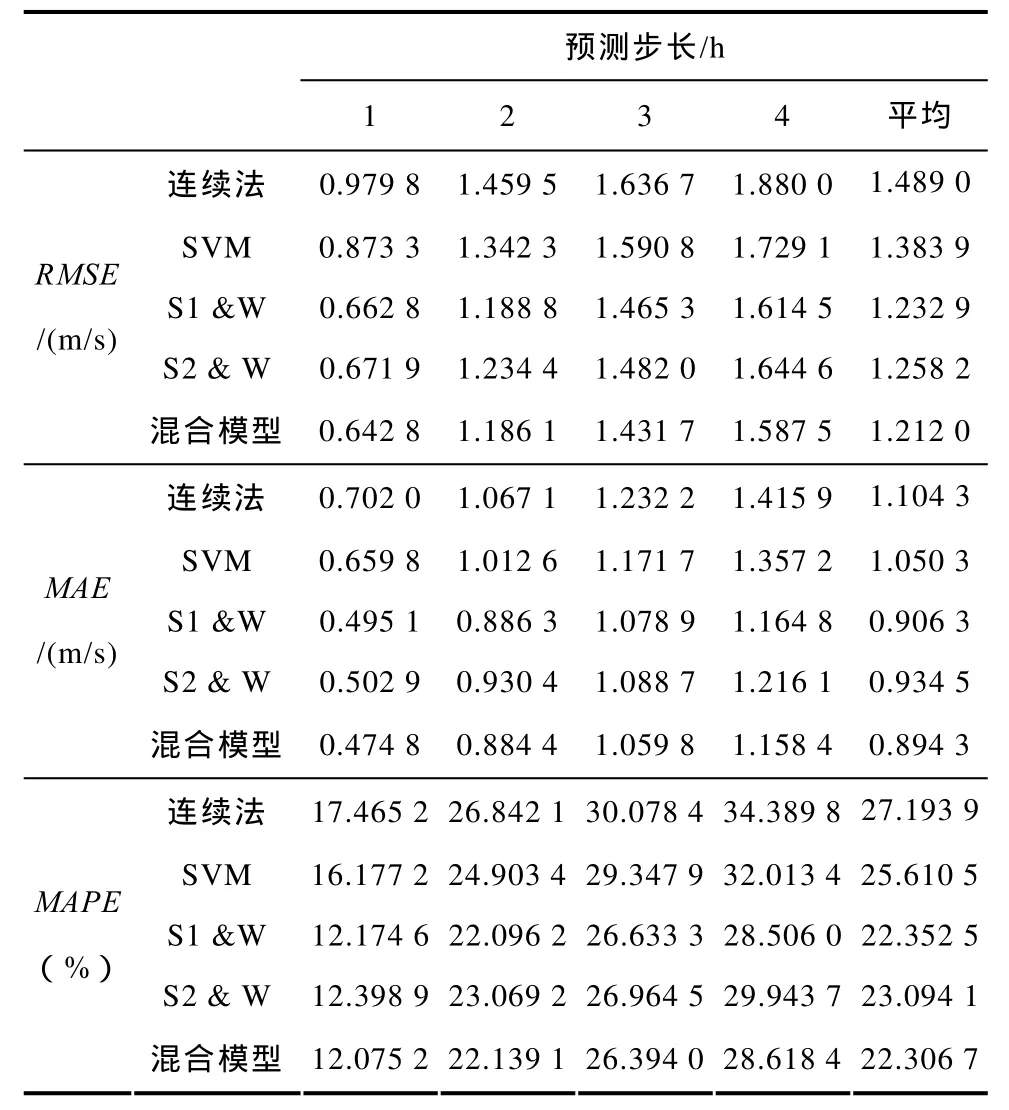
表 预测误差列表Tab. Forecasting error of different models

由以上的误差对比列表中可以看出，相比较其他的单模型来说，本文所提出的空间相关法与支持向量机结合的混合模型，大大提高了预测精度。定义预测精度提高度公式为

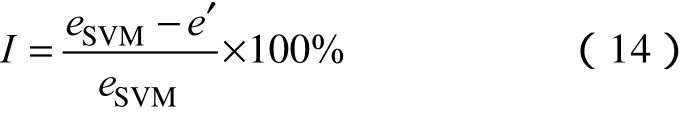
则按RMSE误差值可计算出，与单纯的SVM模型相比较，混合模型的预测精度提高度为：1h预测26.39%，4h预测8.19%，总平均12.42%。

由上文可知，基于历史数据的统计方法，因缺乏地形、气象等物理信息，从根本上难以把握风速未来的变化趋势。而本文提出的混合模型，由于合理加入了风电场周边测风站点的监测数据，可以较好地预测风速的变化趋势。同时，该模型根据风向区间、预测时间分类，实时计算与 SVM 模型相结合的权值系数，在很大程度上避免了当主风向与测风站点所在位置偏离较远时，空间相关模型可能出现的预测误差极值点，使得预测精度更为稳定。计算结果证明，该混合模型的预测精度有了较大提高，具有良好的实用性与可行性。

4 结论

本文首先在详细分析风速空间相关原理的基础上提出了由相关系数极值选择模型输入的判据，并建立了分风向的空间相关模型；再给出基于支持向量机的风速预测模型，之后采用协方差优选权值法将两者结合，得到了新的混合模型，以用于风速的多小时预测。

文中对实测数据的分析计算表明，混合模型由于合理地利用了风电场周边测风站点的监测数据，大幅提高了风速的多小时预测精度（平均预测精度约提高12%），其有效性与可行性得到验证。

考虑到风速的多变性和不可控性，单纯基于历史数据的预测方法效果有限，并且随着预测时间的增长，其预测精度必然会大幅降低。因此，如何合理地将风电场周边的地理、气象信息加入到风电预测模型中，将会是未来研究的热点。

[1] Fan Shu, Liao J R, Yokoyama R, et al. Forecasting the wind generation using a two-stage network based on meteorological information[J]. IEEE Transactions on Energy Conversion, 2009, 24(2): 474-482.

[2] Global Wind Energy Council. Global wind statistics 2011[OL]. http://www.gwec.net/uploads/media/GWECPRstats-2011_20120206_06__1_.pdf

[3] Ma lei, Luan Shiyan, Jiang Chuanwen, et al. A review on the forecasting of wind speed and generated power[J]. Renewable and Sustainable Energy Reviews,2009, 13(4): 915-920.

[4] Alexandre C, Antonio C, Jorge N, et al. A review on the young history of the wind power short-term prediction[J]. Renewable and Sustainable Energy Reviews, 2008, 12(6): 1725-1744.

[5] Ergin Erdem, Jing Shi. ARMA based approaches for forecasting the tuple of wind speed and direction[J].Applied Energy, 2011, 88(4): 1405-1414.

[6] Liu H, Erdem E, Shi J. Comprehensive evaluation of ARMA-GARCH approaches for modeling the mean and volatility of wind speed[J]. Applied Energy, 2011,88(3): 724-732.

[7] P Louka, G Galanis, N Siebert, et al. Improvements in wind speed forecasts for wind power prediction purposes using Kalman filtering[J]. Journal of Wind Engineering and Industrial Aerodynamics, 2008,96(12): 2348-2362.

[8] Erasmo Cadenas, Wilfrido Rivera. Short term wind speed forecasting in La Venta, Oaxaca, Mexico, using artificial neural networks[J]. Renewable Energy, 2009,34(1): 274-278.

[9] 冬雷, 王丽婕, 高爽, 等, 基于混沌时间序列的大型风电场发电功率预测建模与研究[J]. 电工技术学报, 2008, 23(12): 125-129.Dong Lei, Wang Lijie, Gao Shuang, et al. Modeling and analysis of prediction of wind power generation in the large wind farm based on chaotic time series[J].Transactions of China Electrotechnical Society, 2008,23(12): 125-129.

[10] 袁铁江, 晁勤, 李义岩, 等, 大规模风电并网电力系统经济调度中风电场出力的短期预测模型[J]. 中国电机工程学报, 2010, 30(13): 23-27.Yuan Tiejiang, Chao Qin, Li Yiyan, et al. Short-term wind power output forecasting model for economic dispatch of power system incorporating large-scale wind farm[J]. Proceedings of the CSEE, 2010, 30(13):23-27.

[11] Sancho S, Emilio G, Angel M, et al. Short term wind speed prediction based on evolutionary support vector regression algorithms[J]. Expert Systems with Applications, 2011, 38(4): 4052-4057.

[12] 罗文, 王莉娜. 风场短期风速预测研究[J]. 电工技术学报, 2011, 26(7): 68-74.Luo Wen, Wang Lina. Short-term wind speed forecasting for wind farm[J]. Transactions of China Electrotechnical Society, 2011, 26(7): 68-74.

[13] Ignacio J, L. Alfredo, Claudio M, et al. Comparison of two new short-term wind power forecasting systems[J]. Renewable Energy, 2009, 34(7):1848-1854.

[14] Sancho S, Angel M, Emilio G, et al. Hybridizing the fifth generation mesoscale model with artificial neural networks for short-term wind speed prediction[J].Renewable Energy, 2009, 34(6): 1451-1457.

[15] 范高峰, 王伟胜, 刘纯, 等. 基于人工神经网络的风电功率预测[J]. 中国电机工程学报, 2008, 28(34):118-123.Fan Gaofeng, Wang Weisheng, Liu Chun, et al. Wind power prediction based on artificial neural network[J].Proceedings of the CSEE, 2008, 28(34): 118-123.

[16] 李文良, 卫志农, 孙国强, 等. 基于改进空间相关法和径向基神经网络的风电场短期风速分时预测模型[J]. 电力自动化设备, 2009, 29(6): 89-92.Li Wenliang, Wei Zhinong, Sun Guoqiang, et al.Multi-interval wind speed forecast model based on improved spatial correlation and RBF neural network[J]. Electric Power Automation Equipment,2009, 29(6): 89-92.

[17] T G Barbounis, J B Theocharis. Locally recurrent neural networks for wind speed prediction using spatial correlation[J]. Information Sciences, 2007,177(24): 5775-5797.

[18] T G Barbounis, J B Theocharis, M C Alexiadis, et al.Long-term wind speed and power forecasting using local recurrent neural network models[J]. IEEE Transactions on Energy Conversion, 2006, 21(1):273-284.

[19] Gong Li, Jing Shi. On comparing three artificial neural networks for wind speed forecasting[J].Applied Energy, 2010, 87(7): 2313-2320.

[20] Jayadeva, Khemehandani R, Chandra S. Twin support vector machines for pattern classification[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2007, 29(5): 905-910.

[21] Smola A J, Scholkopf B. A tutorial on support vector regression[J]. Statistics and Computing, 1998, 14(3):199-222.